Lista de probleme 3
Nivelul concursului: Național
http://oni2016craiova.ro/ http://www.oni2016.ro/
Grupe
Clasa a V-a Clasa a VI-a Clasa VII-a Clasa VIII-a Clasa a IX-a Clasa a X-a Clasele XI-XII Juniori Seniori
#1702
Cristale
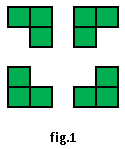 Pietrele preţioase au fascinat omenirea încă din timpuri străvechi iar cele mai renumite dintre ele, cristalele, au devenit atât simbolul durităţii cât şi al eternităţii. În urma unui studiu ştiinţific, pe un eşantion de formă dreptunghiulară se pot observa diferite tipuri de molecule, dispuse într-o geometrie perfectă, pe
Pietrele preţioase au fascinat omenirea încă din timpuri străvechi iar cele mai renumite dintre ele, cristalele, au devenit atât simbolul durităţii cât şi al eternităţii. În urma unui studiu ştiinţific, pe un eşantion de formă dreptunghiulară se pot observa diferite tipuri de molecule, dispuse într-o geometrie perfectă, pe M rânduri a câte N molecule fiecare, aliniate una lângă alta. O formaţiune cristalizabilă este alcătuită din 3 molecule de acelaşi tip, învecinate două câte două, având una dintre cele patru forme din imaginea alăturată (fig.1).
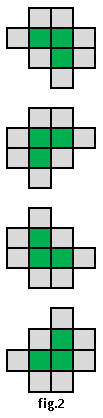 Fiecare formaţiune este înconjurată de jur-împrejur, ca în fig.2, de un înveliş special format şi el din molecule identice, de alt tip decât cele din formaţiunea cristalizabilă pe care o înconjoară şi o izolează de restul formaţiunilor moleculare. În acest fel, fiecare moleculă din formaţiunea cristalizabilă se învecinează la Nord, Sud, Est şi Vest cu o moleculă din aceeaşi formaţiune cristalizabilă sau cu o moleculă din învelişul special.
Fiecare formaţiune este înconjurată de jur-împrejur, ca în fig.2, de un înveliş special format şi el din molecule identice, de alt tip decât cele din formaţiunea cristalizabilă pe care o înconjoară şi o izolează de restul formaţiunilor moleculare. În acest fel, fiecare moleculă din formaţiunea cristalizabilă se învecinează la Nord, Sud, Est şi Vest cu o moleculă din aceeaşi formaţiune cristalizabilă sau cu o moleculă din învelişul special.
Fiecare formaţiune cristalizabilă se bombardează cu raze X şi în acest fel are loc cristalizarea, proces prin care învelişul special se extinde peste formaţiunea cristalizabilă pe care o înconjoară, formând o singură structură din care se va dezvolta cristalul.
Cerințe
- Determinaţi numărul formaţiunilor cristalizabile ce pot fi identificate pe eşantionul analizat.
- Afişaţi eşantionul rezultat după cristalizare.
ONI 2016, clasa a VII-a
- Fișiere
- Cristina Iordaiche
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Probleme diverse
#1701
Birouri
 Arhi şi-a propus să extindă clădirea de birouri pe care a proiectat-o iniţial pe un singur nivel numerotat cu
Arhi şi-a propus să extindă clădirea de birouri pe care a proiectat-o iniţial pe un singur nivel numerotat cu 1, împărţit în n*n zone pătratice de latură 1, fiecare corespunzând unui birou, prin construirea mai multor niveluri. În colţurile tuturor birourilor se construiesc grinzi de rezistenţă. Pentru a asigura rezistenţa întregii clădiri, Arhi va proiecta niveluri noi, numerotate cu 2, 3,… atât timp cât conțin cel puțin un birou și sunt respectate următoarele patru reguli:
- R1: fiecare nivel nou va fi proiectat sub forma unui dreptunghi sau pătrat de arie maximă pentru nivelele cu număr impar, respectiv, sub forma unui pătrat de arie maximă pentru nivelele cu număr par;
- R2: fiecare dintre colţurile zidurilor unui nivel nou trebuie plasat pe câte o grindă de rezistenţă dintre două sau mai multe birouri de pe nivelul precedent;
- R3: oricare două dintre colţurile zidurilor unui nivel nou vor fi plasate pe ziduri diferite (un zid nu se poate suprapune în totalitate pe alt zid) şi cel puţin două vârfuri opuse ale unui nivel nou se vor afla pe ziduri opuse ale nivelului precedent;
- R4: orice porţiune de zid de pe nivelul
k(k>1), construită deasupra unui birou de pe nivelulk-1, se va suprapune exact peste una dintre laturile biroului, sau îl va străbate în diagonală.
Birourile de pe nivelul k (k>1), vor fi construite exact deasupra celor de pe nivelul precedent, astfel, nivelurile 2, 4 etc. vor avea lângă ziduri spaţii triunghiulare care nu vor aparţine niciunui birou.
Numerele inscripţionate pe birouri în imaginea de mai sus, indică nivelul corespunzător birourilor vizibile de deasupra clădirii.
Cunoscându-se lungimea n a laturii primului nivel al clădirii, să se determine:
- numărul maxim de niveluri pe care le poate avea clădirea;
- numărul total de birouri ale clădirii cu număr maxim de niveluri.
ONI 2016, clasa a VII-a
- Fișiere
- Florentina Ungureanu
- concurs
- Clasa 9 Algoritmi elementari Probleme diverse
#1703
Parchet
Meseria de parchetar a devenit mai uşoară de când a apărut parchetul laminat. Acesta se livrează în plăci pătratice de câte 1 m2 şi montarea lui este destul de uşoară. Gigel este convins că este suficient de priceput să facă această operaţie în propria locuinţă. El dispune de planul locuinţei şi a cumpărat o anumită cantitate reprezentând X m2 de parchet laminat. Planul locuinţei este descris printr-un tablou bidimensional de dimensiuni N x M, fiecare element al tabloului reprezentând exact 1 m2. Pereţii sunt reprezentaţi prin caracterul ‘P’ iar suprafeţele camerelor prin caracterul ‘S’ (spaţiu). În planul din figura următoare este descrisă o locuinţă cu 5 camere acestea având respectiv, suprafeţele de 10, 2, 1, 3, 5 m2.
PPPPPPPPP PSSSPSPSP PSSSPSPPP PSSPPPPSP PSPPSSPSP PSPSSSPSP PPPPPPPPP
Gigel nu este sigur de faptul că parchetul cumpărat îi ajunge. Din această cauză a hotărât iniţial să pună parchetul începând cu camera cea mai mare, apoi în următoarea, în ordinea descrescătoare a suprafeţei şi aşa mai departe, până în momentul în care parchetul rămas nu mai este suficient pentru acoperirea suprafeţei următoarei camere. Nu va lăsa neparchetată o cameră pentru a parcheta una cu o suprafaţă mai mică.
Gigel se mai gândeşte şi la posibilitatea de a acoperi complet un număr maxim de camere folosind întreaga cantitate de parchet.
Fiind date N, M, X şi planul locuinţei să se determine:
- numărul
Cde camere pe care a reuşit să le acopere Gigel şi numărulRde m2 de parchet care îi rămân, procedând aşa cum a hotărât iniţial; - numărul de posibilităţi de parchetare a unui număr maxim de camere, folosind întreaga cantitate de parchet.
ONI 2016, clasa a VII-a
- Fișiere
- Marinel Serban
- concurs
- Clasa 10 Probleme diverse Diverse