Triunghiul lui Pascal este un tablou triunghiular cu numere naturale, în care fiecare element aflat pe laturile triunghiului are valoarea 1, iar celelalte elemente sunt egale cu suma celor două elemente vecine, situate pe linia de deasupra.
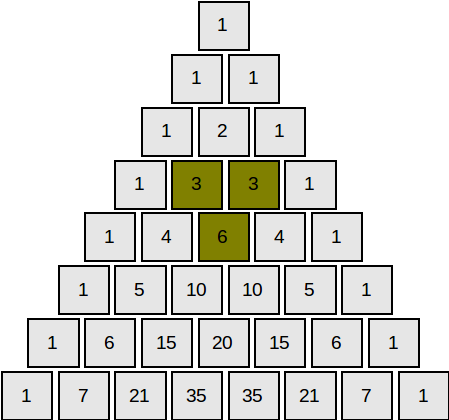
Proprietăți
Putem rearanja elementele tabloului astfel:
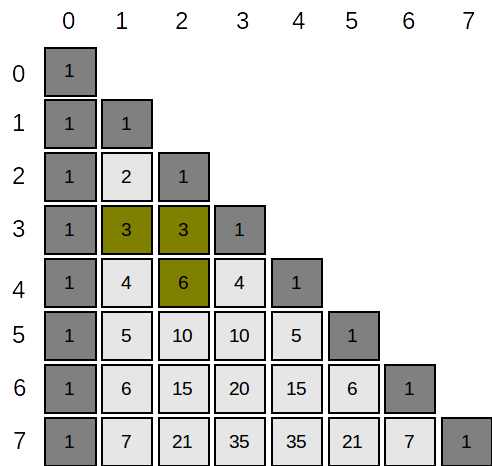
Considerând liniile și coloanele numerotate ca mai sus atunci: \( A_{i,j} = \begin{cases}
1& \text{dacă } i = j \text{ sau } j = 0,\\
A_{i-1,j-1 } + A_{i-1, j} & \text{altfel}.
\end{cases} \). De fapt, această relație este cunoscută în calculul combinărilor: \( {C^{k}_{n}} = \begin{cases}
1& \text{dacă } n = k \text{ sau } k = 0,\\
{ C^{k-1}_{n-1} } + { C^{k}_{n-1} } & \text{altfel}.
\end{cases} \), unde \(C^{k}_{n}\) înseamnă “combinări de n luate câte k”. De fapt, un element \(A_{i,j}\) al tabloului de mai sus este egal cu \( {C^{j}_{i}} \).
Elementele de pe linia n sunt coeficienți binomiali ai dezvoltării \( (a+b)^n = C^{0}_{n} \cdot a^n + C^{1}_{n} \cdot a^{n-1} \cdot b^1 + C^{2}_{n} \cdot a^{n-2} \cdot b^2 + \cdots + C^{k}_{n} \cdot a^{n-k} \cdot b^k + \cdots + C^{n-1}_{n} \cdot a^{1} \cdot b^{n-1} + C^{n}_{n} \cdot b^{n} \) – binomul lui Newton.
Suma elementelor de pe linia n este egală cu 2n: \( {C^{0}_{n}} + {C^{1}_{n}} + {C^{2}_{n}} + \cdots + {C^{k}_{n}} + \cdots + {C^{n}_{n}} = 2^n \).

Problemă
Se citește un număr natural n. Afișați linia n din triunghiul lui Pascal.
Soluție cu combinări
O primă soluție constă în calcularea valorii \( C^{k}_{n} \) pentru fiecare \( k \in \left\{0, 1, 2, \cdots , \ n \right\} \).
#include <iostream>
using namespace std;
int comb(int n , int k)
{
int p = 1;
for(int i = 1 ; i <= k ; i ++)
p = p * (n-i+1) / i;
return p;
}
int main()
{
int n;
cin >> n;
for(int i = 0 ; i <= n ; i ++)
cout << comb(n,i) << " ";
return 0;
}
O îmbunătățire a variantei de mai sus este:
#include <iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int p = 1;
cout << "1 ";
for(int i = 1 ; i <= n ; i ++)
{
p = p * (n-i+1) / i;
cout << p << " ";
}
return 0;
}
Soluție cu matrice
În soluția următoare aplicăm formula \( A_{i,j} = A_{i-1,j-1 } + A_{i-1, j} \), folosind un tablou unidimensional:
#include <iostream>
using namespace std;
int main()
{
int n, A[31][31];
cin >> n;
for(int i = 0 ; i <= n ; i ++)
{
A[i][0] = A[i][i] = 1;
for(int j = 1 ; j < i ; j ++)
A[i][j] = A[i-1][j-1] + A[i-1][j];
}
for(int j = 0 ; j <= n ; j ++)
cout << A[n][j] << " ";
return 0;
}
Soluție cu doi vectori
Soluția de mai sus poate fi îmbunătățită, observând că pentru a calcula linia curentă folosim doar linia precedentă. Vom folosi doar doi vectori, unul pentru linia curentă, celălalt pentru linia precedentă:
#include <iostream>
using namespace std;
int main()
{
int n, v[31],u[31];
cin >> n;
v[0] = 0;
for(int i = 1 ; i <= n ; i ++)
{
u[0] = u[i] = 1;
for(int j = 1 ; j < i ; j ++)
u[j] = v[j-1] + v[j];
for(int j = 0 ; j <= i ; j ++)
v[j] = u[j];
}
for(int j = 0 ; j <= n ; j ++)
cout << v[j] << " ";
return 0;
}
Soluție cu doi vectori și doi pointeri
În soluția de mai sus putem evita copierea elementelor din u în v, folosind doi pointeri suplimentari. Aceștia vor memora adresa de început a celor două tablouri, iar copierea elementelor este înlocuită de interschimbarea valorilor celor doi pointeri:
#include <iostream>
using namespace std;
int main()
{
int n, A[31], B[31];
int * u = A, * v = B;
cin >> n;
v[0] = 0;
for(int i = 1 ; i <= n ; i ++)
{
u[0] = u[i] = 1;
for(int j = 1 ; j < i ; j ++)
u[j] = v[j-1] + v[j];
swap(u,v);
}
for(int j = 0 ; j <= n ; j ++)
cout << v[j] << " ";
return 0;
}
Soluție cu un singur vector
Putem folosi un singur vector. Acesta conține linia anterioară și se modifică pas cu pas, pentru a deveni linia curentă a triunghiului:
#include <iostream>
using namespace std;
int main()
{
int n, v[31];
cin >> n;
v[0] = 0;
for(int i = 1 ; i <= n ; i ++)
{
v[i] = 1;
for(int j = i - 1 ; j > 0 ; j --)
v[j] = v[j] + v[j-1];
v[0] = 1;
}
for(int j = 0 ; j <= n ; j ++)
cout << v[j] << " ";
return 0;
}