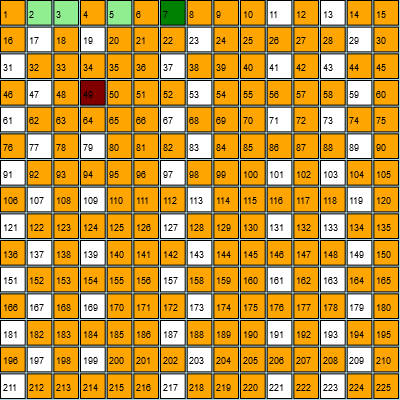
Introducere
Ciurul lui Eratostene reprezintă o metodă de determinare a tuturor numerelor prime mai mici sau egale cu o valoare dată, n. În practică, valoarea lui n trebuie să fie una rezonabilă, ea depinzând de restricțiile de timp și memorie aplicate problemei.
Ciurului Eratostene se aplică în felul următor – în continuare lucrăm cu n=30:
- se scriu toate numerele naturale de la
1lan=30:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- se taie din lista numărul
1, care nu este prim
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- se identifică următorul număr netăiat,
2. Acest este prim, iar din listă se vor tăia toți multipli săi, mai mari decât acesta.
| 2 | 3 | 5 | 7 | 9 | |||||
| 11 | 13 | 15 | 17 | 19 | |||||
| 21 | 23 | 25 | 27 | 29 |
- se identifică următorul număr netăiat,
3. Acest este prim, iar din listă se vor tăia toți multipli săi, mai mari decât acesta. Unii dintre ei au fost deja tăiați, deoarece sunt și multipli ai lui2.
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 17 | 19 | ||||||
| 23 | 25 | 29 |
- se identifică următorul număr netăiat,
5. Acest este prim, iar din listă se vor tăia toți multipli săi, mai mari decât acesta. Unii dintre ei au fost deja tăiați, deoarece sunt și multipli ai lui2sau3.
| 2 | 3 | 5 | 7 | ||||||
| 11 | 13 | 17 | 19 | ||||||
| 23 | 29 |
- se identifică următorul număr netăiat,
7. Acesta este prim, dar totodată7*7>30căutarea numerelor prime s-a încheiat. Toate numerele care nu au fost tăiate sunt prime.
Animație
Algoritm
Pentru identificarea numerelor prime într-un algoritm/program, vom folosi un vector caracteristic, v[], cu următoarea semnificație:
\( v[x]=\begin{cases} 0& \text{dacă $x$ prim},\\1& \text{dacă $x$ nu este prim}.\end{cases} \)
Vom porni de la un vector cu toate elementele nule, apoi vom marca pe rând cu 1 toate numerele care sunt multipli ai unor numere mai mici. Un algoritm pseudocod care realizează acest operații este:
pentru i←0,n execută
V[i] ← 0
sf_pentru
V[0] ← 1
V[1] ← 1
pentru i ← 2,sqrt(n) execută
dacă V[i] = 0 atunci
pentru j ← 2, [n/i] execută
V[i*j] ← 1
sf_pentru
sf_dacă
sf_pentru
Probleme similare
Mecanismul prin care se identifică numerele prime specific Ciurului lui Eraostene poate fi folosit și la determinarea altor rezultate. De exemplu, vrem să aflăm pentru un n dat (nu prea mare) câți divizori are fiecare număr natural din intervalul [1,n].
Pentru acesta, vom construi un vector V, în care v[x] reprezintă numărul de divizori ai lui x. Pentru a construi acest vector, vom parcurge numerele de la 1 la n, și pentru fiecare număr x vom identifica multiplii săi. Pentru fiecare y multiplu al lui x vom incrementa valoarea lui v[y].
Un algoritm pseudocod este:
pentru i←1,n execută
V[i] ← 0
sf_pentru
pentru x ← 1,n execută
pentru y ← x, n , x execută
V[y] ← V[y] + 1
sf_pentru
sf_pentru
Probleme ataşate
| Nr. | Problema | Clasa | Dificultate | Operații I/O |
|---|---|---|---|---|
| 1 | #0303 - Eratostene | 9 | medie | fișiere |
| 2 | #1394 - devt | 9 | dificilă | fișiere |
| 3 | #1822 - Artificii | 9 | concurs | fișiere |
| 4 | #1145 - Extraprime | 9 | concurs | fișiere |
| 5 | #2175 - Factori | 9 | concurs | fișiere |
| 6 | #1931 - Fantastice | 9 | concurs | fișiere |
| 7 | #1673 - Cmmdc1 | 9 | concurs | fișiere |
| 8 | #1916 - Catalin si greselile | 11 | concurs | fișiere |
| 9 | #2148 - ADN | 9 | concurs | fișiere |
| 10 | #3227 - Tramvaie | 9 | concurs | fișiere |
| 11 | #3313 - Eratostene2 | 9 | medie | fișiere |
| 12 | #3301 - nrdiv9 | 9 | medie | fișiere |