Algoritmul lui Dijkstra determină pentru un nod dat într-un graf orientat cu costuri costurile minime ale drumurilor care au acel nod ca extremitate inițială.
Mai precis, pentru un nod s – sursă, algoritmul determină pentru orice nod x costul minim al unui drum de la s la x.
Strategia algoritmului lui Dijkstra este una de tip Greedy:
- se menține un tablou
d[], în cared[x]reprezintă costul minim curent (eventual infinit) al unui drum de laslax; - se menține o mulțime
Fde nodurikpentru care s-a determinat costul minim finald[k] - inițial în
Fse adaugă doar noduls, pentru cared[s]=0; pentru nodurilexadiacente cus,d[x]=c[s,x], undec[x,y]este costul arcului(x,y), iar pentru celelalte noduri costuld[]se inițializează cu INFINIT; - în mod repetat:
- alegem un nod din afara mulțimii
F, nodulkpentru care costul drumuluid[k]este minim și finit; - adăugăm nodul găsit
kînF; - pentru fiecare arc
(k,x)cuxdin afara mulțimiiFstabilim dacă acest arc se îmbunătățește costuld[x](arcul relaxează drumul);
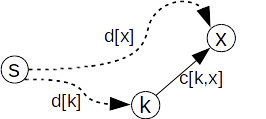
- alegem un nod din afara mulțimii
- alegerea acestor noduri se termină când toate nodurile au fost adăugate în
F(s-au determinat costurile drumurile de lasla fiecare nod al grafului) sau când nu mai există nodurixdin afara mulțimiiFpentru cared[x]este finit;
Exercițiu
Aplicați algoritmul lui Dijkstra pentru graful de mai jos și s=1:
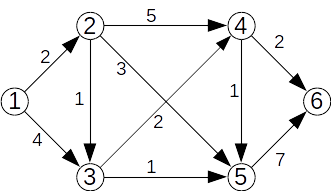
Secvență C++
În secvența de mai jos, considerăm un garf orientat cu în noduri, reprezentat prin matricea de adiacență a[][], în care a[i][j]=INFINIT dacă nu există arcul (i,j).
#define INFINIT 1000000000
...
//nodul sursa este s
...
for(i =1 ; i <= n ; i ++ )
{
f[i] = 0;
d[i] = a[s][i];
}
f[s] = 1, d[s] = 0;
d[0] = INFINIT; // pentru determinarea nodului cu costul minim
for(int k = 1 ; k < n ; ++k)
{
int pmax = 0;
for(i = 1 ; i <= n ; ++i)
if(f[i] == 0 && d[i] < d[pmax])
pmax = i;
if(pmax > -1)
{
f[pmax] = 1;
for(i = 1; i <= n ; ++i)
if(f[i] == 0 && d[i] > d[pmax] + a[pmax][i])
d[i] = d[pmax] + a[pmax][i];
}
}Citește mai departe