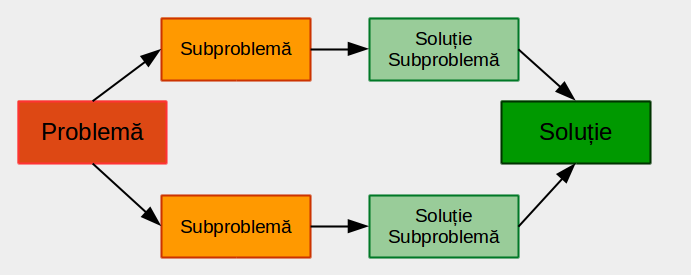
Divide et Impera este o metodă de programare bazată pe un principiu simplu:
- problema dată se descompune în două (sau mai multe) subprobleme (de același tip ca problema inițială, dar de dimensiuni mai mici);
- se rezolvă independent fiecare subproblemă;
- se combină rezultatele obținute pentru subprobleme, obținând rezultatul problemei inițiale.
Subproblemele trebuie să fie de același tip cu problema inițială, ele urmând a fi rezolvate prin aceeași tehnică.
Subproblemele în care se descompun problema dată trebuie să fie:
- de același tip cu problema dată;
- de dimensiuni mai mici (mai “ușoare”);
- independente (să nu se suprapună, prelucrează seturi de date distincte).
În tehnica Divide et Impera, în urma împărțirilor succesive în subprobleme, se ajunge în situația că problema curentă nu mai poate fi împărțită în subprobleme. O asemenea problemă se numește problemă elementară și se rezolvă în alt mod – de regulă foarte simplu.
Divide et Impera admite de regulă o implementare recursivă – rezolvarea problemei constă în rezolvarea unor subprobleme de același tip. Un algoritm pseudocod care descrie metoda este:
Algoritm DivImp(P)
Dacă P este problemă elementară
R <- RezolvăDirect(P)
Altfel
[P1,P2] <- Descompune(P)
R1 <- DivImp(P1)
R2 <- DivImp(P2)
R <- Combină(R1,R2)
SfârșitDacă
SfârșitAlgoritm
Aplicații
Suma elementelor dintr-un vector
Fie un vector V cu n elemente întregi, indexate de la 1 la n. Să se determine suma lor.
Problema este binecunoscută. Cum o rezolvăm prin metoda Divide et Impera? Care sunt subproblemele?
A împărți problema în subprobleme constă de fapt în a împărți vectorul în doi subvectori, cu număr (aproape) egal de elemente. Primul subvector ar fi V cu elementele indexate de la 1 la n/2 (prima jumătate a lui V), iar al doilea ar fi a doua jumătate – elementele indexate de la n/2+1 la n.
Prima jumătate este un vector, dar a jumătate nu mai este un vector, elementele nu mai sunt indexate de la 1 la ..., deci cele două subprobleme nu mai sunt de același tip (sau cel puțin nu în mod direct).
Putem reformula problema inițială astfel:
Fie un vector V cu n elemente întregi, indexate de la 1 la n. Determinați suma elementelor din secvență delimitată de indicii 1 și n.
Vom realiza o funcție care să determine pentru vectorul V suma elementelor din secvența delimitată de indicii st și dr. Pentru a rezolva problema dată vom apela funcția cu parametrii st=1 și dr=n. Această abordare are două avantaje:
- putem rezolva problema prin metoda divide et impera – o secvență poate fi împărțită în alte după secvențe, de dimensiuni mai mici;
- putem folosi funcția realizată pentru a determina suma elementelor din orice secvența a vectorului.
Pentru secvența delimitată de st și dr, procedăm astfel:
- dacă
st == dr, atunci suma esteV[st]; - altfel:
- împărțim problema în subprobleme: determinăm mijlocul secvenței,
m = (st + dr) / 2; astfel, obținem două secvențe: prima conține elementele cu indici întrestșim, iar a doua conține elementele cu indici întrem+1șidr(observăm că cele două secvențe nu au elemente comune – subproblemele sunt independente); - rezolvăm cele două subprobleme în același mod:
- determinăm
S1 =suma din prima secvență - determinăm
S2 =suma din a doua secvență;
- determinăm
- combinăm rezultatele: suma pe secvența inițială este egală cu
S1 + S2.
- împărțim problema în subprobleme: determinăm mijlocul secvenței,
Secvență C++:
int Suma(int V[], int st, int dr)
{
if(st == dr)
return V[st]; // problemă elementară
else
{
int m = (st + dr) / 2; // împărțim problema în subprobleme
int s1 = Suma(V, st, m); // rezolvăm prima subproblemă
int s2 = Suma(V, m + 1, dr); // rezolvăm a doua subproblemă
return s1 + s2; // combinăm rezultatele
}
}
int main()
{
int V[101], n;
//citire n si V
cout << Suma(V,1,n);
return 0;
}
Cmmdc al elementelor dintr-un vector
Fie un vector V cu n elemente naturale nenule, indexate de la 1 la n. Să se determine cel mai mare divizor comun al lor.
La fel în cazul problemei precedente, o transformă într-una cu secvențe. Vom determina cel mai mare divizor comun al elementelor dintr-o secvență delimitată de indicii st și dr.
CMMDC(V,st,dr):
- dacă secvența este formată dintr-un singur element (
st == dr), atunci rezultatul este chiarV[st]; - altfel:
- determinăm indicele de la mijloc,
m = (st + dr) / 2; - determinăm recursiv
a = CMMDC(V, st, m); - determinăm recursiv
b = CMMDC(V, m + 1, dr); - rezultatul este
Cmmdc2(a,b), undeCmmdc2(x,y)este cel mai mare divizor comun a luixșiy, și poate fi determinat cu algoritmul lui Euclid.
- determinăm indicele de la mijloc,