QuickSort sau Sortarea rapidă este o metodă eficientă de sortare a unui tablou, descoperită în 1960 de programatorul britanic C.A.R. Hoare. Pentru un set de n valori oarecare algoritmul efectuează \( O(n \log n) \) comparații, dar în cazul cel mai nefavorabil se efectuează \( O(n^2) \) comparații.
Algoritmul este de tip divide et impera; el sortează o secvență a tabloului (inițial întreg tabloul), astfel:
- se alege un element special al listei, numit pivot;
- se ordonează elementele listei, astfel încât toate elementele din stânga pivotului să fie mai mici sau egale cu acesta, și toate elementele din dreapta pivotului să fie mai mari sau egale cu acesta;
- se continuă recursiv cu secvența din stânga pivotului și cu cea din dreapta lui.
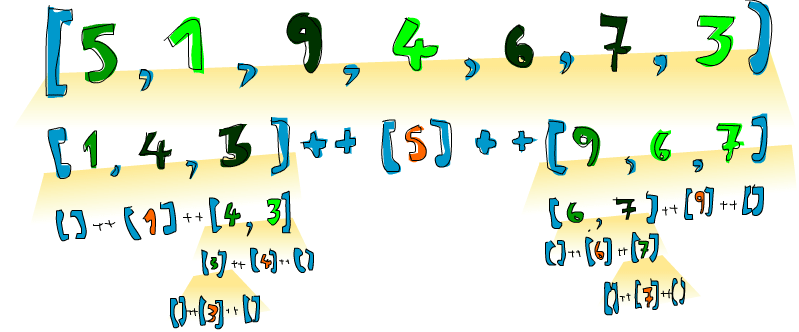
Următoarea funcție C++ realizează sortarea unui tablou, transmis ca parametru:
void QuickSort(int v[], int st, int dr)
{
if(st < dr)
{
//pivotul este inițial v[st]
int m = (st + dr) / 2;
int aux = v[st];
v[st] = v[m];
v[m] = aux;
int i = st , j = dr, d = 0;
while(i < j)
{
if(v[i] > v[j])
{
aux = v[i];
v[i] = v[j];
v[j] = aux;
d = 1 - d;
}
i += d;
j -= 1 - d;
}
QuickSort(v, st , i - 1);
QuickSort(v, i + 1 , dr);
}
}
Observații:
- în timpul pivotării:
- la fiecare iterație, doar una dintre variabilele
ișijse modifică: sau creștei, sau scadej - pivotul este elementul cu indicele care nu se modifică
- la fiecare iterație, doar una dintre variabilele
- algoritmul descris mai sus realizează ordonarea crescătoare a tabloului; pentru ordonarea descrescătoarea algoritmul este asemănător: prin pivotare, elementele din stânga pivotului devin mai mari decât acesta, cele din dreapta devin mai mici;
- algoritmul este cu atât mai rapid cu cât la fiecare etapă cele două secvențe delimitate de pivot au lungimi cât mai apropiate (ideal egale);
- dacă tabloul este de a început ordonat crescător sau descrescător, complexitatea algoritmului devine pătratică – \( O(n^2) \);
- anumite metode de alegere a pivotului pot să evite această situație