Definiții
Un număr natural \( p>1 \) se numește prim dacă:
$$ p \vert ab \Rightarrow p \vert a \text{ sau } p \vert b $$
Un număr natural \( p>1 \) se numește indecompozabil (sau ireductibil) dacă:
$$ d \vert p \Rightarrow d = 1 \text{ sau } d = p $$
Observații
- Pentru orice număr natural \( p>1 \), \( p \) este prim dacă și numai dacă este indecompozabil.
- Cei doi divizori ai unui număr indecompozabil (prim)sunt
1și însuși numărul. - Conform definiției, numerele
0și1nu sunt prime! - Un număr natural mai mare decât
1care nu este prim se numește compus sau decompozabil sau reductibil.
Verificarea primalității
Pentru a stabili dacă un număr p este prim:
- numărăm divizorii săi. Dacă sunt
2divizori,peste prim. - determinăm suma divizorilor. Dacă suma este
p + 1, numărul este prim. - căutăm divizori ai săi diferiți de
1și de el însuși. Dacă nu găsim, numărul este prim.
Cum verificăm algoritmic dacă un număr natural n este prim?
- presupunem că numărul este prim;
- verificăm cazurile particulare; dacă
neste0sau1, schimbăm presupunerea - căutăm un divizor în intervalul \( [2 , \sqrt{n}] \), parcurgând numerele din interval
- dacă îl găsim, schimbăm presupunerea
Observație: Deoarece divizorii unui număr n sunt în pereche, dacă nu găsim divizor în intervalul \( [2 , \sqrt{n}] \), nu vom găsi nici în intervalul \( [\sqrt{n} , n) \).
Blockly:
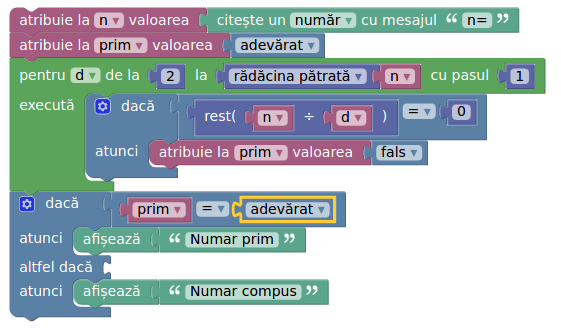
Program C++:
#include <iostream>
int main()
{
int n;
std :: cin >> n;
bool prim = true; // presupunem ca n este prim
if(n < 2)
prim = false; // 0 si 1 nu sunt prime
for(int d =2 ; d * d <= n ; d ++)
if(n % d == 0)
prim = false;
if(prim)
std :: cout << n << " este prim";
else
std :: cout << n << " nu este prim";
return 0;
}