Exerciții
Rezultate 1219
Exercițiul #355
Se consideră un graf neorientat G cu 101 noduri şi 101 muchii. Numărul maxim de vârfuri izolate ale grafului poate fi:
| Varianta 1 |
0 |
| Varianta 2 |
10 |
| Varianta 3 |
50 |
| Varianta 4 |
86 |
Exercițiul #357
Care dintre următoarele perechi (x,y) completează tabelul de mai jos, conținând gradele interioare și exterioare ale unui graf orientat cu 4 noduri.
| vărful | 1 | 2 | 3 | 4 |
| gradul exterior | 2 | 0 | 2 | x |
| gradul interior | 0 | 2 | y | 1 |
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #359
Care este vectorul de ”taţi” corespunzător arborelui cu rădăcină, cu 8 noduri, numerotate de la 1 la 8, dat prin lista următoare a descendenţilor direcţi (fiilor)?
1: 4,6,7 2: - 3: 1,8 4: - 5: - 6: 2 7: - 8: 5
Scrieți elementele vectorului în ordine, separate prin exact un spațiu.
Exercițiul #360
Care este numărul minim de noduri ce trebuie eliminate din graful următor astfel încât subgraful obţinut să nu fie conex?
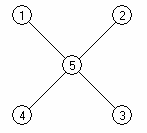
| Varianta 1 |
3 |
| Varianta 2 |
0 |
| Varianta 3 |
2 |
| Varianta 4 |
1 |
Exercițiul #363
Care dintre nodurile grafului neorientat cu 5 noduri, numerotate de la 1 la 5, dat prin matricea de adiacenţă următoare, are gradul cel mai mare?
0 1 1 0 0 1 0 1 0 1 1 1 0 1 1 0 0 1 0 1 0 1 1 1 0
| Varianta 1 |
4 |
| Varianta 2 |
3 |
| Varianta 3 |
5 |
| Varianta 4 |
2 |
Exercițiul #364
Câte valori nule pot să apară într-un vector cu legături „de tip tată” asociat unui arbore cu rădăcină care conţine 10 noduri?
| Varianta 1 |
niciuna |
| Varianta 2 |
exact una |
| Varianta 3 |
exact două |
| Varianta 4 |
depinde de configuraţia arborelui |
Exercițiul #366
Care este numărul maxim de valori egale care pot să apară într-un vector cu legături „de tip tată” asociat unui arbore cu rădăcină care conţine 10 noduri?
| Varianta 1 |
cel mult |
| Varianta 2 |
|
| Varianta 3 |
nu pot să apară valori egale într-un vector cu legături de tip tată |
| Varianta 4 |
|
Exercițiul #368
Se consideră un graf neorientat 5 noduri şi 3 muchii. Care este numărul maxim de noduri cu grad 1 care pot exista în graf?
| Varianta 1 |
2 |
| Varianta 2 |
3 |
| Varianta 3 |
4 |
| Varianta 4 |
5 |
Exercițiul #369
Se consideră un arbore cu rădăcină memorat cu ajutorul vectorului de ”taţi” T=(2,0,1,1,1,2). Stabiliţi care dintre nodurile arborelui sunt situate pe nivelul 3, dacă rădăcina este situată pe nivelul 1?
| Varianta 1 |
3 4 5 |
| Varianta 2 |
1 |
| Varianta 3 |
2 6 |
| Varianta 4 |
1 2 6 |
Exercițiul #371
Fie graful orientat G cu 5 vârfuri, numerotate cu 1, 2, 3, 4, 5, şi arcele (1,2), (1,3), (1,4), (2,3), (4,2), (4,5), (5,2), (2,4). Care dintre următoarele vârfuri au gradul extern egal cu gradul intern?
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|