Lista de probleme 974
Filtrare
#2582
SecvElim
Se dă un șir de caractere care conține doar litere mici și mari ale alfabetului englez. Se parcurge șirul de la stânga la dreapta și dacă se întâlnește o secvență de litere alăturate egale, se șterge. Dacă în urma acestei operații se obține o nouă secvență de litere egale, se șterge și ea, ș. a. m. d.
Să se afișeze șirul obținut.
- Consola
- Mirela Mlisan, Andrei Visalon
- ușoară
- Clasa 10 Şiruri de caractere Prelucrări elementare pe șiruri de caractere
#893
Cuvinte0
Se dă un șir de caractere format din cuvinte, separate prin spații. Cuvintele conțin doar litere mici ale alfabetului englez. Afișați, în ordine lexicografică, cuvintele distincte din șir.
- Consola
- ușoară
- Clasa 10 Şiruri de caractere Probleme diverse
#900
OrdonareF1
C++
Scrieţi definiția completă a subprogramului C++ ordonare care are 2 parametri: a, prin care primeşte un tablou unidimensional cu maximum 1000 de numere naturale mai mici decât 1.000.000.000 și n, numărul efectiv de elemente ale tabloului.
Subprogramul ordonează descrescător elementele tabloului a, fără a returna valori.
#957
Zana
Castelul Zânei Spiriduşilor este construit pe o suprafaţă dreptunghiulară având n*m camere identice, de formă pătratică, dispuse câte m pe direcţia Ox şi câte n pe direcţia Oy ca în desenul de mai jos în care n=3 şi m=6. Din fiecare cameră se poate intra în orice cameră învecinată, cameră care are un perete comun cu acesta. Fiecare cameră este identificată prin coordonatele sale, ca în figură.
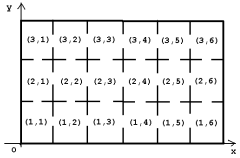
În castel, trăiesc k spiriduşi împreună cu Zâna lor. Fiind în curând aniversarea zilei de naştere a Zânei, fiecare spiriduş a pregătit câte un cadou pe care îl ascunde, nevăzut de ceilalţi, într-una din camerele castelului. Tradiţia acestei sărbătoriri, impune următoarele reguli:
- În căutarea cadourilor, Zâna porneşte din camera de coordonate
(1,1). Ea se deplasează prin camerele castelului cât timp în aceste camere nu se află niciun cadou. - Căutarea se încheie în momentul în care Zâna intră într-o cameră în care se află cel puţin un cadou. Zână va primi toate cadourile aflate în acestă cameră, restul cadourilor vor dispărea.
Scrieţi un program care să citească din fişierul zana.in numerele naturale n, m, k şi cele k coordonatele ale camerelor în care spiriduşii au ascuns cadourile, şi care să determine:
a) numărul n1 maxim de cadouri pe care le poate primi Zâna în urma respectării regulilor;
b) numărului n2 al camerelor în care poate ajunge Zâna respectând regulile, camere ce conţin fiecare câte n1 cadouri.
Olimpiada de Informatică, etapa pe sector, Bucureşti, 2010
- Fișiere
- Carmen Minca
- concurs
- Clasa 10 Recursivitate Probleme diverse
- Fill
#1539
apartenenta
C++
Scrieţi în limbajul C/C++ definiţia completă a subprogramului apartenenta, care primeşte ca argument un număr natural nenul n şi returnează valoarea 1 dacă n aparţine mulţimii \(\scriptsize H = \{ 2^x \cdot 3^y \cdot 5^z \, | \, x, y, z \in N \}\), respectiv 0 în caz contrar.
#1845
OrdonareF_Rec
C++
Scrieţi definiția completă a subprogramului C++ recursiv ordonare care are 2 parametri: a, prin care primeşte un tablou unidimensional cu maximum 1000 de numere naturale mai mici decât 1.000.000.000 și n, numărul efectiv de elemente ale tabloului.
Subprogramul ordonează crescător elementele tabloului a, fără a returna valori.
- Consola
- ușoară
- Clasa 10 Recursivitate Subprograme recursive
#2682
LungimeRandMax
Se citeste un număr natural l și un șir de cel mult 10000 de caractere ce conține cuvinte despărțite între ele prin cate un spațiu. Fiecare cuvânt din șirul de caractere citit este format din cel mult l litere mari ale alfabetului englez. Să se scrie un program care afișează aceste cuvinte, în ordinea în care se citesc, pe linii de cel mult l caractere, astfel încât orice linie începe și se termină cu un cuvânt și oricare două cuvinte de pe aceeași linie sunt separate printr-un singur spațiu. Oricare linie este folosită la maxim, adică dacă un cuvânt are loc pe acea linie va fi pus acolo și nu va fi trecut pe linia următoare sau spart pe 2 linii.
Admitere UNIBUC 2018
#1458
ecuatii_grad_2
Dându-se o ecuaţie de gradul 2, să se scrie un program care determină soluţiile acestei ecuaţii.
- Fișiere
- Alexandru Antal
- medie
- Clasa 10 Şiruri de caractere Probleme diverse
#1846
OrdonareSecvF_REC
C++
Scrieţi definiția completă a subprogramului C++ recursiv ordonare care are 4 parametri: a, prin care primeşte un tablou unidimensional cu maximum 1000 de numere naturale mai mici decât 1.000.000.000 și n, numărul efectiv de elemente ale tabloului și doi indici st dr.
Subprogramul ordonează crescător elementele tabloului a cu indici între st și dr, inclusiv aceștia,fără a modifica celelalte elemente ale tabloului.
- Consola
- ușoară
- Clasa 10 Recursivitate Subprograme recursive
#3257
cifre_romane1
Dan vrea să transforme un număr scris cu cifre romane într-un număr scris cu cifre arabe.
proprie
- Fișiere
- Traian Florian Alin Moldoveanu
- medie
- Clasa 10 Şiruri de caractere Prelucrări elementare pe șiruri de caractere