Lista de probleme 1991

Considerăm un şir de numere a1, a2, …, aN. O secvenţă nevidă în acest şir este de forma ai, ai+1, …, aj, unde i ≤ j. De exemplu, pentru N=4 şi şirul 2 3 4 3, secvenţele nevide sunt: 2, 2 3, 2 3 4, 2 3 4 3, 3, 3 4, 3 4 3, 4, 4 3, 3. Definim puterea unui element ai ca fiind numărul de secvenţe care-l conţin pe ai şi în care ai este strict mai mare decât celelalte elemente ale fiecăreia dintre respectivele secvenţe. Astfel în şirul 2 3 4 3 puterea elementului a1 este 1 (fiind maxim doar în secvenţa formată din el însuşi), a elementului a2 este 2 (a2 fiind maxim în secvenţele 2 3 şi 3), a elementului a3 este 6 (fiind maxim în secvenţele 2 3 4, 2 3 4 3, 3 4, 3 4 3, 4 şi 4 3), iar a elementului a este 1.

Scrieţi un program care determină puterea cea mai mare a unui element din şirul dat, precum şi numărul de elemente din şir care au cea mai mare putere.

Ana şi Bogdan au inventat jocul “Compar”. Ana scrie pe tablă o secvenţă formată din N numere naturale distincte cuprinse între 1 şi N, apoi compară fiecare două numere învecinate din secvenţă scriind între ele semnul < sau semnul >, după caz.
De exemplu, dacă secvenţa de pe tablă este 6 4 2 1 3 5, după compararea elementelor învecinate şi inserarea semnelor în secvenţă, Ana obţine:
6>4>2>1<3<5
După aceea Ana şterge cele N elemente ale secvenţei şi păstrează numai semnele, astfel:
>>><<
La final, Ana îi arată lui Bogdan şirul semnelor şi îi cere să reconstituie secvenţa de numere naturale scrisă iniţial pe tablă.

Cunoscând şirul semnelor construit de Ana, scrieţi un program care să îl ajute pe Bogdan să reconstituie secvenţa de numere naturale distincte scrisă iniţial pe tablă.

După ce au descoperit ascunzătoarea piratului Spânu, marinarii de pe corabia “Speranţa” au hotărât să ofere sătenilor o parte din comoara acestuia. Întrucât comoara avea un număr nelimitat de bani din aur, numiţi galbeni, singura problemă a marinarilor a fost regula după care să împartă banii.

După îndelungi discuţii au procedat astfel: i-au rugat pe săteni să se aşeze în ordine la coadă şi să vină, pe rând, unul câte unul pentru a-şi ridica galbenii cuveniţi. Primul sătean a fost rugat să îşi aleagă numărul de galbeni, cu condiţia ca acest număr să fie format din exact K cifre. Al doilea sătean va primi un număr de galbeni calculat astfel: se înmulţeşte numărul de galbeni ai primului sătean cu toate cifrele nenule ale acelui număr, rezultatul se înmulţeşte cu 8 şi apoi se împarte la 9 păstrându-se doar ultimele K cifre ale câtului împărţirii. Dacă numărul obţinut are mai puţin de K cifre, atunci acestuia i se adaugă la final cifra 9, până când se completează K cifre.

Pentru a stabili câţi galbeni primeşte al treilea sătean, se aplică aceeaşi regulă, dar pornind de la numărul de galbeni ai celui de-al doilea sătean. Regula se aplică în continuare fiecărui sătean, plecând de la numărul de galbeni primiţi de săteanul care a stat la coadă exact în faţa lui.

Cunoscând numărul de galbeni aleşi de primul sătean, determinaţi numărul de galbeni pe care îl va primi al N-lea sătean.

Având mai multe cuburi la dispoziţie, Crina şi Rareş au hotărât să construiască clădiri prin alipirea a două sau mai multor turnuri. Turnurile au fost obţinute prin aşezarea cuburilor unul peste celălalt. Înălţimea unui turn este dată de numărul de cuburi din care este format.
Clădirile construite au fost aşezate în linie, una lângă alta formând astfel o stradă, pe care cei doi copii se vor plimba.

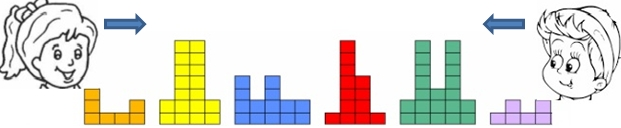
Pentru numerotarea clădirilor Crina şi Rareş au stabilit următoarele reguli:

• Crina porneşte dintr-un capăt al străzii, iar Rareş din celălalt capăt al acesteia; fiecare dintre ei traversează strada complet, trecând prin dreptul fiecărei clădiri
• Crina lipeşte pe fiecare clădire câte un bileţel pe care scrie înălţimea turnurilor din care aceasta este construită, în ordinea în care ea le vede când trece prin dreptul lor (de exemplu, pentru imaginea de mai sus, Crina va lipi pe prima clădire un bileţel pe care va scrie numărul 3112 deoarece, primul turn e format din 3 cuburi, următoarele două turnuri ale acestei clădiri sunt formate din câte un cub iar cel de-al patrulea turn e format din 2 cuburi);
• Rareş va proceda la fel, dar începe plimbarea din celalalt capăt al străzii. În exemplul din imagine, el va lipi pe prima clădire pe care o întâlneşte un bileţel pe care scrie numărul 2121.
• La finalul plimbării, Crina şi Rareş îşi dau seama că există clădiri pe care au lipit amândoi bileţele cu numere identice.

a) Care este înălţimea celui mai înalt turn şi care este numărul clădirilor care au în construcţia lor un astfel de turn?
b) Care este numărul clădirilor pe care cei doi copii au lipit bileţele cu numere identice?
c) Care este cel mai mic număr de cuburi necesar pentru a completa clădirile astfel încât, pe fiecare clădire, bileţelul pe care îl va lipi Crina să conţină acelaşi număr cu cel pe care îl va lipi Rareş? Cuburile din care a fost construită iniţial clădirea nu se pot muta.

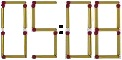Lui Gigel, elev în clasa a V-a, îi place grozav de tare să se joace cu cifrele, cu numerele şi creează tot felul de probleme pe care apoi încearcă să le rezolve. Acum se joacă cu o cutie de chibrituri şi formează cu ele cifre. Apoi privirea i-a căzut pe cadranul unui ceas electronic şi a văzut că cifrele sunt formate din segmente orizontale şi verticale şi a început să formeze cu chibriturile cifrele care indică ora (vezi figura). Şi imediat şi-a pus o întrebare: “oare dacă am n chibrituri puse vertical şi m chibrituri puse orizontal, care este ora minimă pe care o pot forma cu aceste chibrituri?”

Fiind date un număr n de chibrituri verticale şi un număr m de chibrituri orizontale, să se scrie un program care determină numărul de ore posibile, ora minimă şi ora maximă care se pot forma cu aceste chibrituri, în modul indicat mai sus, utilizând toate chibriturile respective şi nemodificând orientarea acestora.

Ana şi Bogdan au găsit la bunicul lor o cutie cu N beţe de aceeaşi lungime. După câteva minute de joacă urmează cearta. Bunicul le-a propus să rupă cele N beţe și apoi Ana să primească fragmentele din mâna stângă, iar Bogdan fragmentele din mâna dreaptă. Zis şi făcut. Copiii au luat fragmentele, le-au numerotat fiecare cu numere de la 1 la N, le-au măsurat şi acum îşi doresc să lipească fragmentele primite, dar mai au nevoie de câteva informaţii.

Cunoscând N numărul de beţe, a1, a2,…, aN lungimile fragmentelor primite de Ana şi b1, b2,…, bN lungimile fragmentelor primite de Bogdan, să se scrie un program care să determine:

a) lungimea iniţială a beţelor;
b) lungimea celui mai lung băţ care se poate obţine prin lipirea unui fragment aparţinând Anei cu un fragment care aparţine lui Bogdan;
c) numărul beţelor de lungime maximă care se pot obţine prin lipirea unui fragment aparţinând Anei cu un fragment care aparţine lui Bogdan.

Avem la dispoziţie patru numere naturale N, A, B, C, precum şi trei cifre c1, c2, c3 distincte două câte două.

Să se determine numărul natural minim, strict mai mare decât N, care are exact A cifre c1, B cifre c2, C cifre c3 şi nu conţine alte cifre.

“Arrows” este un joc care se joacă pe o tablă dreptunghiulară a cărei suprafaţă este împărţită în NxM celule, aranjate pe N linii şi M coloane. În fiecare celulă se află o săgeată (sus, jos, stânga sau dreapta), ca în figura de mai jos:

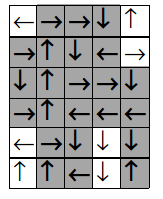
Când este la mutare, un jucător poate alege o poziţie de start pe care plasează un jeton, apoi deplasează jetonul la celula învecinată în sensul indicat de săgeată. Deplasarea continuă până când jetonul părăseşte tabla de joc, caz în care jucătorul obţine un punctaj egal cu numărul de celule parcurse de jetonul său.

Există însă poziţii de start denumite favorabile, pentru care jetonul nu va părăsi niciodată tabla de joc. De exemplu, toate poziţiile din figură cu fundal gri sunt favorabile. Jucătorul care alege o poziţie de start favorabilă obţine un punctaj egal cu numărul de celule distincte vizitate înmulţit cu 1000.

Scrieţi un program care, cunoscând configuraţia tablei de joc, rezolvă una dintre următoarele cerinţe:

1. determină punctajul pe care îl obţine un jucător care plasează jetonul său pe o poziţie de start specificată;
2. determină numărul de celule favorabile de pe tabla de joc;
3. determină punctajul maxim pe care jucătorul îl poate obţine la o mutare, alegând convenabil poziţia de start.

La proba de sărituri cu schiurile din cadrul jocurilor olimpice de iarnă participă N concurenți, numerotați cu numere de la 1 la N.

Regulile de desfășurare a probei sunt următoarele:

• concurenții evoluează pe rând, în ordine de la 1 la N;
• fiecare concurent va efectua o singură săritură;
• după efectuarea săriturii fiecare concurent primește un anumit punctaj;
• pe tot parcursul concursului, comisia de arbitri are obligația să alcătuiască o listă cu punctajele obținute de concurenți, în ordinea evoluției lor;
• evoluția unui concurent durează exact un minut;
• nu se face pauză între evoluțiile a doi concurenți care au numere de ordine consecutive;
• afișarea punctajului nu necesită timp suplimentar după efectuarea săriturii;
• proba se încheie la un minut după evoluția ultimului concurent.

Pe tot parcursul concursului se ține în mod neoficial și un clasament parțial, pe baza rezultatelor obținute de concurenții care au evoluat până în acel moment. Asta pentru că șeful comisiei de arbitri are o curiozitate aparte și pune K întrebări sub forma următoare: Câte minute s-a ocupat primul loc din clasament cu un punctaj egal cu X puncte? Dacă nici un concurent nu s-a clasat pe primul loc cu X puncte atunci primește ca răspuns valoarea 0.

Scrieți un program care determină răspunsul pentru fiecare dintre cele K întrebări puse de șeful comisiei de arbitri.

Se consideră un şir x1, x2,…, xn format din n numere naturale distincte. O secvenţă de număr maxim de elemente vecine în şir, de forma xi, xi+1,…, xk-1, xk, xk+1,…, xj (1≤i<k<j≤n) cu proprietatea că xi < xi+1 < ...< xk-1 < xk > xk+1 > ... > xj, se numeşte munte cu vârful xk. Două secvenţe munte au maxim un element comun în şir. O secvenţă munte are cel puţin 3 elemente. Un exemplu de şir format cu valorile 3 4 6 8 nu conţine nicio secvenţă munte, iar unul format cu valorile 3 4 8 1 2 5 0 conţine 2 secvenţe munte: 3 4 8 1 şi 1 2 5 0.

După determinarea tuturor secvenţelor munte şi a vârfurilor acestora, se elimină din şir vârfurile secvenţelor munte şi procedura continuă repetat cu determinarea noilor secvenţe munte şi a vârfurilor lor din şirul nou obţinut. Procedura se opreşte în momentul în care în şir nu mai există nicio secvenţă munte.

Scrieţi un program care citeşte numerele n, x1, x2, …, xn şi apoi determină:

a) numărul de secvenţe munte din şirul iniţial;
b) numărul total de secvenţe munte obţinute pornind de la şirul iniţial până la cel care nu mai conţine nicio secvenţă munte;
c) numărul de elemente din şirul final care nu mai conţine secvenţe munte.