Lista de probleme 1991

Ada și Ben sunt pasionați de jocurile pe calculator și tocmai au descoperit cea mai recentă versiune a jocului 2048.

Scrieţi un program care să citească numerele naturale N (numărul inițial de piese) și M (numărul maxim de mutări), un șir de N numere reprezentând, în ordine, numerele înscrise pe cele N piese și cel mult M caractere din mulțimea {S, D} ce reprezintă mutările fixate de către Ada și Ben, și care determină:

a) numărul X de mutări efectuate până la încheierea jocului;
b) numărul maxim Y înscris pe una dintre piese la încheierea jocului;
c) numărul maxim Z de fuzionări efectuate la o mutare.

La un concurs de robotică, în timpul prezentării, un roboţel cu corp cilindric cu diametrul de o unitate scapă de sub control şi se deplasează într-un ring de formă dreptunghiulară. Ringul este împărţit în N x M pătrate identice, cu latura de o unitate, aşezate pe N linii şi M coloane.

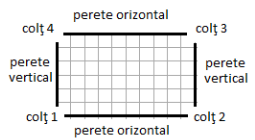Robotul poate părăsi ringul numai pe la colţuri, acestea fiind numerotate de la 1 la 4, colţul cu numărul 1 fiind cel din stânga jos apoi restul fiind numerotate în sens trigonometric. Suprafaţa ringului este delimitată de exterior prin intermediul a patru pereţi despărţitori: doi pereţi “verticali” (aşezaţi de la colţul 1 la colţul 4, respectiv de la colţul 2 la colţul 3) şi doi pereţi “orizontali” (aşezaţi de la colţul 1 la colţul 2, respectiv de la colţul 3 la colţul 4), fără a bloca ieşirile, ca în desenul alăturat.

Se cere să se determine:

a) după câte secunde şi prin ce colţ al ringului va ieşi robotul;
b) de câte ori se ciocneşte robotul de pereţii orizontali şi verticali, rezultând o schimbare de direcţie, până la ieşirea din ring.

Se consideră N vectori cu elemente întregi, numerotați de la 1 la N, sortați crescător, fiecare vector având un număr precizat de elemente.

Să se răspundă la Q întrebări de tipul:
a) 1 i j, cu semnificaţia: care este minimul dintre modulele diferențelor oricăror două elemente, primul element aparținând vectorului numerotat cu i, iar cel de al doilea element aparținând vectorului numerotat cu j ?
b) 2 i j, cu semnificația: care este valoarea ce se găsește pe poziția mediană în vectorul obținut prin interclasarea vectorilor având numerele de ordine i,i+1,…,j (i<j).

Fie un număr natural N. Spunem că (a, b, c) este un triplet geometric limitat de N, dacă a, b și c sunt trei numere naturale astfel încât 1 ≤ a < b < c ≤ N și \( b = \sqrt {a \cdot c} \).

Să se determine numărul tripletelor geometrice limitate de numărul natural N.

Să se determine un șir strict crescător, cu lungimea N, format din numere naturale nenule, \( 1 ≤ a_1 < a_2 < a_3 < … < a_N ≤ [2 \cdot N \cdot \sqrt{N}] \), cu proprietatea că oricare trei termeni distincți ai șirului nu sunt în progresie aritmetică, adică pentru oricare numere naturale i, j şi k cu 1 ≤ i < j < k ≤ N, este îndeplinită condiţia: \( a_i + a_j \neq 2 \cdot a_j \). Prin [x] s-a notat partea întreagă a lui x.

De exemplu, pentru N = 5, cel mai mare termen al șirului va trebui să fie mai mic sau egal cu \( [2 \cdot 5 \cdot \sqrt{5} ] \), adică aN ≤ 22, deci o soluție este: 1, 2, 4, 5, 10.

Un gard este format din mai multe plăci dreptunghiulare. Fiecare placă este, la rândul ei, construită din NxM cărămizi. Una dintre plăci ridică o problemă, deoarece este deteriorată. Placa este reprezentată pe hârtie cu ajutorul unei matrice cu N linii și M coloane, numerotate de la 1 la N, respectiv de la 1 la M. Matricea conține doar valori 0 și 1, și respectă următoarele reguli:

• un element egal cu 1 indică prezența în aceea poziție a unei cărămizi, iar un element egal cu 0 indică absența ei;
• linia 1 și linia N conțin numai valori egale cu 1, pentru că marginea de sus și cea de jos a plăcii este intactă;
• din orice element egal cu 1, situat în interiorul matricei, se poate ajunge pe linia 1 sau pe linia N sau pe amândouă, mergând doar în sus sau doar în jos, parcurgând numai valorile egale cu 1;
• există cel puțin o coloană stabilă (formată numai din elemente egale cu 1).

Se dorește modificarea plăcii și pentru aceasta se pot șterge din matrice maximum K coloane alăturate. După ștergere se alipesc coloanele rămase și se deplasează pe verticală partea de sus a plăcii spre cea de jos, până când se va forma o coloană stabilă.

Să se determine înălțimea minimă Hmin pe care o poate avea placa ștergând cel mult K coloane alăturate. Identificați numărul minim de coloane alăturate care trebuie șterse pentru a obține înălțimea Hmin.

Se consideră un șir de N numere naturale, notate x 1, x 2, x 3,…, x N. Definim pentru orice pereche de indici i, j, 1 ≤ i ≤ j ≤ N, distanța între elementele x i și x j ca fiind egală cu j – i.

Acest șir va fi codificat după următoarele reguli:

• fiecare element din șir este înlocuit cu indicele celui mai apropiat element din șir (cel față de care distanța este minimă) strict mai mare decât el;
• dacă pentru un element din șir există două elemente care respectă regula de mai sus, atunci el va fi înlocuit cu indicele mai mare, adică al elementului strict mai mare decât el, aflat în dreapta lui;
• elementele de valoare maximă din șir vor fi înlocuite cu -1.

Scrieți un program care codifică un șir de N valori, după regulile descrise.

Babilonienii au dezvoltat un sistem pozițional de scriere a numerelor, în care orice număr natural se poate reprezenta utilizând semnele (unu), (zece) şi spaţii.

Valorile k din {2, 3, … , 9} se obțin scriind semnul de k ori (scrierea babiloniană a lui 3 este ).

Numerele 11, 12, … , 59 se obțin ca succesiuni de semne urmate de semne (43 se reprezintă ca
).

Sistemul folosește gruparea unităților câte șaizeci. Astfel, pentru a scrie umărul șaizeci se folosește același semn ca pentru unu, dar valoarea sa este dată de poziția în care se găsește semnul .

Babilonienii nu foloseau cifra 0. Pentru poziţionarea corectă a semnelor se utiliza spațiu (60 se reprezintă ca , 3600 se reprezintă ca etc.).

Se codifică scrierea babiloniană a unui număr utilizând cifra 1 în locul semnului , cifra 2 în locul semnului și cifra 3 în loc de spațiu.

Dându-se un număr natural n și un șir de n cifre din mulțimea {1, 2, 3}, reprezentând codificarea scrierii babiloniene a unui număr natural, să se determine:
a) numărul maxim de cifre 1 aflate pe poziții consecutive în codificarea scrierii babiloniene date;
b) numărul natural din sistemul zecimal corespunzător scrierii babiloniene date.

Se construieşte un şir de numere naturale care respectă restricţiile:

• primul număr din şir este 9;
• numerele se generează în ordine strict crescătoare;
• şirul conţine toate numerele formate doar cu cifrele 7, 8 şi 9 cu proprietatea că numărul cifrelor 9 este mai mare sau egal decât numărul cifrelor 8 şi numărul cifrelor 8 este mai mare sau egal decât numărul cifrelor 7.
  Scrieți un program care să citească numerele naturale N (reprezentând numărul de iepuraşi) şi a1, a2,…, aN (reprezentând, în ordine, numerele inscripţionate pe feţele gri) și care să determine:
  a) Numărul minim de operaţii TAP necesare rearanjării iepuraşilor;
  b) Cel mai mic număr aflat pe o faţă albă care nu se vede, în cazul în care au rămas cartonaşe neîntoarse. Dacă toate cartonaşele au fost întoarse (la toate fiind vizibilă faţa albă) se va afişa cel mai mare număr aflat pe o faţă albă a unui cartonaş.

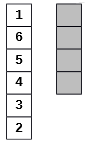
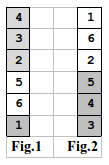Se consideră un joc de cărţi cu un număr nelimitat de coloane. Iniţial, pe prima coloană există, într‑o ordine oarecare, N cărţi cu numere distincte din mulţimea {1,2,…,N}, următoarele coloane fiind vide (fără cărţi). Numim secvenţă de la sfârşitul coloanei ultima sau ultimele două sau ultimele trei etc. cărţi din coloană care au scrise pe ele numere consecutive în ordine crescătoare, considerate de jos în sus. De exemplu, în figurile 1 şi 2 sunt reprezentate două astfel de coloane cu câte 6 cărţi având numere între 1 şi 6. În figura 1, secvenţa de la sfârşitul coloanei este formată doar din cartea 1. În figura 2, secvenţa de la sfârşitul coloanei este formată din cărţile 3, 4 şi 5. Se observă că în coloana din figura 1 mai există o secvenţă formată din cărţile 2, 3 şi 4, dar aceasta nu este la sfârşitul coloanei.

Operaţiile permise ale jocului sunt:

A. mutarea secvenţei de cărţi de la sfârşitul unei coloane pe o coloană nouă, dacă acea coloană este vidă (nu conţine nicio carte);
B. mutarea secvenţei de cărţi de la sfârşitul unei coloane la sfârşitul altei coloane cu cărţi, doar dacă secvenţa mutată formează o secvenţă de numere consecutive cu cele de pe cartea sau cărţile aflate la sfârşitul coloanei respective.

Se doreşte ca, printr-un număr minim de operaţii permise, să se obţină pe una dintre coloane toate numerele de la 1 la N, în ordine crescătoare, considerate de jos în sus.

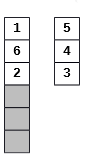
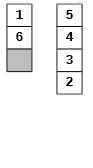
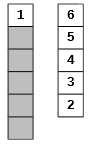
De exemplu, de la configuraţia iniţială din figura 2 se va obţine, printr-o operaţie A, configuraţia 1 de mai jos. Apoi, printr-o operaţie B, se obţine configuraţia 2, printr-o nouă operaţie B se obţine configuraţia 3, apoi se mută secvenţa 2,3,4,5,6 pe o coloană vidă (operaţia A), apoi se mută secvenţa 1 peste secvenţa 2,3,4,5,6 (operaţia B) şi se obţine, pe coloana a doua, configuraţia finală cerută.

Configurația 1	Configurația 2	Configurația 3	Configurația 4	Configurația 5

Cerința

Cunoscând valoarea lui N, precum şi valorile cărţilor de pe prima coloană, să se determine numărul minim de operaţii prin care se poate obţine secvenţa 1, 2, …, N pe una dintre coloane.