Lista de probleme 17
Filtrare
#3775
prosum
Se dau N numere naturale a[1], a[2], ..., a[N] şi un număr natural nenul M. Să se determine numărul perechilor de indici (i, j), cu i < j, cu proprietatea că numărul a[i]*a[j]+a[i]+a[j] este divizibil cu M.
Lot informatică 2021
- Fișiere
- Mihai Bunget
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Căutare binară
- Cmmdc
- Invers modular
- Cautare binara
- set
- Map
#4487
moser
Se consideră un cerc. Pe cerc se desemnează N puncte oarecare. Dacă tragem linii între toate perechile de puncte, care este numărul maxim de bucăți în care poate fi descompus cercul? Să se răspundă la Q astfel de scenarii.
#3819
Anagrame5
Se dau două șiruri de caractere s și t, să se calculeze câte subșiruri din s sunt anagrame ale șirului t.
infoleague.net propunere runda 1, problema 2
- Consola
- Cozma Tiberiu Ștefan
- concurs
- Clasa 10 Probleme diverse Combinatorică
- Invers modular
#3589
probleme
O culegere conține n probleme, dintre care m sunt probleme ușoare. În câte moduri pot fi alese k probleme, astfel încât între cele k probleme alese să existe cel puțin s probleme ușoare?
- Fișiere
- Sándor Lukács
- medie
- Clasa 10 Probleme diverse Combinatorică
- Combinatorica
- Invers modular
- Exponentiere rapida
#3853
Clasa0
Astăzi în clasa 0 profesoara a numit Q copii și le-a dat 3 numere, a, b și c, copiii trebuiau să spună care este rezultatul calculului \({a}^{{C}_{b}^{c}}\), adică \({a}^{ \frac{b! }{{c! *(b-c)! }}}\), modulo \(10^9+7\). Copiii nu au știut să răspundă la întrebări așa că voi trebuie acuma să le spuneți rezultatul.
CsAcademy
#1110
Spion1
Spionul 008 vrea să găsească o locație secretă în junglă, având asupra lui un dispozitiv de localizare. Iniţial spionul se află la intrarea în junglă pe nivelul 1 şi cu fiecare pas, el avansează de la nivelul i la nivelul i+1, ajungând la locaţia secretă, aflată pe ultimul nivel, în poziţia u faţă de marginea stângă a nivelului curent. Pentru a ajunge în locaţia secretă, el poate să se deplaseze cu o poziţie spre Sud-Est (codificat cu caracterul E) sau spre Sud-Vest (codificat cu caracterul V), trecând de pe nivelul i pe nivelul i+1 cu viteză constantă. Numărul de poziţii de pe un nivel creşte cu unu faţă de nivelul anterior, conform imaginii alăturate. Numim traseu o succesiune formată din caracterele E sau V, corespunzătoare deplasării spionului de pe nivelul 1 la locaţia secretă. Pentru exemplul din figura alăturată succesiunea de caractere VEEVE reprezintă un traseu ce corespunde locaţiei secrete din poziţia 4 a nivelului 6.
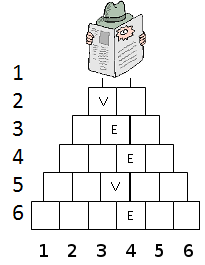
Cunoscând succesiunea de caractere corespunzătoare unui traseu, determinaţi:
a) poziţia locației secrete de pe ultimul nivel;
b) numărul de trasee distincte pe care le poate urma spionul plecând din poziţia inițială pentru a ajunge în locaţia secretă corespunzătoare traseului dat. Două trasee se consideră distincte dacă diferă prin cel puţin o poziţie.
ONI 2014, Clasa a X-a
- Fișiere
- Vlad Laurentiu Nicu
- concurs
- Clasa 10 Probleme diverse Combinatorică
- Triunghiul lui Pascal
- Exponentiere rapida
- Invers modular
#2000
Sir9
Corneluș a învățat să numere. El pornește întotdeauna de la 1, numără din 1 în 1, nu greșește niciodată numărul următor, însă ezită uneori și atunci spune numărul curent de mai multe ori. Sora lui, Corina, îl urmărește și face tot felul de calcule asupra modurilor în care numără fratele ei. Astfel, ea urmărește până la cât numără (U), câte numere spune în total (N) și, pentru a aprecia cât de ezitant este, numărul maxim de repetări (R) ale unei valori.
1) Cunoscând numărul total de numere N și ultimul număr spus U, trebuie să calculați câte șiruri diferite au exact N numere și se termină cu numărul U.
2) Cunoscând numărul total de numere N și numărul maxim de repetări R ale unei valori, trebuie să calculați câte șiruri diferite au exact N numere și fiecare valoare se repetă de cel mult R ori.
Deoarece numărul de șiruri poate fi foarte mare, calculați restul împărțirii acestui număr la 20173333.
OJI 2017, Clasa a X-a
- Fișiere
- Rodica Pintea
- concurs
- Clasa 10 Probleme diverse Combinatorică
- Combinari
- Invers modular
#3691
crescator2
Fie un șir a de N numere întregi. Trebuie construit un nou șir b (tot cu N elemente) astfel:
- dacă \( {a}_{i}>0 \), atunci \( {b}_{i}={a}_{i} \)
- dacă \( {a}_{i}=0 \), atunci \( {b}_{i} \) poate avea orice valoare strict pozitivă
- dacă \( {a}_{i}<0 \), atunci \( {b}_{i} \) poate avea orice valoare strict pozitivă cu excepția lui \( -{a}_{i} \)
Se garantează că \( {a}_{1} \) și \( {a}_{N} \)au valori strict pozitive și între oricare două valori strict pozitive se va afla cel mult una strict negativă.
Știindu-se șirul a, să se calculeze numărul de moduri de a forma șirul b astfel încât acesta să fie crescător (nu neapărat strict). Deoarece acest număr poate fi foarte mare, se va afișa doar restul împărțirii la 1.000.000 007.
Concursul Național Info Pro, Etapa II
- Fișiere
- Alexandra Udriștoiu
- concurs
- Clasa 10 Probleme diverse Combinatorică
- Combinari
- Invers modular
- Programare dinamică
- Stars and Bars
#3703
Potter
În Hogwarts există o tablă de șah cu N linii și M coloane. Harry Potter a găsit plasate, de către Hagrid, T ture care apără fiecare linia și coloana pe care este așezată. El trebuie să plaseze în siguranță K pioni pe tablă, adică fără ca vreunul dintre ei să fie atacat de vreo tură. Tabla de șah din Hogwarts este specială deoarece în cadrul unei celule pot fi plasați chiar și mai mulți pioni simultan! Cunoscând toate aceste reguli, ajutați-l pe Harry Potter să determine în câte modalități poate plasa în siguranță toți cei K pioni pe tabla de șah.
Concursul Național Info Pro, Etapa IV
- Fișiere
- Dana Lica, Florian Ușurelu
- concurs
- Clasa 10 Probleme diverse Combinatorică
- Exponentiere rapida
- Invers modular
- Combinatorica
- Stars and Bars
#3834
B-FlippedCards2
După ce Le. Quack a avut mare succes cu noul lui joc de cărți a decis să se apuce de scamatorii, pentru ca este pasionat de cărți îi cere patronului N cărți. Acesta așează toate cărțile pe față și se pregătește să facă o scamatorie. Acesta vrea să întoarcă toate cărțile pe spate, o operație constă în alegerea a mai multor cărți pe față adiacente și întoarcerea lor. Ca să facă totul mai interesant el alege Q persoane din public si acestea îi spun două numere, X Y, cu semnficația ca Le. Quack să facă toate trucurile posibile cu X cărți inițial pe față toate și exact Y operații de întoarcere astfel încât să ajungă cu toate cele X cărți alese pe spate. După fiecare dintre cele Q persoane el repune toate cărțile pe față. Le. Quack trebuie să numere toate posibilitățile de a face fiecare truc de magie doar că nu este bun la informatică așa că vă cere ajutorul!
infoleague.net runda antrenament 2, problema B.
- Fișiere
- Tudor Iacob
- concurs
- Clasa 10 Probleme diverse Combinatorică
- Stars and Bars
- Combinari
- Permutari
- Invers modular
- Aritmetica modulara
- Precalculare