Lista de probleme 54
Filtrare
#2233
Patrate2
Ovi este un băieţel foarte isteţ căruia îi place să scrie pe asfalt cu creta şi să ţopăie. El desenează cu cretă roşie un dreptunghi de lăţime exact 2 metri şi lungime N metri, pe care îl împarte în pătrate egale de latură 1 metru, unele laturi interioare fiind desenate cu cretă roşie, iar restul laturilor interioare cu cretă albă. Ovi porneşte din pătratul aflat în colţul stânga sus al dreptunghiului, sărind dintr-un pătrat în altul vecin pe linie sau coloană, cu condiţia ca latura care desparte cele două pătrate să nu fie colorată în roşu. El îşi doreşte ca prin sărituri succesive să ajungă în toate pătratele dreptunghiului, dar a observat că numai pentru anumite variante de colorare a laturilor pătratelor reuşeşte acest lucru.
Ajutaţi-l pe Ovi să numere câte posibilităţi de colorare în roşu a unor laturi interioare ale pătratelor sunt astfel încât plecând din colţul stânga sus să poată ajunge prin sărituri în oricare alt pătrat.
ONI 2004
- Fișiere
- Dan Pracsiu
- concurs
- Clasa 11 Probleme diverse Probleme diverse
- Numere mari
#1760
Optim
Gigel primea de la mama lui, ca temă, o foaie pe care era scris un şir de N numere întregi. Singurul calcul pe care ştia să îl facă până acum era suma tuturor numerelor. Pentru aceasta el plasa N-1 semne de adunare, +, între numerele aflate pe poziţii consecutive în şir şi calcula astfel suma acestor numere. Între timp a crescut şi a învăţat şi operaţia de înmulţire pentru care foloseşte semnul *. Din şirul celor N-1 semne de adunare, îi trece prin minte să înlocuiască K semne + cu K semne *.
Îşi dă seama că tema se complică, deoarece înmulţirile trebuie efectuate înaintea adunărilor, dar nu se dă bătut şi duce calculul până la capăt.
Scrieţi un program care să determine valoarea minimă pe care o poate obţine şi valoarea maximă pe care o poate obţine după înlocuirea menţionată.
ONI 2012, Clasa a VIII-a
- Fișiere
- Daniela Lica
- concurs
- Clasa 11 Probleme diverse Probleme diverse
#3698
bemo
Se dă o matrice cu R linii şi C coloane de numere distincte de la 1 la R * C. Bemo, personajul emoţional, doreşte să urmărească cel mai bun drum din colţul superior stânga, de coordonate (1, 1), în colţul inferior dreapta, de coordonate (R, C). Un drum este o secvenţă de numere din matrice în care fiecare număr se găseşte în jos sau la dreapta numărului anterior, adică dacă (i, j) este poziţia unui număr de pe un drum, atunci următorul număr poate fi cel de pe poziţia (i + 1, j) sau cel de pe poziţia (i, j + 1). Pentru a determina dacă un drum A este mai bun decât un drum B, numerele fiecărui drum se vor sorta şi se va alege cel mai mic lexicografic.
ONI 2013, Clasele XI-XII
- Fișiere
- Marius Stroe
- concurs
- Clasa 11 Probleme diverse Probleme diverse
#694
sam
Aranjăm primele N numere naturale nenule sub forma unui șir A[1], A[2], ..., A[N].
Fie X[1], X[2],...,X[K] (K ≥ 3), un subșir al șirului A. Numim extrem local al subșirului X termenul din mijlocul unei secvențe de lungime trei din subșir, X[i-1], X[i], X[i+1], cu proprietatea: X[i-1]<X[i]>X[i+1], 1<i<K sau X[i-1]>X[i]<X[i+1], 1<i<K.
Vom nota cu nrex(X) numărul de extreme locale ale subșirului X.
Spunem că un subșir X[1], X[2],...,X[K] (K≥2) al șirului A este subșir alternant dacă nrex(X)=K-2, adică exceptând primul și ultimul termen din subșir toți ceilalți termeni sunt extreme locale ale subșirului X.
Dintre toate subșirurile alternante ale șirului A ne interesează cele de lungime maximă pe care le vom numi subșiruri alternante maximale.
Cunoscând N și tabloul A se cere să se determine restul obținut la împărțirea dintre numărul M al subșirurilor alternante maximale ale tabloului A și numărul 1000003.
Lot Juniori, Sovata, 2014
- Fișiere
- concurs
- Clasa 11 Probleme diverse Probleme diverse
#1115
Avarcolaci
Un vârcolac bântuie ulițele satului Bosston, semănând panică printre săteni. Satul Bosston este compus din 2*N săteni, fiecare dintre aceștia fiind rudă cu exact un vârcolac. Vârcolacii sunt codificați cu numere naturale. Pentru a afla care este vârcolacul care le cauzează probleme, aceștia s-au dus la vraciul local. Acesta a spus că, dacă există un vârcolac V astfel încât oricum s-ar împărți cei 2*N săteni în două grupuri de N săteni, există cel puțin un sătean în primul grup și cel puțin un sătean în al doilea care să fie rude cu V, atunci vârcolacul V sigur este cel care bântuie satul. Dacă nu există un astfel de vârcolac, atunci sătenii nu își pot da seama cine le bântuie satul.
Cunoscând N și indicii vârcolacilor cu care se înrudesc fiecare dintre cei 2*N săteni, să se determine vârcolacul care bântuie satul, în cazul în care acesta există.
ONI 2014, Clasele XI-XII
- Fișiere
- Andrei Parvu
- concurs
- Clasa 11 Probleme diverse Probleme diverse
- Element majoritar
#1117
Volum
K.L. 2.0 și-a dorit o piscină pe un grid A cu N linii și M coloane. Cum K.L. 2.0 nu a fost foarte inspirat, el a uitat să își niveleze terenul înainte de a construi piscina, astfel încât fiecare celulă de coordonate (i, j) a gridului are o înalțime Ai,j (1 ≤ i ≤ N și 1 ≤ j ≤ M). La un moment dat începe o ploaie puternică, care umple piscina cu apă. După terminarea ploii, K.L. 2.0 se întreabă câtă apă are în piscină.
Dintr-o celulă apa se varsă în celulele vecine cu care are o latură comună şi care au înălţimea strict mai mică decât celula curentă. Apa de pe marginea piscinei se scurge în exterior.
Pentru N, M și gridul A date, să se determine volumul de apă care a rămas în piscină.
ONI 2014, Clasele XI-XII
- Fișiere
- Radu Voroneanu
- concurs
- Clasa 11 Probleme diverse Probleme diverse
- Heapuri
- Păduri de mulțimi disjuncte
- Priority queue
#1119
Permutare1
Se dă o matrice cu m linii şi n coloane, fiecare linie reprezentând o permutare. Se ştie că liniile de la 2 la m sunt permutări circulare ale primei linii. Unei linii x (1 ≤ x ≤ m) i se pot aplica următoarele operaţii:
- o permutare circulară la stânga: elementul de pe poziţia
i(1 < i ≤ n) se mută pe poziţiai-1, mai puţin primul primul element, care devine ultimul; - o permutare circulară la dreapta: elementul de pe pozitia
i(1 ≤ i < n) se mută pe poziţiai+1, mai puţin ultimul element care devine primul.
Scopul este să permutăm circular liniile, la stânga sau la dreapta, astfel încât în final toate liniile să fie egale, folosind un număr minim de operaţii.
Dându-se o matrice cu proprietatea din enunţ se cere să se determine numărul minim de operaţii necesare pentru a ajunge la o matrice în care toate liniile sunt egale.
ONI 2014, Clasele XI-XII
- Fișiere
- Andrei Ciocan
- concurs
- Clasa 11 Probleme diverse Probleme diverse
#1203
KSecv
Fie un vector V cu N elemente și un număr K. Vectorul V trebuie împărțit în exact K subsecvențe nevide, astfel încât fiecare element din vector să aparțină exact unei subsecvențe. Această împărțire trebuie făcută astfel încât maximul șmecheriei fiecărei subsecvențe să fie cât mai mic. (Această problemă concepe greșit sistemul de șmecherie și valoare). Șmecheria fiecărei subsecvențe se definește ca fiind parte întreagă din ((Vmax – Vmin + 1) / 2), unde Vmax este valoarea maximă din subsecvență, iar Vmin este valoarea minimă.
Vectorul V de N elemente va fi generat în felul următor: se dă un număr M și 2 vectori A și B de lungime M (indexați de la 0 la M - 1). Fiecare element i, 0 ≤ i < N, din vectorul V va fi calculat cu următoarea formulă: V[i] = (A[i % M] ^ B[i / M]), unde x % y reprezintă restul lui x la împărțirea cu y, x / y reprezintă câtul împărțirii lui x la y și x ^ y reprezintă rezultatul operației xor (sau exclusiv pe biți) dintre x și y.
ONI 2015, Clasele XI-XII
- Fișiere
- Eugenie Daniel Posdarascu, Mihai Ciucu, Radu Voroneanu
- concurs
- Clasa 11 Probleme diverse Probleme diverse
#1204
Trenuri
Gara de Nord este cea mai vestită gară din lume. Japonezii, invidioşi pe sistemul performant de întârziere al trenurilor din Gara de Nord, s-au hotărât să analizeze motivul realizării unei astfel de performanțe.
În Gara de Nord (considerată stația 0) există N trenuri. Pentru fiecare tren i știm că va pleca din Gara noastră protagonistă (stația 0) și o să meargă până la stația statie[i]. Staţiile x şi x+1 sunt legate în mod direct pentru orice x, astfel că trenul i va opri în toate stațiile din intervalul [0, statie[i]]. De asemenea, știm că trenul i are o capacitate egală cu numărul maxim de oameni pe care îl poate transporta. Această capacitate este notată cu capacitate[i].
Avem M pasageri dornici sa folosească magnificul traseu. Pentru fiecare pasager i știm intervalul de stații [a[i], b[i]] pe care vrea să îl parcurgă. Mai exact, acesta vrea să se urce într-un tren în stația a[i] și să coboare în stația b[i].
Din cauza capacității limitate a trenurilor, este posibil ca nu toți pasagerii sa poată obțină un loc și să ajungă în destinația dorită. Să se determine numărul maxim de pasageri care pot ajunge din stația de plecare în stația de sosire, precum și o configurație în care aceștia se pot urca în trenuri.
ONI 2015, Clasele XI-XII
- Fișiere
- Eugenie Daniel Posdarascu
- concurs
- Clasa 11 Probleme diverse Probleme diverse
#1036
Parc1
Un parc de formă dreptunghiulară este format din zone pietonale şi piste de biciclete. Reprezentând harta parcului într-un sistem cartezian, cu coordonata colţului stânga-jos (0,0), pistele de biciclete sunt reprezentate prin dungi orizontale sau verticale colorate cu gri, iar zonele pietonale au culoarea albă, ca în figura din dreapta.
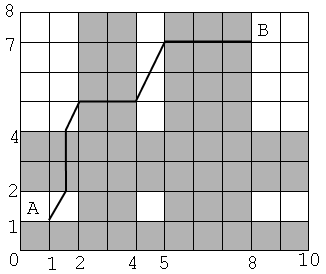 Vizitatorii parcului se pot plimba liber pe zonele pietonale în orice direcţie, însă pistele de biciclete se vor traversa, în linie dreaptă, paralel cu axele. În figura alăturată avem un parc de dimensiuni
Vizitatorii parcului se pot plimba liber pe zonele pietonale în orice direcţie, însă pistele de biciclete se vor traversa, în linie dreaptă, paralel cu axele. În figura alăturată avem un parc de dimensiuni 10 x 8, cu piste de biciclete verticale între 2 şi 4 respectiv 5 şi 8, şi orizontale între 0 şi 1 respectiv între 2 şi 4. Gigel se află în punctul A(1,1) şi poate sa ajungă pe drumul cel mai scurt la prietenul lui, în punctul B(8,7) deplasându-se astfel: porneşte din punctul (1,1) şi parcurge un traseu format din segmente cu extremităţile în punctele de coordonate (1.5 , 2) (1.5, 4) (2 , 5) (4 , 5) (5 , 7) şi în final ajunge în punctul de coordonate (8 , 7).
Lungimea totală a drumului va fi aproximativ 11.4721359.
Cunoscând dimensiunile parcului, coordonatele lui Gigel, coordonatele prietenului lui şi poziţiile pistelor de biciclete, să se calculeze lungimea drumului minim şi numărul drumurilor distincte de lungime minimă.
OJI 2012, clasele XI, XII
- Fișiere
- Zoltan Szabo
- concurs
- Clasa 11 Probleme diverse Probleme diverse