Lista de probleme 45
Filtrare
#3213
NumarDeSubmultimi
Pentru un număr natural nenul n, să se determine numărul de submulțimi ale mulțimii {1, 2,..., n} cu proprietatea că oricare două elemente dintr-o submulțime au diferența în modul strict mai mare decât 1.
Folclorul informatic
- Consola
- Dan Pracsiu
- medie
- Clasa 11 Programare dinamică Probleme de numărare
#4287
Veverita4
În parcul orașului există 4 rânduri de câte n copaci perfect aliniați. Rândurile sunt notate A, B, C și D, iar copacii de pe fiecare rând sunt numerotați de la 1 la n, ca în imaginea de mai jos:

O veveriță jucăușă sare prin copaci astfel:
- pornește dintr-un copac numerotat cu
1; - la fiecare pas sare dintr-un copac numerotat cu
iîntr-un copac numerotat cui+1. Dacă se află într-un copac de pe rândul A, va sări în copacul de pe rândul B, dacă se află într-un copac de pe rândul D, va sări în copacul de pe rândul C, dacă se află în copacul de pe rândul B, va sări în copacul de pe rândul A sau în copacul de pe rândul C, iar dacă se află în copacul de pe rândul C, va sări în copacul de pe rândul B sau în copacul de pe rândul D; - se oprește într-unul dintre copacii numerotați cu
n.
Aflați numărul M de modalități în care se poate deplasa veverița, respectând regulile de mai sus.
#4288
Veverita5
În parcul orașului există 5 rânduri de câte n copaci perfect aliniați. Rândurile sunt notate A, B, C, D și E, iar copacii de pe fiecare rând sunt numerotați de la 1 la n, ca în imaginea de mai jos:
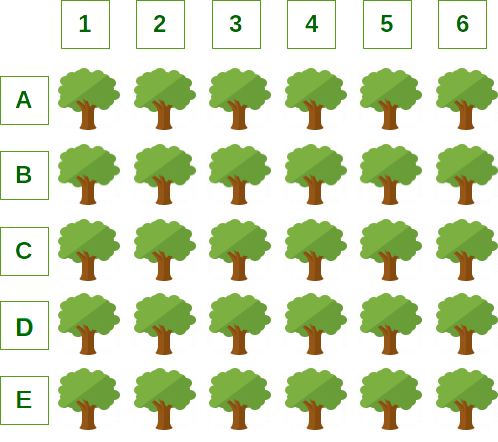
O veveriță jucăușă sare prin copaci astfel:
- pornește dintr-un copac numerotat cu
1; - la fiecare pas sare dintr-un copac numerotat cu
iîntr-un copac numerotat cui+1. Dacă se află într-un copac de pe rândul A, va sări în copacul de pe rândul B, dacă se află într-un copac de pe rândul E, va sări în copacul de pe rândul D, dacă se află în copacul de pe rândul B, va sări în copacul de pe rândul A sau în copacul de pe rândul C, dacă se află în copacul de pe rândul C, va sări în copacul de pe rândul B sau în copacul de pe rândul D,iar dacă se află în copacul de pe rândul D, va sări în copacul de pe rândul C sau în copacul de pe rândul E; - se oprește într-unul dintre copacii numerotați cu
n.
Aflați numărul M de modalități în care se poate deplasa veverița, respectând regulile de mai sus.
- Fișiere
- medie
- Clasa 11 Programare dinamică Probleme de numărare
#4289
VeveritaK
În parcul orașului există k rânduri de câte n copaci perfect aliniați. Rândurile sunt notate A, B, C … K, iar copacii de pe fiecare rând sunt numerotați de la 1 la n, ca în imaginea de mai jos:
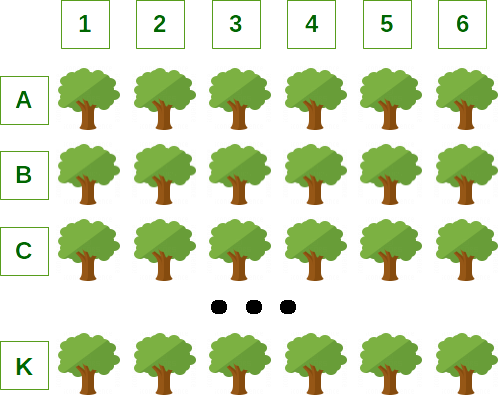
O veveriță jucăușă sare prin copaci astfel:
- pornește dintr-un copac numerotat cu
1; - la fiecare pas sare dintr-un copac numerotat cu
iîntr-un copac numerotat cui+1. Dacă se află într-un copac de pe rândul A, va sări în copacul de pe rândul B, dacă se află într-un copac de pe rândul K, va sări în copacul de pe rândul K-1. Dacă se află în copacul de pe unul dintre rândurile B, C, D, …K-1 va sări în copacul de pe rândul anterior sau în copacul de pe rândul următor. De exemplu, dacă se află în copacul de pe rândul D, va sări în copacul de pe rândul C sau în copacul de pe rândul E; - se oprește într-unul dintre copacii numerotați cu
n.
Aflați numărul M de modalități în care se poate deplasa veverița, respectând regulile de mai sus.
#4569
Veverita_XI
În parcul orașului există k rânduri de câte n copaci perfect aliniați. Rândurile sunt notate A, B, C … K, iar copacii de pe fiecare rând sunt numerotați de la 1 la n, ca în imaginea de mai jos:

O veveriță jucăușă sare prin copaci astfel:
- pornește dintr-un copac numerotat cu
1; - la fiecare pas sare dintr-un copac numerotat cu
iîntr-un copac numerotat cui+1. Dacă se află într-un copac de pe rândul A, va sări în copacul de pe rândul B, dacă se află într-un copac de pe rândul K, va sări în copacul de pe rândul K-1. Dacă se află în copacul de pe unul dintre rândurile B, C, D, …K-1 va sări în copacul de pe rândul anterior sau în copacul de pe rândul următor. De exemplu, dacă se află în copacul de pe rândul D, va sări în copacul de pe rândul C sau în copacul de pe rândul E; - se oprește într-unul dintre copacii numerotați cu
n.
Aflați numărul M de modalități în care se poate deplasa veverița, respectând regulile de mai sus.
- Fișiere
- ușoară
- Clasa 11 Programare dinamică Probleme de numărare
#2882
No_pals
Gioni este un elev foarte pasionat de informatică și îndrăgește în special problemele care se rezolvă cu tehnica programării dinamice. El are un număr natural n și vrea să știe pentru fiecare numar i de la 1 la n câte numere cu i cifre nu sunt palindromuri. Fiindcă acest număr poate să fie foarte mare, se cere afișarea lui modulo 666013.
- Fișiere
- Bogdan Gonda
- ușoară
- Clasa 11 Programare dinamică Probleme de numărare
#2259
dinamica01
Se consideră un număr natural nenul N. Vom considera mulțimea A(N) a numerelor de N cifre nenule care au proprietatea că orice două cifre alăturate sunt de parități diferite. De exemplu 1472 este un număr din mulțimea A(4), dar 1567 nu este pentru că are cifrele alăturate 1 și 5 de aceeași paritate. Să se determine numărul de elemente ale mulțimii A(N). Pentru că acest număr poate fi foarte mare, se va determina modulo 30103.
-
- Consola
- Dan Pracsiu
- ușoară
- Clasa 11 Programare dinamică Probleme de numărare
#4512
dinamica11
Se dă un număr natural nenul n. Se construiește mulțimea numerelor formate din n cifre care au proprietatea că nu au două cifre alăturate care să fie prime. De exemplu 1476 este un număr corect format, dar 1537 nu este pentru că are cifrele alăturate 5 și 3 sau 3 și 7 cu proprietatea că sunt prime.
Să se determine câte numere formate din n cifre au proprietatea că nu au două cifre alăturate care să fie prime. Pentru că acest număr poate fi foarte mare, se va determina modulo 666013.
-
- Consola
- ușoară
- Clasa 11 Programare dinamică Probleme de numărare
#2260
dinamica02
Se consideră un număr natural nenul N. Să se determine numărul de cuvinte de lungime N formate doar din litere mici și cu proprietatea că nu pot exista trei litere alăturate identice. Pentru că acest număr poate fi foarte mare, se va determina modulo 777013.
-
- Consola
- Dan Pracsiu
- ușoară
- Clasa 11 Programare dinamică Probleme de numărare
#2848
dinamica03
Spunem că un cuvânt este valid dacă el este format doar cu litere din mulțimea {a,b,c,d} și literele a și b nu sunt alăturate. De exemplu, cuvintele aaaa, acdca sunt valide, dar abbc și baabd nu sunt. Să se determine numărul cuvintelor valide de lungime n. Pentru că acest număr este foarte mare, se va afișa rezultatul modulo 777013.
Folclorul informatic
- Consola
- Dan Pracsiu
- ușoară
- Clasa 11 Programare dinamică Probleme de numărare