Lista de probleme 63

Se citește un număr natural n cu cel mult 16 cifre. Fie q numărul de cifre ale numărului n. Prin eliminarea unei singure cifre din scrierea numărului n se obține un șir de q numere. Să se afișeze în ordine crescătoare, numerele nenule din acest șir care sunt prime cu numărul n.

Se consideră n intervale de numere întregi [Ai, Bi], 1≤i≤n. Să se determine numărul maxim de intervale care se suprapun (au cel puțin o valoare comună).

Se dau n intervale, să se afișeze care dintre ele includ alte intervale și care sunt incluse într-un interval. Intervalul [a,b] este inclus în intervalul [c,d] dacă c <= a și b <= d (a < b, c < d).

La ora de educație fizică participă n elevi, numerotați de la 1 la n, băieți și fete, pentru fiecare dintre ei cunoscându-se înălțimea, exprimată în centimetri. Profesorul le cere să se alinieze, mai întâi băieții, în ordine descrescătoare a înălțimii, apoi fetele, de asemenea în ordine descrescătoare.

Afișați numerele de ordine ale elevilor în ordinea dorită de profesor. Dacă doi băieți (sau fete) au aceeași înălțime, se va afișa mai întâi elevul cu numărul de ordine mai mic.

La un concurs participă n concurenți, numerotați de la 1 la n. Pentru jurizare s-a format o echipă din m arbitri, fiecare acordând fiecărui concurent un anumit punctaj. Pentru fiecare concurent se calculează media punctajelor, după eliminarea celui mai mare și celui mai mic punctaj acordat.

Afișați clasamentul concursului în ordinea descrescătoare a mediilor calculate. La medii egale se va afișa mai întâi concurentul cu numărul de ordine mai mic.

Fie un şir a[1], a[2], …, a[n] de numere naturale, unde n este impar. Avem la dispoziţie o singură operaţie admisă şi anume: putem aduna la două poziţii diferite din şir o aceeaşi valoare naturală nenulă.

Cerințe:

1. Să se verifice dacă șirul poate să aibă toate elementele egale după aplicarea unei singure operații.
2. Folosind de mai multe ori operaţia admisă, să se obţină șirul cu toate elementele egale, dar valoarea egală obţinută să nu depăşească dublul valorii maxime din şirul iniţial.

Primăria orașului ONI a făcut un contract cu firma Gigel.SRL în vederea amenajării gardului Grădinii Botanice. Șeful firmei a constatat că gardul cu pricina este format doar din trei tipuri de scânduri care sunt aranjate fără nicio regulă. Fiind un tip cu “gust estetic” și-a propus să rearanjeze scândurile astfel încât gardul să conțină scândurile grupate astfel: primele să fie scândurile de primă dimensiune (cea mai mică) apoi cele mijlocii, iar ultimele să fie cele de dimensiunea cea mai mare. Echipa care a fost desemnată să execute lucrarea are un singur muncitor care dorește să știe care este numărul minim de schimbări pe care ar trebui să le facă astfel încât să rezolve problema și scândurile să fie ordonate așa precum a decis șeful firmei. Operația de schimbare constă în alegerea a două scânduri diferite și așezarea uneia în locul celeilalte.
Dându-se un număr n ce reprezintă numărul de scânduri care alcătuiesc gardul, precum şi modul în care sunt aranjate scândurile în gard, să se determine care este numărul minim de schimbări ce trebuie realizat astfel încât gardul să aibă scândurile aranjate crescător. Scândurile sunt codificate în funcție de dimensiune prin valorile 1, 2 și 3.

Se consideră o matrice A cu următoarele proprietăţi:

• conţine n linii şi m coloane;
• conţine doar valorile 0 şi 1;
• pe fiecare linie valorile sunt plasate în ordine crescătoare.

Definim o submatrice determinată de perechea de linii L1 şi L2 (L1 ≤ L2) şi de perechea de coloane C1 şi C2 (C1 ≤ C2) ca fiind totalitatea elementelor matricei A[i,j] pentru care L1 ≤ i ≤ L2 şi C1 ≤ j ≤ C2.
Dacă toate elementele unei submatrice sunt egale cu 0, atunci submatricea se numeşte nulă.
Asupra matricei A putem efectua una sau mai multe operaţii de interschimbări de linii. Prin astfel de interschimbări liniile matricei pot fi rearanjate astfel încât matricea A să conţină cel puţin o submatrice nulă cu număr maxim de elemente.
Fiind dată o astfel de matrice se cere să se determine numărul maxim de zerouri dintr-o submatrice nulă ce se poate obţine printr-o rearanjare a liniilor matricei date.

A fost odată ca niciodată un împărat puternic care avea o grădină minunată, situată pe un teren de formă dreptunghiulară din jurul palatului. În grădină creştea un măr cu mere de aur, dar împăratul nu a putut să se bucure vreodată de merele din pom deoarece grădina a fost mereu atacată de tâlhari şi merele au fost furate. Cu toate că aceasta a fost păzită zi şi noapte de cei mai viteji ostaşi din împărăţie, ei nu au putut face faţă tâlhăriilor. Deznădăjduit, împăratul şi-a pus în gând să taie pomul cu mere de aur, dar fiul său cel mic, Prâslea, l-a rugat să-l lase şi pe el să-şi încerce norocul. Prâslea a cugetat foarte bine la cele întâmplate şi a procedat astfel:

• a delimitat în grădină, de-a lungul acesteia, N parcele alăturate, numerotate de la stânga la dreapta cu valori în ordine, de la 1 la N. Dintre acestea, a dat spre pază fraţilor şi verişorilor săi M parcele, iar restul de N-M parcele oştenilor din împărăţie. Cele N-M parcele date oştenilor sunt identice şi au fiecare lăţimea L.
• a măsurat distanţa D la care se află pomul cu merele de aur faţă de marginea din stânga a grădinii, pentru a întări chiar el paza parcelei în care e situat acesta.

Cerinţă

a) Cunoscând lăţimea fiecărei parcele, determinaţi cel mai mare număr de parcele alăturate, de lăţime L fiecare, date spre pază oştenilor ;
b) Determinaţi numărul de ordine al parcelei în care se află pomul cu merele de aur.

Jocul pe care îl joaca Robo atunci când se plictisește este un joc inteligent pentru roboței. Pe ecranul tabletei lui roboțești, sunt N căsuțe de formă pătrată, cu latura egală cu 1. Căsuțele sunt așezate pe un rând, una lângă alta, fiind etichetate, în această ordine, cu numere de la 1 la N. Fiecare căsuță conține câte un număr natural, identificatorul câte unuia dintre prietenii săi, roboței, ca și el. Identificatorii se pot repeta.

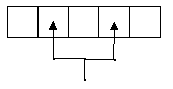Robo poate interschimba conținutul a două căsuțe, numai dacă distanța dintre centrele acestora pe orizontală este egală cu distanța dintre brațele sale; distanța, pe orizontală, dintre centrele a două căsuțe etichetate cu i, respectiv cu j, este j-i (1≤i<j≤N).

El își poate fixa în orice moment distanța dintre brațe la 1 sau își poate dubla distanța curentă dintre brațe, de oricâte ori este necesar, fără a depăși valoarea N-1. Astfel, distanța dintre brațele sale poate fi 1, apoi, prin dublare, 2, apoi, prin dublare 4, apoi, prin dublare 8 etc. La începutul jocului, distanța dintre brațele lui Robo este 1. De fiecare dată când consideră convenabilă distanța dintre brațe, realizează o interschimbare.

Se cere ca Robo să așeze identificatorii în căsuțe în ordine crescătoare, prin maximum 12500 interschimbări de tipul celei precizate mai sus.