Lista de probleme 108

Maria dansează! Lecțiile de dans se desfășoară într-o sală imensă, împărțită în n*m sectoare pătratice cu dimensiunea 1, dispuse pe n linii și m coloane. În anumite sectoare se află diverse obstacole, astfel că acele sectoare nu pot fi utilizate pentru dans. Maria are nevoie pentru dans de o zonă dreptunghiulară de dimensiuni p, q, cu laturile paralele cu pereții sălii, care să nu conțină obstacole și vrea ca în fiecare zi să danseze într-o zonă diferită de cele în care a dansat deja. Determinați numărul de zile în care Maria poate dansa așa cum își dorește.

Aky, un elev pasionat de matematică, analiza într-o zi curios o matrice pătratică de dimensiune N. Acesta a observat că această matrice are anumite submatrice, la rândul lor pătratice, ale căror elemente sunt egale. Astfel și-a pus o întrebare: pentru o matrice dată, care este submatricea pătratică de dimensiune maximă a acesteia cu toate elementele egale pe care o pot obține, știind că am voie să schimb valoarea a maxim K elemente din matricea dată cu orice valoare consider. Acesta ar rezolva problema de unul singur, dar este ocupat chiar acum deci vă cere vouă ajutorul!

“Avioane pe hârtie” este un joc ce se joacă în doi, fiecare jucător având la dispoziţie o foaie de hârtie (de matematică) şi ceva de scris.

Dată fiind configuraţia caroiajului şi poziţiile loviturilor lansate de adversar, să se determine:

a. numărul total de avioane desenate în caroiaj;
b. numărul de avioane de fiecare tip;
c. numărul de avioane avariate, fără a fi doborâte;
d. numărul de avioane doborâte.

Într-o cameră sunt aşezate n*m acvarii identice, pe n rânduri, câte m pe fiecare rând, unul lângă altul. În fiecare acvariu se află un singur peşte. Peştele poate fi de culoare roşie (culoare codificată cu r) sau albastră (codificată cu a). La fiecare moment de timp t=1,2,3,.., peştii îşi modifică simultan culoarea astfel: fiecare peşte se colorează în culoarea pe care au avut-o la momentul t-1 majoritatea peştilor din acvariile învecinate (ca în desenul de mai jos, sunt cel mult 8 acvarii vecine notate cu V1, V2, V3,…, V8). În cazul în care numărul peştilor vecini roşii este egal cu numărul peştilor vecini albaştrii, peştele studiat îşi va păstra culoarea.

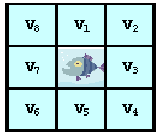
Scrieţi un program care să citească numerele naturale n, m, t şi cele n*m coduri ale culorilor peştilor (cele de la momentul iniţial t=0) şi care să determine şi să afişeze codurile culorilor peştilor de la momentul t.

Se dau două seturi de N, respectiv Q matrice binare (cu valori 0 sau 1), pentru fiecare matrice fiind precizat numărul de linii respectiv de coloane. Să se afișeze numărul aparițiilor matricelor din al doilea set în primul.

Fermierul Quinto are o livadă plină cu pomi fructiferi. Livada are N rânduri, numerotate de la 1 la N, pe fiecare rând aflându-se câte M pomi fructiferi, numerotaţi de la 1 la M. Livada lui Quinto este una specială, aşa că pentru unii pomi se cunoaşte cantitatea de fructe (exprimată în kg) care poate fi culeasă, iar pentru alţii aceasta poate fi determinată pe baza unei formule. Quinto şi-a propus să recolteze C kg de fructe din pomii aflaţi în livada lui. Acesta foloseşte un utilaj modern pentru culesul fructelor. Utilajul poate fi folosit pe oricare din rândurile livezii, dar poate aduna doar fructele dintr-un şir consecutiv de pomi, începând cu primul pom de pe rândul respectiv, neavând posibilitatea de a culege parţial fructele dintr-un pom. Preocupat de frumuseţea livezii sale, Quinto s-a gândit la restricţii suplimentare pentru recoltarea cantităţii C de fructe. Astfel, el doreşte să adune fructele din pomi de pe maximum R rânduri diferite, pentru ca N-R rânduri să rămână complete. De asemenea, el doreşte să culeagă cu prioritate pomii care au o cantitate cât mai mică de fructe, pentru ca în livadă să rămână cei mai roditori pomi. Quinto şi-a dat seama că este dificil să culeagă fix C kg de fructe, prin urmare este mulţumit şi cu o cantitate mai mare, care respectă celelalte condiţii impuse de el.

Determinaţi cea mai mică valoare X posibilă astfel încât să se poată culege, în condițiile de mai sus, o cantitate de cel puțin C kg de fructe și orice pom din care se culeg fructe să conțină cel mult X kg de fructe.

Tudor a primit un joc educaţional numit “Roboţel” cu ajutorul căruia va învăţa punctele cardinale Nord, Est, Sud, Vest. Jocul constă dintr-un roboţel care se deplasează pe o tablă de forma unei matrici pătratice, împărţită în R linii şi R coloane. Fiecare căsuţă, aflată la intersecţia dintre o linie şi o coloană, este fie căsuță „liberă”, fie căsuță „semnalizator”, caz în care este etichetată cu una din literele N, E, S, V, reprezentând 4 sensuri posibile de deplasare. Când roboțelul ajunge într-o „căsuţă semnalizator”, el îşi schimbă sensul de deplasare astfel:

• Dacă căsuţa este etichetată cu N atunci roboţelul se va deplasa în continuare de jos în sus;
• Dacă căsuţa este etichetată cu E atunci roboţelul se va deplasa în continuare de la stânga la dreapta;
• Dacă căsuţa este etichetată cu S atunci roboţelul se va deplasa în continuare de sus în jos;
• Dacă căsuţa este etichetată cu V atunci roboţelul se va deplasa în continuare de la dreapta la stânga.

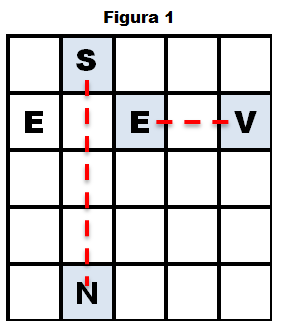Două căsuțe semnalizator formează o pereche „blocantă” dacă:

• Se află pe aceeași linie și conțin literele E și V, căsuța cu E are coloana mai mică decât a celei etichetate cu V și între ele, pe aceeași linie nu există alte căsuțe semnalizatoare.
• Se află pe aceeași coloană și conțin literele S și N, căsuța cu S are linia mai mică decât a celei etichetate cu N și între ele, pe aceeași coloană nu există alte căsuțe semnalizatoare.

În figura 1, de exemplu, sunt 2 perechi blocante: Perechea (1,2) (5.2) și perechea (2,3) (2,5).

Roboţelul porneşte din căsuţa (1,1), aflată pe prima linie și prima coloană şi dacă aceasta este liberă, se deplasează, în cadrul primei linii, de la stânga la dreapta. În cazul în care căsuța de pornire (1,1) este semnalizator, atunci roboțelul se va deplasa pe direcția indicată de litera cu care este etichetată. Considerând că roboțelul se deplasează pe tablă, el se oprește doar în următoarele situații:

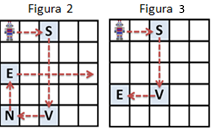• Roboţelul intră într-o căsuţă liberă aflată pe prima sau ultima linie, respectiv prima sau ultima coloană, caz în care dacă s-ar menține sensul deplasării actuale roboțelul ar părăsi tabla;
• Roboțelul intră într-o „căsuţă semnalizator” a unei perechi blocantă și se va opri în cealaltă căsuță a perechii.

De exemplu, în Figura 2, roboțelul ajunge în căsuța liberă (3,5) unde se oprește. În Figura 3, roboțelul se va opri în căsuța (4,1) deoarece dacă ar schimba sensul spre Est, ar reveni în ultima căsuță semnalizator vizitată, (4,3).
Roboțelul înaintează o căsuță într-un pas, în sensul de deplasare.

Scrieţi un program care, cunoscând numărul R de linii şi coloane și cele K căsuţe semnalizator, determină:

1. Toate perechile blocante de pe tablă;
2. Numărul de pași efectuați pe fiecare sens în parte: Nord, Est, Sud și Vest

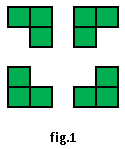Pietrele preţioase au fascinat omenirea încă din timpuri străvechi iar cele mai renumite dintre ele, cristalele, au devenit atât simbolul durităţii cât şi al eternităţii. În urma unui studiu ştiinţific, pe un eşantion de formă dreptunghiulară se pot observa diferite tipuri de molecule, dispuse într-o geometrie perfectă, pe M rânduri a câte N molecule fiecare, aliniate una lângă alta. O formaţiune cristalizabilă este alcătuită din 3 molecule de acelaşi tip, învecinate două câte două, având una dintre cele patru forme din imaginea alăturată (fig.1).

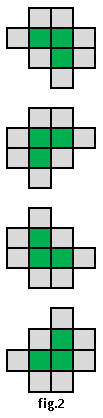Fiecare formaţiune este înconjurată de jur-împrejur, ca în fig.2, de un înveliş special format şi el din molecule identice, de alt tip decât cele din formaţiunea cristalizabilă pe care o înconjoară şi o izolează de restul formaţiunilor moleculare. În acest fel, fiecare moleculă din formaţiunea cristalizabilă se învecinează la Nord, Sud, Est şi Vest cu o moleculă din aceeaşi formaţiune cristalizabilă sau cu o moleculă din învelişul special.

Fiecare formaţiune cristalizabilă se bombardează cu raze X şi în acest fel are loc cristalizarea, proces prin care învelişul special se extinde peste formaţiunea cristalizabilă pe care o înconjoară, formând o singură structură din care se va dezvolta cristalul.

Cerințe

1. Determinaţi numărul formaţiunilor cristalizabile ce pot fi identificate pe eşantionul analizat.
2. Afişaţi eşantionul rezultat după cristalizare.

Considerăm că toate punctele de coordonate întregi din plan sunt colorate în negru, cu excepţia a n puncte care sunt colorate în roşu. Două puncte roşii aflate pe aceeaşi linie orizontală sau pe aceeaşi linie verticală (adică puncte care au aceeaşi ordonată sau aceeaşi abscisă) pot fi unite printr-un segment. Colorăm în roşu toate punctele de coordonate întregi de pe acest segment. Repetăm operaţia cât timp se obţin puncte roşii noi. Cunoscând coordonatele celor n puncte care erau iniţial roşii, aflaţi numărul maxim de puncte roşii care vor exista în final.

Se consideră o matrice dreptunghiulară A cu m linii şi n coloane cu valori 0 sau 1, liniile şi coloanele fiind numerotate de la 1 la m, respectiv de la 1 la n. Numim dreptunghi de colţuri (x1, y1) (x2,y2) cu x1 < x2 şi y1 < y2 mulţimea elementelor A[i][j] cu x1 ≤ i ≤ x2 si y1 ≤ j ≤ y2. Numim perimetru al dreptunghiului de colţuri (x1, y1) (x2, y2) mulţimea elementelor A[i][j] pentru care (i = x1 şi y1 ≤ j ≤ y2) sau (i = x2 şi y1 ≤ j ≤ y2) sau (j = y1 şi x1 ≤ i ≤ x2) sau (j = y2 şi x1 ≤ i ≤ x2).

Determinaţi diferenţa maximă dintre numărul de elemente egale cu 1 şi numărul de elemente egale cu 0 aflate pe perimetrul aceluiaşi dreptunghi, precum şi numărul de dreptunghiuri pentru care se obţine această diferenţă.