Exerciții 1366
Rezultate 1366
Exercițiul #553
Utilizând metoda backtracking se generează în ordine crescătoare numere naturale de câte patru cifre din mulțimea A={1,2,3,4,5}, numere care nu conțin două cifre impare alăturate. Primele opt numere generate sunt, în această ordine, 1212, 1214, 1221, 1222, 1223, 1224, 1225, 1232. Numărul de valori generate care au cifra miilor egală cu 2 şi cifra unităților egală cu 4 este:
| Varianta 1 |
20 |
| Varianta 2 |
16 |
| Varianta 3 |
12 |
| Varianta 4 |
9 |
Exercițiul #557
O matrice de adiacență prin care poate fi reprezentat graful orientat cu 3 vârfuri, reprezentat în figura de mai jos, este:
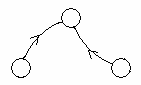
| Varianta 1 |
0 1 0 0 0 1 0 0 0 |
| Varianta 2 |
0 0 1 0 0 1 0 0 0 |
| Varianta 3 |
0 0 0 0 0 1 0 0 1 |
| Varianta 4 |
0 1 0 1 0 1 0 1 0 |
Exercițiul #558
Se consideră arborele cu rădăcină, având 10 noduri, numerotate de la 1 la 10, cu vectorul de „tați” t=(3,3,8,0,8,9,9,4,4,9). Enumerați toate nodurile arborelui care au exact doi fii.
Scrieți nodurile în ordine crescătoare, separate prin exact un spațiu!
Exercițiul #561
Pentru ca graful orientat cu 5 vârfuri, reprezentat în figura alăturată, să devină graf tare conex, numărul minim de arce care trebuie adăugate acestuia este:
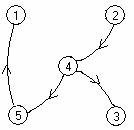
| Varianta 1 |
1 |
| Varianta 2 |
2 |
| Varianta 3 |
3 |
| Varianta 4 |
4 |
Exercițiul #562
Având la dispoziție cinci flori diferite, lalea, narcisă, mac, frezie, garoafă, se utilizează metoda backtracking pentru a obține toate posibilitățile de a forma un aranjament floral, ştiind că se folosesc toate cele cinci flori şi contează ordinea de aşezare a acestora. Primele patru soluții obținute sunt, în această ordine:
(lalea, narcisă, mac, frezie, garoafă)(lalea, narcisă, mac, garoafă, frezie)(lalea, narcisă, frezie, mac, garoafă)(lalea, narcisă, frezie, garoafă, mac)
Care este penultima soluție generată?
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #563
Având la dispoziție cinci flori diferite, lalea, narcisă, mac, frezie, garoafă, se utilizează metoda backtracking pentru a obține toate posibilitățile de a forma un aranjament floral, ştiind că se folosesc toate cele cinci flori şi contează ordinea de aşezare a acestora. Primele patru soluții obținute sunt, în această ordine:
(lalea, narcisă, mac, frezie, garoafă)(lalea, narcisă, mac, garoafă, frezie)(lalea, narcisă, frezie, mac, garoafă)(lalea, narcisă, frezie, garoafă, mac)
Care este ultima soluție generată?
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #565
Se consideră un graf neorientat cu 6 noduri şi 9 muchii. Numărul de muchii ce trebuie adăugate, pentru ca graful obținut să fie complet, este:
| Varianta 1 |
5 |
| Varianta 2 |
6 |
| Varianta 3 |
12 |
| Varianta 4 |
15 |
Exercițiul #567
Se consideră un arbore cu rădăcină având 6 noduri, numerotate de la 1 la 6, şi muchiile [1, 2], [1, 3], [2, 4], [3, 5], [3, 6]. Considerând că rădăcina este nodul numerotat cu 1 şi că ea este situată pe nivelul 0 al arborelui, scrieți toate nodurile situate pe nivelul 2 al arborelui dat.
Scrieți nodurile în ordine crescătoare, separate prin exact un spațiu!
Exercițiul #568
Utilizând metoda backtracking se generează toate numerele pare cu câte trei cifre, cifre care aparțin mulțimii {7, 8, 1, 6, 2, 3}. Primele 4 soluții generate sunt, în această ordine: 778, 776, 772, 788. Cea de a 8-a soluție generată este:
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #639
Se consideră arborele cu 7 noduri, numerotate de la 1 la 7, reprezentat prin vectorul de „taţi” (5,4,5,3,0,3,1). Mulţimea tuturor “frunzelor” arborelui este:
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|