Exerciții 1333
Rezultate 1333
Exercițiul #999
Un arbore cu 19 noduri, numerotate de la 1 la 19, are ca rădăcină nodul numerotat cu 1; nodul 1 are un singur fiu, și anume nodul 2, iar fiecare nod i (i≥2) fie este frunză, fie are drept fii (descendenți direcți) noduri numerotate cu valori din intervalul [i+1,2·i-1]. Numărul maxim de frunze ale arborelui este:
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #1002
Utilizând metoda backtracking, se generează toate băuturile obținute amestecând sucurile a cel puțin două fructe distincte din mulțimea {afine, caise, lămâi, mere, pere}. Primele cinci soluţii obţinute sunt, în această ordine: (afine, caise), (afine, caise, lămâi), (afine, caise, lămâi, mere), (afine, caise, lămâi, mere, pere) și (afine, caise, lămâi, pere). A șasea soluţie este:
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #1004
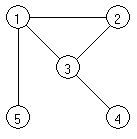
Indicați un lanț elementar în graful neorientat cu 5 noduri, numerotate de la 1 la 5, reprezentat mai jos.
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #1005
Indicați valorile ce pot reprezenta numărul de fii ai fiecăruia dintre cele șase noduri ale unui arbore cu rădăcină.
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #1009
Utilizând metoda backtracking, se generează, în ordine strict descrescătoare, toate numerele naturale de câte patru cifre distincte din mulțimea {0, 1, 2, 3, 4, 5}. Primele șase numere generate sunt, în această ordine: 5432, 5431, 5430, 5423, 5421, 5420. Al șaptelea număr generat este:
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #1010
Un graf neorientat are 20 de noduri și 10 muchii. Numărul maxim de componente conexe pe care le poate avea acest graf este:
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #1019
Care dintre următoarele afirmații este adevărată pentru orice graf neorientat?
A) Numărul vârfurilor cu gradul impar este par.
B) Suma gradelor tuturor vârfurilor este pară.
| Varianta 1 |
Doar A). |
| Varianta 2 |
Doar B). |
| Varianta 3 |
Și A), și B). |
| Varianta 4 |
Nici A), nici B). |
Exercițiul #1020
Care dintre următoarele afirmații este adevărată pentru orice graf neorientat cu mai mult de două vârfuri?
| Varianta 1 |
Nu există două vârfuri cu același grad. |
| Varianta 2 |
Cel puțin două vârfuri au același grad. |
| Varianta 3 |
Cel puțin trei vârfuri au același grad. |
| Varianta 4 |
Toate vârfurile au același grad. |
Exercițiul #1041
Care dintre cele patru variante de mai jos nu poate reprezenta secvența gradelor vârfurilor unui graf neorientat?
| Varianta 1 |
1, 1, 1, 2, 2, 3 |
| Varianta 2 |
1, 1, 3, 3, 3, 5 |
| Varianta 3 |
1, 1, 2, 3, 4, 5 |
| Varianta 4 |
1, 4, 4, 4, 4, 5 |
Exercițiul #1043
Matricea de adiacență a unui graf neorientat cu 1020 de noduri are 200 de elemente nenule. Numărul maxim de componente conexe ale grafului este:
| Varianta 1 |
1002 |
| Varianta 2 |
1005 |
| Varianta 3 |
1006 |
| Varianta 4 |
1010 |