Acest site foloseşte cookies. Navigând în continuare, vă exprimaţi acordul asupra folosirii cookie-urilor.
Soluții trimise
Rezumat problemă
SumMax1
#1623
Avem o matrice triunghiulară cu n linii, cu elemente numere întregi. În această matrice putem construi un traseu după următoarea regulă:
- primul element al traseului este elementul
a1,1 - dacă elementul
ai,japarţine traseului, atunci următorul element al traseului poate fi doarai+1,jsauai+1,j+1, pentru orice1≤j≤i<n. - traseul se va codifica cu numerele de ordine ale coloanelor, parcurgând liniile de la
1lan. Valoarea traseului este egală cu suma elementelor ce îl formează.
Traseul evidenţiat în exemplul din dreapta are valoarea5+4+6+5+4=24, şi se codifică cu1,2,3,3,4.
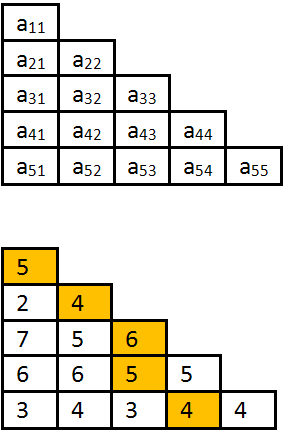
Fie mulţimea tuturor traseelor de valoare maximă generate în ordine lexicografică și numerotate. Pentru exemplul de mai sus avem șase trasee de lungime maximă:
- traseul 1.
1 1 1 1 2 (5+2+7+6+4=24) - traseul 2.
1 1 1 2 2 (5+2+7+6+4=24) - traseul 3.
1 2 2 2 2 (5+4+5+6+4=24) - traseul 4.
1 2 3 3 4 (5+4+6+5+4=24) - traseul 5.
1 2 3 4 4 (5+4+6+5+4=24) - traseul 6.
1 2 3 4 5 (5+4+6+5+4=24)
Cunoscând dimensiunea și elementele unei matrice triunghiulare, respectiv două numere naturale st şi dr (st≤dr), se cere să se determine:
- Numărul total al traseelor de valoare maximă. În cazul în care această valoare depășește
2000000000, se va tipări valoarea2000000001; - Traseele cu numerele de ordine
st,st+1, … ,dr.
OJI 2016, Clasele XI-XII
| ID | Utilizator | Problema | Data încărcării | Stare | ||
|---|---|---|---|---|---|---|
| SumMax1 | 14 Martie 2025, 01:24 | Evaluare finalizată | 20 | |||
| SumMax1 | 14 Martie 2025, 01:22 | Evaluare finalizată | 15 | |||
| SumMax1 | 14 Martie 2025, 01:22 | Evaluare finalizată | 0 | |||
| SumMax1 | 14 Martie 2025, 01:19 | Evaluare finalizată | 15 | |||
| SumMax1 | 14 Martie 2025, 01:03 | Evaluare finalizată | 15 | |||
| SumMax1 | 14 Martie 2025, 01:02 | Evaluare finalizată | E.C | |||
| SumMax1 | 14 Martie 2025, 01:02 | Evaluare finalizată | E.C | |||
| SumMax1 | 14 Martie 2025, 01:01 | Evaluare finalizată | 15 | |||
| SumMax1 | 14 Martie 2025, 01:01 | Evaluare finalizată | 15 | |||
| SumMax1 | 14 Martie 2025, 01:00 | Evaluare finalizată | 15 | |||
| SumMax1 | 14 Martie 2025, 00:40 | Evaluare finalizată | 0 | |||
| SumMax1 | 14 Martie 2025, 00:39 | Evaluare finalizată | 5 | |||
| SumMax1 | 14 Martie 2025, 00:38 | Evaluare finalizată | 5 | |||
| SumMax1 | 14 Martie 2025, 00:37 | Evaluare finalizată | 5 | |||
| SumMax1 | 14 Martie 2025, 00:36 | Evaluare finalizată | 0 | |||