Soluții trimise
Rezumat problemă
Cerc1
#708
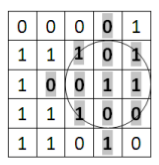 Considerăm un caroiaj dreptunghiular cu
Considerăm un caroiaj dreptunghiular cu L linii şi C coloane. Liniile sunt numerotate de la 1 la L de sus în jos şi coloanele de la 1 la C, de la stânga la dreapta. Caroiajul este împărţit în L*C pătrate cu latura egală cu două unităţi (2). În fiecare pătrat al caroiajului se găseşte una dintre valorile 0 sau 1. Se cunoaşte o poziţie (i, j) a unuia dintre pătratele caroiajului (1 ≤ i ≤ L, 1 ≤ j ≤ C).
Trebuie construit un cerc care să îndeplinească următoarele proprietăţi:
- Centrul cercului să coincidă cu centrul pătratului din poziţia
(i, j); - Raza cercului să fie un număr natural nenul;
- Diferenţa dintre numărul de valori
1şi numărul de valori0aflate în pătratele acoperite de cerc să fie maximă.
Considerăm că un pătrat este acoperit de cerc dacă pătratul şi cercul au cel puţin un punct comun (aflat pe contur sau în interior). Dacă un pătrat este complet inclus în interiorul cercului se consideră că şi acel pătrat este acoperit de cerc (în figură, cercul desenat “acoperă” inclusiv pătratul din poziţia (3, 4) ). Cercul din figură are raza 3.
Determinaţi diferenţa maximă ce se poate obţine cu constrângerile de mai sus.
Lot Juniori, Botosani, 2012
| ID | Utilizator | Problema | Data încărcării | Stare | ||
|---|---|---|---|---|---|---|
| Cerc1 | 10 Octombrie 2022, 18:55 | Evaluare finalizată | 100 | |||