Lista de probleme 38
Filtrare
#1921
Ceas
Săturat de ținut uși, Hodor s-a hotărât să devină ceasornicar. Maestrul ceasornicar îi spune lui Hodor că îl va învăța, doar dacă va trece un test. Maestrul îi da lui Hodor un sistem de coordonate xOy, și un ceas cu raza r, al cărui centru se află în centrul sistemului de coordonate O(0,0). Ceasul contine doar limba care indica orele, de lungime r. Inițial limba indică ora 12:00, cu vârful în punctul de coordonate A(0,r). Hodor trebuie să afle coordonatele vârfului limbii, după h ore și m minute.
- Fișiere
- Vlad Tiberiu Mihailescu
- medie
- Clasa 10 Probleme diverse Geometrie
#2006
Mana
Înștiințat de atacul orcilor, Gandalf și-a luat măsurile de precauție. Credinciosul spion i-a adus acestuia o hartă care arată pozițiile celor n orci. Harta poate fi reprezentată ca un sistem cartezian de coordonate. Gandalf vrea să folosească o vrajă astfel încât să anihileze cel puțin k orci. De asemenea, acesta vrea să folosească cât mai puțină mana. Știind că, dacă utilizează r mana (r număr natural), și vraja este folosită în punctul de coordonate (x,y), acesta anihilează toți orcii din interiorul cercului cu centrul în (x,y) de rază r, aflați mana minimă necesară pentru a anihila k orci.
- Fișiere
- Vlad Tiberiu Mihailescu
- dificilă
- Clasa 10 Probleme diverse Geometrie
#2846
Petale
Fiind dat un cerc de rază r, care este raza R a n cercuri astfel încât acestea să atingă într-un singur punct cercul inițial și intersecția dintre oricare două astfel de cercuri să fie tot de un singur punct?
Best of CNCV /w '18 - '19
- Consola
- Valentin Vintilă
- dificilă
- Clasa 10 Probleme diverse Geometrie
- CNCV
#1609
paralele
Se dau N drepte paralele în sistemul de axe ortogonale xOy, acestea intersectând axa Ox în N puncte de abscise întregi x1, x2, ... , xN. Determinaţi numărul maxim M de perechi de drepte dintre cele date, pentru care distanţa dintre dreptele din orice pereche este aceeaşi.
- Fișiere
- Mihai Bunget
- ușoară
- Clasa 10 Probleme diverse Geometrie
#1628
Patrate1
Pe o foaie cu pătrăţele se stabileşte un sistem de coordonate în care o intersecţie primeşte coordonatele (0,0), astfel încât fiecare intersecţie a caroiajului are coordonate numere întregi. Pe acest caroiaj se desenează un pavaj cu dreptunghiuri, în care fiecare dreptunghi are o lăţime L şi o înălţime H date, iar punctul de coordonate (0,0) este un colţ de dreptunghiuri. În acest mod, fiecare intersecţie a pavajului are coordonate de forma (L*i,H*j), cu i şi j întregi.
Se mai dă o pereche de întregi x şi y şi se consideră segmentul de dreaptă ce uneşte punctul de coordonate (0,0) cu punctul de coordonate (x,y).
Se cere să se determine câte dreptunghiuri ale pavajului sunt intersectate de segmentul considerat. Un dreptunghi se consideră intersectat de segment dacă are cel puţin un punct interior comun. Cu alte cuvinte, dacă segmentul doar atinge colţul unui dreptunghi, nu se consideră că îl intersectează.
Concursul Interjudetean „MARIAN ŢARINĂ” 2015
- Fișiere
- Lupşa Radu
- concurs
- Clasa 10 Probleme diverse Geometrie
#2538
xOy
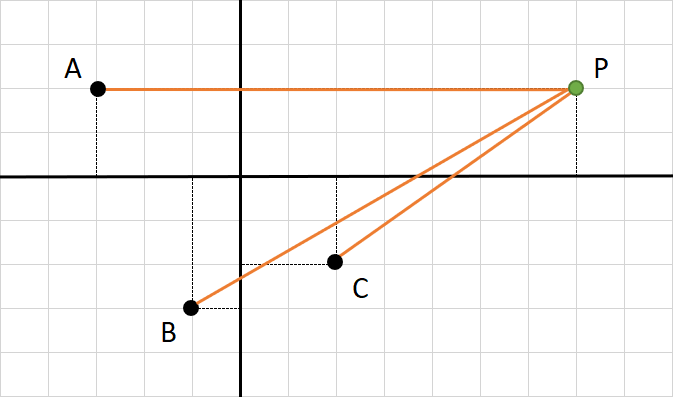
Laur desenează un sistem cartezian xOy și marchează 3 puncte necoliniare pe care le notează cu A, B și C, având coordonatele cunoscute \( (X_A, Y_A) \), \( (X_B, Y_B) \) și \( (X_C, Y_C) \). Vine Laurențiu și îi șterge sistemul de coordonate, lăsând doar punctele A, B și C, iar apoi desenează un alt punct, P, de coordonate nedeterminate. Laur va măsura distanța dintre punctul P și punctele A, B, respectiv C, obținând valori care, ridicate la pătrat, vor fi notate cu \( D_{PA}^{2} \), \( D_{PB}^{2} \), respectiv \( D_{PC}^{2} \). Cunoscându-se coordonatele celor 3 puncte desenate de Laur, precum și pătratul distanțelor dintre punctul P și acestea, să se afle coordonatele în xOy ale punctului P.
Best of CNCV /s '19
- Consola
- Valentin Vintilă
- dificilă
- Clasa 10 Probleme diverse Geometrie
- CNCV
#2060
episodul2
După ce a luat aur la ONI2017, Roby băiatul de aur a decis să ajute la construcția tării Zoomba. Zoli astfel i-a cerut să se ocupe de construirea unui acoperiș ce va acoperi toată țara. Acesta va fi alcătuit din grinzi ce se vor sprijini pe puncte în sistemul cartezian. O grindă va uni două puncte. Acoperișul trebuie construit în așa fel încât, privit de sus, orice unghi format de către două grinzi consecutive să fie ≥ 180 (în cazul în care plouă, nu se dorește ca acesta să țina apa) și să acopere toate punctele de sprijin. Din când în când, Zoli este interesat de aria poligonului format din totalitatea punctelor ce se află sub acoperiș și deasupra axei OX. Astfel se disting următoarele evenimente:
1 x y: Se adaugă punctul de coordonate întregi (x, y) în plan. De acum încolo, se vor putea așeza grinzi pe acesta.
2: Zoli întreabă care este aria poligonului descris mai sus.
- Fișiere
- Bogdan Ioan Popa
- dificilă
- Clasa 10 Probleme diverse Geometrie
#927
DistantaPuncte
Se dau coordonatele în plan a două puncte. Să se afișeze pătratul distanței dintre ele.
- Fișiere
- Marius Nicoli
- ușoară
- Clasa 10 Probleme diverse Geometrie
#928
AriaTriunghi
Se dau coordonatele în plan a trei puncte. Să se afișeze valoarea ariei triunghiului pe care îl formează.
- Fișiere
- Marius Nicoli
- ușoară
- Clasa 10 Probleme diverse Geometrie
#929
PunctSegment
Se dau un punct și un segment în plan. Să se verifice dacă punctul se găsește pe segment.
- Fișiere
- Marius Nicoli
- ușoară
- Clasa 10 Probleme diverse Geometrie