Lista de probleme 38

Se dau două segmente în plan, specificate prin coordonatele capetelor. Să se verifice dacă au cel puțin un punct comun.

Se dau puncte distincte în plan. Asociem fiecărui punct semidreapta care pornește din originea sistemului de coordonate și trece prin acel punct. Să se afișeze punctele în ordine crescătoare a unghiului pe care semidreapta asociată îl face cu semidreapta spre plus infinit a axei OX. Dacă două unghiuri sunt egale se va afișa punctul cel mai apropiat de origine.

Se dau coordonatele în plan pentru n puncte. Să se afișeze valoarea ariei poligonului pe care acestea îl formează.

Dintre n puncte date prin coordonatele lor, să se determine numărul maxim de puncte coliniare.

Se dau în plan, un punct și o dreaptă. Să se determine distanța de la punct la dreaptă.

Se dau în plan, un punct și un segment. Să se determine distanța minimă de la punctul dat la un punct aparținând segmentului.

Se dau coordonatele în plan pentru n puncte care determină un poligon. Se mai dau coordonatele altor m puncte. Să se verifice, pentru fiecare dintre cele m puncte, dacă se găsește sau nu în interiorul (sau pe marginea) poligonului.

Se dau puncte distincte în plan. Să se determine un poligon de arie maximă care are vârfuri dintre punctele date.

În antrenamentul său intens pentru prinderea lui Daffy Duck, celebrul vânător Elmer Fudd a început să vâneze rațe în orașul său preferat, Craiova. Se știe că există N rațe reprezentate prin puncte în planul de coordonate xOy, având coordonatele (x,y) și M ziduri sub forma unor segmente verticale având un capăt pe axa Ox și o anumită înălţime fiecare.

Vânătorul Elmer dorește să împuște cât mai multe rațe. El poate fi poziționat în orice punct de abscisă număr natural nenul, pe axa Ox. O rață poate fi ochită de vânător dacă zidul nu blochează glonțul vânătorului, adică segmentul imaginar delimitat de rață și de vânător nu se intersectează cu nici un zid.

Să se afle numărul maxim de rațe care pot fi ochite de vânătorul Elmer.

Ben are un teren pe care se află o pădure cu arbori seculari. Acolo vrea să-şi construiască o cabană, însă el fiind ecologist nu vrea să taie niciun arbore, ci vrea să găsească cea mai mare suprafaţă dreptunghiulară fără arbori. El caută o suprafaţă dreptunghiulară străjuită doar în colţuri de arbori şi cu laturile paralele cu axele de coordonate. Ben cunoaşte coordonatele tuturor arborilor din pădure şi vă roagă să-l ajutaţi să găsească aria dreptunghiului cu suprafaţă maximă care are arbori doar în cele patru colțuri.

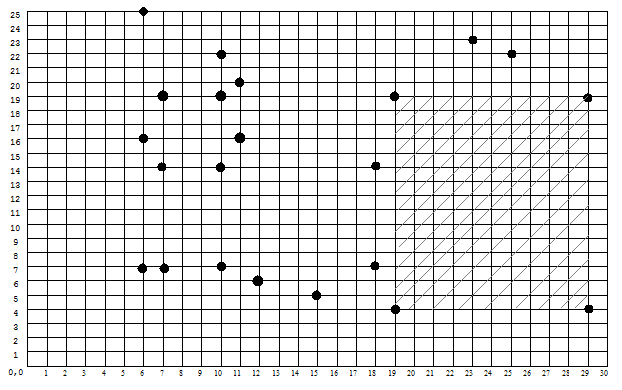
Cunoscând numărul arborilor din pădure şi coordonatele acestora, se cere să se determine aria dreptunghiului de suprafaţă maximă cu copaci doar în cele 4 colţuri, unde Ben intenţionează să-şi construiască cabana.