Soluții trimise
Rezumat problemă
Stiva1
#1114
Olivius d’Info a primit de ziua lui o stivă şi s-a bucurat foarte tare. S-a tot gândit ce să facă cu ea şi a inventat un joc de logică pentru colegii lui de clasă.
În prima fază el a scris mai multe bileţele, conţinând fiecare câte o permutare a primelor n numere naturale nenule: 1, 2, 3, … , n. Bileţelele scrise conţin permutări pentru diferite valori ale lui n.
A clasificat aceste permutări în permutări stivuite şi permutări nestivuite.
O permutare este stivuită dacă se poate obţine pe parcursul introducerii în stivă a numerelor 1, 2, 3, ...,n în această ordine, prin extragerea elementelor, în ordinea indicată în permutare.
O permutare nestivuită este o permutare care NU se poate obţine prin procedeul de mai sus.
Respectând procedeul lui Olivius, pentru n=4, permutarea stivuită (2,1,3,4) se obţine astfel:
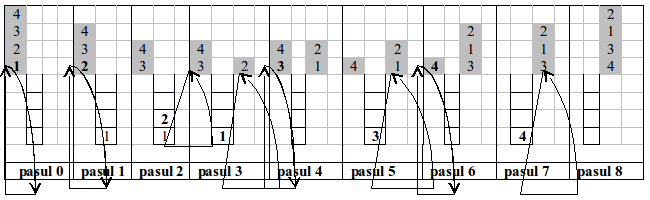
Succesiunile (3,1,2,4) şi (4,2,1,3) sunt permutări nestivuite.
În faza a doua, unele bileţele au fost scurtate din stânga şi/sau din dreapta. Astfel, din permutarea stivuită (2,1,3,4) se pot obţine succesiuni de lungime mai mică: (1,3,4), (2,1,3), (1,3), (3) etc.
Orice succesiune care aparţine unei permutări stivuite, poate aparţine şi unei permutări nestivuite. De exemplu, succesiunea (2,1,3) aparţine atât permutării stivuite (2,1,3,4), cât şi permutării nestivuite (4,2,1,3).
Dându-se mai multe succesiuni de numere naturale distincte, determinaţi, pentru fiecare dintre acestea, dacă aparţin cel puţin unei permutări stivuite.
ONI 2014, Clasa a X-a
| ID | Utilizator | Problema | Data încărcării | Stare | ||
|---|---|---|---|---|---|---|
| Stiva1 | 10 Octombrie 2022, 20:10 | Evaluare finalizată | 100 | |||