În 1736, matematicianul elvețian Leonard Euler a rezolvat o problemă cunoscută astăzi ca “Problema celor șapte poduri din Königsberg”. Prin orașul Königsberg, azi Kaliningrad trece un râu pe care sunt două insule, acestea și malurile fiind unite prin poduri ca în imaginea de mai jos.
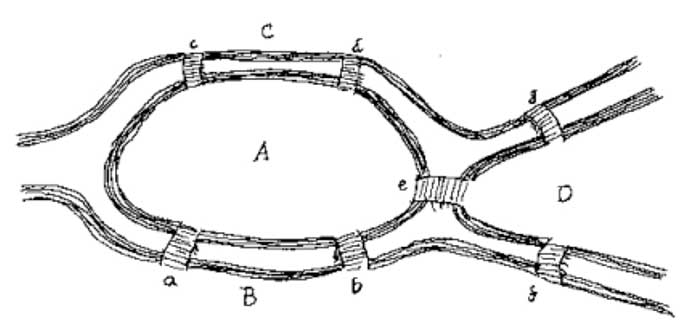
Leonard Euler a demonstrat că nu este posibil ca o persoană să traverseze fiecare pod o singură dată. În onoarea sa, o categorie specială de grafuri se numesc grafuri euleriene.
Definiții:
- Într-un graf neorientat, se numește lanț eulerian un lanț simplu în care apare fiecare muchie (fiind lanț simplu, fiecare muchie apare o singură dată).
- Într-un graf neorientat, se numește ciclu eulerian un ciclu în care apare fiecare muchie.
- Un graf neorientat se numește graf eulerian dacă conține un ciclu eulerian.
Exemplu:
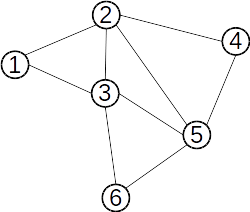
În graful de mai sus ciclul (1 2 4 5 3 6 5 2 3 1) este eulerian.
Teoremă:
Un graf neorientat fără vârfuri izolate este eulerian dacă și numai dacă este conex și toate vârfurile au grad par.
Un graf neorientat fără vârfuri izolate conține un lanț eulerian, dacă și numai dacă este conex și toate vârfurile au grad par, mai puțin două. Aceste vârfuri vor fi extremitățile lanțului eulerian.
Pentru determinarea unui ciclu eulerian se pot folosi mai mulți algoritmi. Unul dintre aceștia este asemănător cu parcurgerea în adâncime. Vom folosi o stivă (eventual memoria STACK prin intermediul recursivității):
- adăugăm pe stivă un vârf oarecare – de exemplu
1; - cât timp stiva nu este vidă
- fie
k– nodul din vârful stivei - determinăm nodurile
xadiacente cuk. Eliminăm muchia[k,x]și adăugăm nodulxpe stivă (apel recursiv)- continuăm cu nodul situat în vârful stivei
- adăugăm nodul
kîntr-o listă - eliminăm nodul
kdin stivă
- fie
- lista construită reprezintă ciclu eulerian
Important:
- la vizitarea unui vârf, acesta nu va fi marcat, pentru a permite revenirea în el;
- finitudinea algoritmului este asigurată de faptul că muchiile se elimină din graf;
Secvență C++:
Considerăm un graf cu n vârfuri, memorat prin intermediul matricei de adiacență, A[][]. Tabloul L[] reprezintă lista în care se memorează ciclul eulerian. Toate variabilele sunt globale:
void Euler(int k)
{
for(int i = 1 ; i <= n ; i ++)
if(A[k][i] == 1)
{
A[k][i] = A[i][k] = 0;
Euler(i);
}
L[++p] = k;
}
...
Euler(1);
...
Algoritmul de mai sus poate fi utilizat și pentru determinarea unui lanț eulerian. Parcurgerea trebuie să înceapă însă din unul dintre vârfurile cu grad impar.
Probleme ataşate
| Nr. | Problema | Clasa | Dificultate | Operații I/O |
|---|---|---|---|---|
| 1 | #0545 - Euler | 11 | medie | fișiere |
| 2 | #1021 - Cartite | 11 | concurs | fișiere |