Lista de probleme 1991

Să ne imaginăm faptul că la un anumit liceu există doar două clase per generație: una de Real și una de Uman. În prezent au loc înscrierile pentru clasa a IX-a. Cele două clase au fiecare câte M locuri disponibile, atât la Real, cât și la Uman. Dacă lista de elevi înscriși la o anumită clasă conține mai mult de M elevi, vor fi admiși acei M elevi care au notele cele mai mari. Ambele clase au deja M elevi înscriși, iar pentru fiecare se știe nota cu care a fost înscris la clasa respectivă.

Mai există însă N elevi, singurii încă neînscriși, care sunt privilegiați în acest proces (fiindcă au terminat gimnaziul la acest liceu). Privilegiul lor constă în următorul fapt: ei se pot înscrie acum, după ce înscrierile publice au fost încheiate, și se cunosc notele de înscriere la ambele clase. Fiecare din cei N elevi are câte două note: nota cu care ar fi înscris la Real și nota cu care ar fi înscris la Uman (acestea pot fi diferite, deoarece examenele de admitere de la cele două clase diferă). Fiecare din cei N elevi va alege să se înscrie în maxim o clasă. Ei își vor coordona alegerile astfel încât să maximizeze numărul de elevi admiși. Deoarece calculele devin destul de complicate, aceștia s-ar putea folosi de ajutorul vostru. Ei doresc răspunsul la două întrebări.

(1) Care este numărul maxim de elevi privilegiaţi care pot fi admiși dacă se pune restricția suplimentară ca toți elevii privilegiați admiși să fie admiși la aceeași clasă?
(2) Care este numărul maxim de elevi privilegiaţi care pot fi admiși dacă aceștia se pot înscrie la clase diferite?

Cu toții știm că popcornul este o adevărată delicatesă culinară. În pregătirile tale pentru lotul de anul acesta (și pentru petrecerile de după), ai făcut comandă de N tipuri de floricele de porumb pentru microunde. Fiecare tip are asociate 3 valori:

• A[i] = Timpul (în secunde) la care orice floricică de acel tip “pocnește”;
• B[i] = Timpul (în secunde) la care orice floricică de acel tip “se arde”;
• C[i] = Cantitatea (în floricele) a respectivului tip.

Mai ai la dispoziție M pungi pentru floricele de unică folosință de capacitate foarte mare (practic, infinită) și un cuptor cu microunde. Cum, bineînțeles, nimănui nu îi plac floricelele nefăcute sau cele arse, îți dorești să le partiționezi convenabil în cele M pungi și apoi să le introduci pe rând în cuptorul cu microunde, setându-i un timp de preparare prep[i] corespunzător, astfel încât după cele M tranșe să obții cât mai multe floricele comestibile.

Formal, o floricică de tipul i introdusă în punga j , setată la timpul (în secunde) de preparare prep[j] este comestibilă dacă și numai dacă A[i] ≤ prep[j] < B[i].

Fiind date cele N tipuri de floricele și numărul de pungi disponibile, trebuie să găsești o partiție convenabilă și timpii optimi de preparare pentru fiecare pungă, astfel încât la final să obții numărul maxim de floricele comestibile, pe care să îl afișezi în fișierul de ieșire. Prea ușor!

Pe o zonă în formă de dreptunghi cu laturile de lungimi N și M se găsesc NxM pătrate de latură 1. În centrul fiecărui pătrat se găsește înfipt câte un ac de grosime neglijabilă. Fiecare ac este descris de înălțimea sa. Această zonă se poate reprezenta ca un tablou bidimensional de dimensiuni N și M, iar fiecare element din matrice reprezintă înălțimea (număr natural nenul) fiecărui ac. În centrul pătratului (N,M) există o cameră de luat vederi de ultimă generație, mobilă, care se poate roti cu 360⁰ în orice plan, situată la nivelul solului. Dimensiunile camerei sunt neglijabile.

Pentru direcția N, camera va vedea acul de coordonatele (3,4) – în totalitate, iar acul (2,4) se va vedea doar parțial . Acul (1,4) nu se vede pentru că este acoperit total de (2,4). În direcția V, camera va vedea doar acul (4,3), deoarece (4,2) și (4,1) sunt acoperite total de (4,3). Pentru celelalte direcții se vor vedea parțial sau în totalitate acele (3,3), (3,2), (3,1), (2,3), (1,3), (2,2), (2,1), (1,2). Acul (1,1) nu se vede din cauza acului (2,2), care îl acoperă total. Acul (2,2) se vede doar parțial, pentru că o parte din el este acoperit de acul (3,3).

1. Câte ace vede camera de luat vederi dacă se poate roti în plan vertical, doar în direcțiile N și V?
2. Câte ace vede camera de luat vederi dacă se poate roti în orice plan și în orice direcții?

Acum iarna s-a terminat și, apropiindu-se sezonul de vară, gospodarii din orașul de pe malul fluviului doresc să pregătească faleza pentru a primi cum se cuvine turiștii. Faleza este sub formă dreptunghiulară cu lungimea de n metri și lățimea de 2 metri. În toamnă ea era pavată cu 2*n dale pătrate cu latura de un metru, lipite una de alta și care acopereau complet zona falezei. În urma iernii grele, unele dale s-au deteriorat și acum se dorește înlocuirea lor.Cum de multe ori oamenii fac treaba doar “pe jumătate”, gospodarii au hotărât să cheltuie cât mai puțin pentru reamenajarea falezei, așa că au decis că nu trebuie neapărat să înlocuiască toate dalele deteriorate, ci doar un număr minim dintre acestea astfel încât să fie posibil să se parcurgă faleza de la un capăt la altul pășind doar pe dale bune (nedeteriorate). De pe o dală pe alta se poate păși doar dacă ele au o latură comună.

Scrieţi un program care să determine numărul minim de dale deteriorate ce trebuie înlocuite astfel încât faleza să
poată fi parcursă de la un capăt la altul.

În timpul activităților din “Săptămâna Altfel” elevii clasei a VII-a doresc să ajute la organizarea cărților din biblioteca școlii. Fiecare carte este etichetată cu un cod care este exprimat printr-un un șir de caractere distincte. Acestea pot fi cifrele 0, 1,..,9 și primele zece litere mici ale alfabetului englez a, b,..,j. Codul identifică în mod unic fiecare carte, adică nu vor exista două cărți cu același cod, dar şi genul literar din care acestea face parte. Cărțile din acelaşi gen literar au codul de identificare format din aceleaşi caractere, distincte, dispuse în altă ordine.

Numim coduri pereche două coduri de identificare care au același număr de caractere și care diferă printr-un
caracter. De exemplu, codurile 42a8 și 2c8a sunt coduri pereche. Pe de altă parte, codurile 42a8 și 248a,
respectiv 42ab și 248c, nu sunt coduri pereche.

Fiind dat șirul celor N coduri de identificare, scrieţi un program care să rezolve următoarele cerinţe:

1. determină numărul de cărți din cel mai numeros gen literar și numărul de genuri literare care au acest număr maxim de cărți.
2. determină numărul de coduri, din șirul celor N, care sunt coduri pereche cu ultimul cod din șir

Scrat și Scratte sunt două veverițe devoratoare de ghinde. Ele trăiesc într-un stejar înalt și culeg ghinde din cele N ramuri ale acestuia. Veverițele vor organiza un concurs: cine culege cele mai multe ghinde în K ture. Într-o tură,
fiecare veveriță se va deplasa de la vizuină până la o ramură a stejarului, de unde va culege cât mai multe ghinde, dar
nu mai mult de M ghinde, după care va reveni în vizuină. Veverițele vor efectua alternativ fiecare câte K ture, prima
care începe fiind Scratte.

Supărat că la concurs nu va începe primul, Scrat decide să se antreneze separat și să vadă câte ghinde ar culege în K
ture, dacă ar fi singur

Să se realizeze un program care determină:

1. Câte ghinde culege Scrat în timpul antrenamentului;
2. Câte ghinde a cules fiecare veveriță pe durata concursului.

Avem o jucărie formată din NxN pătrate de latură 1 dispuse ca într-o matrice cu N linii și N coloane. Liniile și coloanele matricei sunt numerotate de la 1 la N, iar N este mereu impar. Pătrățelele pot fi albe și le vom codifica 0, sau negre și le codificăm 1. Împărțim matricea în zone concentrice astfel: zona 1 este formată din linia 1, coloana N, linia N și coloana 1; zona 2 este formată din linia a doua, coloana N-1, linia N-1, coloana 2 etc. Sunt [N/2] astfel de zone. În mijlocul matricei este, evident, un singur element, N fiind impar. Asupra oricărei zone putem aplica o operație de rotire, doar spre stânga.

Dată fiind codificarea jucăriei, precum și “lungimea” maximă permisă pentru o rotire în oricare zonă, să se determine numărul de posibilități de a aplica rotiri asupra zonelor așa încât să rezolvăm jucăria. Evident, unei zone i se poate aplica o singură rotire, de lungime cuprinsă între 0 și valoarea maximă permisă.

Se consideră un șir de N numere naturale nenule ordonate crescător a[1]≤a[2]≤…≤a[N]. În legătură cu acest șir de numere ne interesează perechile de poziții (i,j) cu 1≤i<j≤N și a[i]≠a[j] sau ne interesează suma elementelor anumitor secvențe.

Se cere să se scrie un program care să citească un număr C reprezentând tipul cerinței, un șir de N numere naturale nenule ordonate crescător a[1]≤a[2]≤...≤a[N] și T perechi de numere naturale (p[k],q[k]) cu 1≤p[k]<q[k]≤N și 1≤k≤T și apoi:

(1) Dacă C=1, atunci trebuie să se determine pentru fiecare pereche dată de numere naturale (p,q) suma a[p]+a[p+1]+...+a[q].
(2) Dacă C=2, atunci trebuie să se determine pentru fiecare pereche dată de numere naturale (p,q) numărul de perechi (i,j) care respectă simultan condițiile p≤i<j≤q și a[i]≠a[j].

Se consideră două șiruri de numere naturale, ambele de lungime n, a=(a[1],a[2],...,a[n]) și b=(b[1],b[2],...,b[n]). Se știe că elementele din cele două șiruri sunt numere naturale, nu neapărat distincte, din mulțimea {1,2,…,n}. Cu cele două șiruri se poate face următoarea operație: se aleg doi indici i și j, cu 1≤i≤j≤n, apoi prin interschimbarea secvențelor a[i],a[i+1],...,a[j] cu b[i],b[i+1],...,b[j] se obțin șirurile:

• a[1], a[2], ...,a[i-1], b[i],b[i+1],…, b[j], a[j+1],a[j+2], …, a[n] și
• b[1], b[2], ...,b[i-1], a[i], a[i+1],…, a[j], b[j+1],b[j+2], …, b[n].

Dacă măcar unul din șirurile obținute este permutare a mulțimii {1,2,…,n}, atunci spunem că s-a obținut un mixperm.

Să se determine în câte moduri se poate obține un mixperm.

Dorel și-a achiziționat o fermă cu n plantații și o mașină de transport cu o capacitate c, pentru transportul de îngrășăminte la toate plantațiile. Îngrășămintele se află într-un depozit, în cantitate suficientă pentru scopul propus. Plantațiile și depozitul sunt dispuse sub forma unui cerc. Există drumuri doar între plantația i și plantația i+1 (1≤i≤n-1), precum și între depozit și plantația 1 și depozit și plantația n, ca în figură.

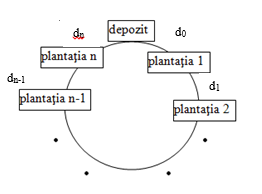
La o plantație i se poate ajunge de la depozit trecând prin plantațiile 1, 2,…, i-1 sau prin plantațiile n, n-1, …, i+1, alegerea făcându-se în funcție de traseul cel mai scurt. Se cunosc aceste distanțe, precum și cantitatea de îngrășăminte necesară pentru fiecare plantație. La fiecare încărcare, Dorel ia din depozit exact cantitatea c. Dorel vrea să-și organizeze bine munca la fermă și să consume cât mai puțină benzină prin alegerea celor mai scurte trasee de parcurs. Plantațiile trebuie să fie aprovizionate obligatoriu în ordinea următoare: mai întâi plantația 1, apoi plantația 2, plantația 3,…, plantația n. În plus, și-a propus să încarce o nouă cantitate de îngrășământ doar după ce a folosit toată cantitatea încărcată anterior. Transportarea îngrășămintelor pe plantații se face deci, începând cu plantația 1. După ce se transportă toată cantitatea necesară pentru această plantație, se trece la plantația 2, și tot așa în ordine la 3, 4 etc. până se deservește ultima plantație. Dacă după ce s-au transportat îngrășămintele necesare pentru plantația i în mașină au mai rămas încă îngrășăminte, acestea trebuie utilizate în continuare pentru alte plantații, alese în ordinea impusă (începând cu plantația i+1, apoi i+2 etc.), până se epuizează toată cantitatea transportată de mașină. Astfel, dacă de la plantația i trebuie să ajungă la plantația i+1, va alege cel mai scurt traseu dintre traseul direct de la plantația i la i+1 și traseul care trece prin plantațiile i-1, i-2, …, 1, depozit, n, n-1, …, i+1. La final, mașina trebuie să se întoarcă la depozit, goală sau cu cantitatea rămasă după aprovizionarea cu îngrășăminte a plantației n.

Ajutați-l pe Dorel să calculeze distanța parcursă pentru a transporta îngrășăminte la toate cele n plantații, conform cerințelor.