Algoritmul lui Lee

Algoritmul lui Lee este folosit pentru determinarea ieșirii dintr-un labirint sau în alte probleme similare cu aceasta.

Considerăm un labirint reprezentat printr-o matrice cu n linii și m coloane, în care elementele egale cu 0 reprezintă camere libere, iar cele egale cu 1 reprezintă camere blocat. Un mobil se deplasează prin labirint, trecând dintr-o cameră în alta dacă acestea se învecinează pe linie sau pe coloană. Determinați numărul minim de pași pe care îi face mobilul pentru a ieși din labirint (a ajunge pe chenarul matricei).

Pentru rezolvarea problemei procedăm astfel:

• marcăm în matrice elementele libere cu 0, iar obstacolele cu -1 (valorile pozitive sunt folosite în alt scop)
• marcăm poziția de start cu 1
• pentru fiecare k=1,2,3,...
  • analizăm elementele marcate cu valoarea k și marcăm cu k+1 toți vecinii săi care sunt liberi și nemarcați
  • dacă pentru un anumit k nu găsim niciun element egal cu k, ne oprim

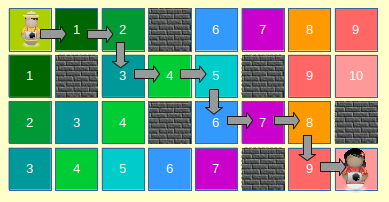
Lee cu coadă

Dacă pentru fiecare k parcurgem toate elementele matricei labirint pentru a identifica elementele egale cu k, algoritmul de mai sus este neeficient.

O soluție mult mai bună este să folosim o coadă:

• marcăm poziția de început cu 1 și o adăugăm în coadă
• expandăm coada. Cât timp coada este nevidă:
  • scoatem din coadă un element, cu coordonatele (i,j)
  • analizăm vecinii acestuia:
    • dacă vecinul curent (iv,jv) este liber și nemarcat, îl marcăm în matrice cu o valoare mai mare cu 1 decât elementul (i,j) – A[iv][jv] = A[i][j] + 1; – și îl adăugăm în coadă.

Implementare C++

Pentru mai multe modalități de implementare a cozii vezi articolul Fill cu coadă. În continuare vom folosi varianta cu containerul din STL.

void Lee(int istart ,int jstart)
{
    queue<pair<int,int>> Q;
    //initializare coada
    Q.push(make_pair(istart , jstart));
    //marcare pozitie de start
    A[istart][jstart] = 1;
    while(! Q.empty()) // cat timp coada este nevida
    {   
        int i = Q.front().first, j = Q.front().second; // determinam elementul de la inceputul cozii
        for(int k = 0 ; k < 4 ; k ++)
        {
            int iv = i + di[k], jv = j + dj[k]; // coordonatele vecinului
            if(iv >= 1 && iv <= n && jv >= 1 && jv <= m // element în matrice
                && A[iv][jv] == 0) // element liber si nemarcat
            {
                // marcam elementul vecin cu o valoare mai mare
                A[iv][jv] = A[i][j] + 1;
                // il adaugam in coada
                Q.push(make_pair(iv , jv));
            }
        }
        Q.pop(); // eliminam din coada
    }
}

Reconstituirea traseului

În unele probleme se dau două poziții în matricea labirint, (istart,jstart) și (istop,jstop) și se cere determinarea celui mai scurt traseu de la poziția (istart,jstart) la poziția (istop,jstop).

Operația se va realiza începând de la poziția finală spre cea inițială. Dacă poziția curentă a traseului are coordonatele (i,j), atunci poziția de dinainte va fi acel vecin (iv,jv) pentru care A[i][j] == A[iv][jv] + 1. Dacă sunt mai mulți asemenea vecini, oricare dintre ei este corect.

Deoarece elementele traseului se determină în ordine inversă, nu putem să afișăm direct coordonatele elementelor de pe traseu. Avem două soluții:

• să reconstituim traseul folosind un subprogram recursiv, care să aibă ca parametri coordonatele elementului curent, autoapelul să se facă pentru coordonatele vecinului aflat în traseul determinat înaintea elementului curent, iar afișarea să se facă la revenirea din autoapel;
• să reconstitui traseul iterativ și să memorăm coordonatele elementelor de pe traseu într-o structură corespunzătoare (tablou unidimensional de structuri, vector din STL, pereche de tablouri unidimensionale), iar la final să afișam elementele structurii de date în ordine inversă.

Reconstituire recursivă

void Traseu(int i, int j , int lg)
{
    if(A[i][j] == 1)
    {
        cout << lg << "\n";
        cout << i << " " << j << "\n";
    }
    else
    {
        int p = -1;
        for(int k = 0 ; k < 4 && p == -1 ; k ++)
            if(A[i][j] == A[i+di[k]][j+dj[k]] + 1)
                p = k;
        Traseu1(i + di[p] , j + dj[p] , lg + 1);
        cout << i << " " << j << "\n";
    }
}

Funcția C++ de mai sus afișează mai întâi lungimea traseului, apoi coordonatele elementelor de pe traseu. Desigur, lungimea traseului putea fi determinată în mod direct, din matrice. Apelul principal va fi:

Traseu(istart , jstart , 1);

Reconstituire nerecursivă

void Traseu2(int istop, int jstop)
{
    vector<pair<int,int>> V;
    int i = istop , j = jstop;
    V.push_back(make_pair(i , j));
    do
    {
        int p = -1;
        for(int k = 0 ; k < 4 && p == -1 ; k ++)
            if(A[i][j] == A[i+di[k]][j+dj[k]] + 1)
                p = k;
        i = i + di[p] , j = j + dj[p];
        V.push_back(make_pair(i , j));
    }
    while(A[i][j] != 1);
    cout << V.size() << '\n';
    for(vector<pair<int,int>>::reverse_iterator I = V.rbegin() ; I != V.rend() ; I ++)
        cout << I->first << " " << I->second << '\n';
}

Pentru memorarea coordonatelor elementelor de pe traseu am folosit un vector din STL. Bineînțeles, am fi putut folosi și un tablou standard C și, de asemenea, am fi putut parcurge vectorul cu un indice în loc de iterator.