Arbori binari

Definiție și proprietăți

Definiție. Se numește arbore binar un arbore cu rădăcină în care fiecare nod are cel mult doi descendenți direcți: descendentul stâng și descendentul drept.

Exemplu.

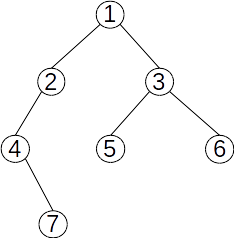
În arborele de mai sus:

nodul 1 este rădăcina;
rădăcina are doi descendenți direcți (fii): 2 este descendent stâng a lui 1, iar 3 este descendent drept;
nodul 2 are un singur descendent, pe 4. Acesta este descendent stâng al lui 2;
similar, 7 este descendent drept al lui 4;
nodurile 5, 6 și 7 sunt noduri terminale (frunze).

Observație. Dacă un nod are un singur descendent acesta va fi descendent stâng sau drept – acest lucru trebuie să fie precizat. Cei doi arbori de mai jos sunt considerați distincți.

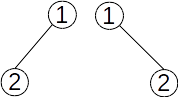
O altă definiție, recursivă, a arborelui binar este următoarea: Un arbore binar este o mulțime finită de noduri, astfel:

există un nod special, numit rădăcina arborelui;
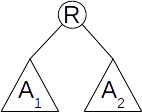
celelalte noduri sunt grupate în două submulțimi disjuncte \(A_1\) și \(A_2\), fiecare dintre ele fiind la rândul lor arbori binari. Arborii \(A_1\) și \(A_2\) reprezintă subarborele stâng, respectiv subarborele drept, al rădăcinii.

Această definiție recursivă este utilă deoarece foarte multe probleme cu arbori binari constau în prelucrarea nodurilor din arbore: a rădăcinii și a celor doi subarbori, în mod recursiv, prin metoda Divide et Impera.

Proprietății ale arborilor binari

Fiecare nivel i=0,1,2,... dintr-un arbore binar conține cel mult 2ⁱ noduri.
Un arbore binar de înălțime h conține cel mult 2^h+1-1 noduri. Demonstrația se bazează pe afirmația anterioară.
Într-un arbore cu n noduri și înâlțime h avem relația \( h \geq \log_{2}{(n+1)} -1 \).
Dacă într-un arbore binar numărul nodurilor terminale este a, iar c este numărul nodurilor care au exact 2 fii, atunci a = c + 1.

Tipuri speciale de arbori binari

Arbore binar strict

Definiție: Se numește arbore binar strict un arbore binar în care fiecare nod, cu excepția celor terminale, are exact doi descendenți.

Exemplu:

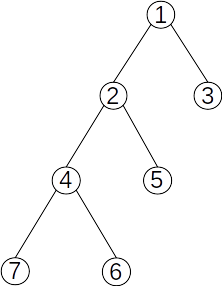
Proprietăți:

Un arbore binar strict cu \(k\) noduri terminale are \(n = 2 \cdot k – 1\) noduri.
Un arbore binar strict are număr impar de noduri.

Arbore binar plin

Definiție: Se numește arbore binar plin un arbore binar în care fiecare nivel \( k \in \left\{ 0 , 1, 2, \cdots, h \right\} \), unde \(h\) este înălțimea arborelui, conține \(2^k\) noduri.

Exemplu:

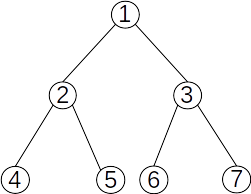
Proprietăți:

Arborele binar plin este un caz particular de arbore binar strict, în care toate nodurile terminale sunt situate pe același nivel.
Un arbore binar plin cu \(k\) noduri terminale are \(n = 2 \cdot k – 1\) noduri.
Un arbore binar plin cu înălțimea \(h\) are \(2^h-1\) noduri.

Arbore binar complet

Definiție: Se numește arbore binar complet un arbore binar în care fiecare nivel \( k \in \left\{ 0 , 1, 2, \cdots, h – 1 \right\} \), unde \(h\) este înălțimea arborelui, conține \(2^k\) noduri, iar nivelul \(k\) conține eventual mai puțin de \(2^h\) noduri, acestea fiind grupate de regulă în partea stângă.

Exemplu:

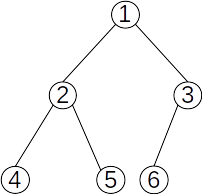
Observație: Arborele binar plin este și arbore binar complet.

Reprezentarea arborilor binari

Arborii binari se pot reprezenta fie prin referințe ascendente, fie prin referințe descendente, fie combinând cele două variante.

Reprezentarea prin referințe ascendente

În cazul reprezentării prin referințe ascendente, pentru fiecare nod din arbore trebuie să se cunoască:

nodul părinte
ce fel de descendent este (stâng sau drept).

Pentru memorarea informațiilor, considerând nodurile numerotate începând cu 1, putem folosi două tablouri: Tata[] și Tip[], unde Tata[k] reprezintă nodul părinte al lui k sau 0 dacă k este chiar rădăcina arborelui, iat Tip[k] este 0, dacă k este rădăcina arborului (caz în care nu are părinte), respectiv -1 dacă k este descendent stâng al lui Tata[k] sau 1 dacă k este descendent drept al lui Tata[k].

Exemplu.

Pentru arborele de mai sus, cele doua tablouri sunt:

`k`	`1`	`2`	`3`	`4`	`5`	`6`	`7`
`Tata[k`]	`0`	`1`	`1`	`2`	`3`	`3`	`4`
`Tip[k`]	`0`	`-1`	`1`	`-1`	`-1`	`1`	`1`

Reprezentarea prin referințe descendente

În cazul reprezentării prin referințe descendente, trebuie să fie cunoscută rădăcina arborelui binar, iar pentru celelalte noduri din arbore, trebuie să se cunoască fiul stâng și fiul drept.

Această reprezentare se poate face cu ajutorul tablourilor sau prin intermediul alocării dinamice.

Reprezentarea cu tablouri

Dacă folosim tablouri, vom avea nevoie de două tablouri, st[] (de la stânga) și dr[] (de la dreapta). Considerând nodurile numerotate de la 1 la n:

st[k] reprezintă numărul de ordine al nodului care este descendent stâng al lui k, sau 0 dacă k nu are descendent stâng;
dr[k] reprezintă numărul de ordine al nodului care este descendent drept al lui k, sau 0 dacă k nu are descendent drept.

Exemplu.

Pentru arborele de mai sus, cele doua tablouri sunt:

`k`	`1`	`2`	`3`	`4`	`5`	`6`	`7`
`st[k`]	`2`	`4`	`5`	`0`	`0`	`0`	`0`
`dr[k`]	`3`	`0`	`6`	`7`	`0`	`0`	`0`

Cunoscând valorile din cele două tablouri putem identifica rădăcina ca nodul care nu apare nici în st[], nici în dr[]. În exemplul de mai sus acesta este 1.

Reprezentarea folosind alocarea dinamică

Pentru fiecare nod al arborelui se crează o variabilă dinamică de tip structură, în care se vor memora următoarele câmpuri:

numărul nodului, sau orice informație utilă despre nod
două câmpuri de legătură, de tip pointer, reprezentând adresa nodului care este descendent stâng, respectiv adresa nodului care este descendent drept, sau NULL dacă nodul nu are descendent stâng (sau drept).

Următoarea secvență C/C++ definește structura:

struct nod{
	int info;
    nod * st, * dr;
};

Pentru operațiile cu arborele reprezentat astfel este necesar să cunoaștem adresa nodului rădăcină:

nod * R;

Pornind de la nodul rădăcină pot fi parcurse toate nodurile din arbore, pentru a efectua diverse operații cu acestea.

Crearea arborilor binari

Pentru a crea un arbore binar trebuie cunoscute pentru fiecare nod:

informația utilă memorată în acel nod
nodurile descendenților stâng și drept, dacă există

În funcție de reprezentarea folosită, mecanismul creării poate avea mai multe forme.

Crearea arborilor binari folosind reprezentarea statică

În cazul reprezentării statice pot fi citite numărul de noduri n și elementele tablourilor st[] și dr[], ca în exemplul următor:

// variabilele n, st[] si dr[] sunt considerate globale

void Citire()
{
    cin >> n;
    for(int i = 1 ; i <= n ; i ++)
        cin >> st[i];
    for(int i = 1 ; i <= n ; i ++)
        cin >> dr[i];
}

În numeroase probleme este necesară identificarea nodului rădăcină, folosind informațiile din cele două tablouri.

Determinarea rădăcinii se poate face ținând cont de faptul că ea nu este descendent al niciunui nod din arbore, deci nu va apărea în cele două tablouri:

int Radacina()
{
    int v[101] = {0};
    for(int i = 1 ; i <= n ; i ++)
    {
        if(st[i] != 0)
            v[st[i]] = 1;
        if(dr[i] != 0)
            v[dr[i]] = 1;
    }
    for(int i = 1 ; i <= n ; i ++)
        if(v[i] == 0)
            return i;
    return 0;
}

Crearea arborilor binari folosind reprezentarea dinamică

Reprezentarea dinamică unui arbore impune ca operațiile cu nodurile arborelui, inclusiv crearea, să se realizeze pornind de la rădăcină și continuând pe rând cu cei doi subarbori. Tehnica folosită este recursivitatea: pentru toți arborii (arborele initial și subarborii) realizăm aceleași operații – prelucrăm rădăcina și continuăm cu cei doi subarbori.

Schema folosită în funcția Creare din programul de mai jos este următoarea:

funcția primește ca parametru un pointer, inițial NULL. Crează arborele (subarborele) și îl întoarce având ca valoare adresa rădăcinii;
pentru fiecare apel (autoapel):
- citim informația utilă din nodul curent – rădăcina arborelui (subarborelui);
- dacă nodul curent are descendent stâng, continuăm cu acesta
- dacă nodul curent are descendent drept, continuăm cu acesta

Pentru afișarea arborelui folosim funcția Afisare care procedează similar:

are ca parametru adresa rădăcinii sau NULL
afișează rădăcina (informația utilă din rădăcină)
continuă recursiv cu subarborele stâng
continuă recursiv cu subarborele drept

#include <iostream>

using namespace std;

int n , st[101], dr[101];

struct nod {
	int info;
	nod * st, * dr;
};

void Creare(nod * & r, int x)
{
    if(x != 0)
    {
		r = new nod;
		r->info = x;
		r->st = r->dr = NULL;
		int y;
		cout << "st[" << x << "]="; cin >> y;
		Creare(r -> st , y);
		cout << "dr[" << x << "]="; cin >> y;
		Creare(r -> dr , y);;
	}
}

void Afisare(nod * r)
{
    if(r != NULL)
    {
		cout << r->info << " ";
		Afisare(r->st);
		Afisare(r->dr);
	}
}

int main()
{
	nod * R = NULL;
	int x;
	cout << "Eticheta radacinii: "; cin >> x;
    Creare(R , x);
    Afisare(R);
    return 0;
}

Parcurgerea arborilor binari

Pentru a prelucra un arbore este necesar ca nodurile sale să fie vizitate. La fel ca în cazul grafurilor (ceea ce și sunt de fapt arborii binari), ei pot fi parcurși în lățime sau în adâncime, a doua metodă fiind de regulă folosită.

Parcurgerea începe din rădăcină.

În funcție de ordinea în care se vizitează nodurile avem următoarele parcurgeri:

parcurgerea în inordine – SRD – se parcurge mai întâi subarborele stâng (S), apoi rădăcina (R), apoi subarborele drept (D);
parcurgerea în preordine – RSD – se parcurge mai întâi rădăcina (R), apoi subarborele stâng (S), apoi subarborele drept (D);
parcurgerea în postordine – SDR – se parcurge mai întâi subarborele stâng (S), apoi subarborele drept (D), apoi rădăcina (R).

Observație: În programul de mai sus, crearea și afișarea arborelui se fac cu ajutorul parcurgerii, mai precis a parcurgerii în preordine.

Exemplu

Pentru arborele de mai sus, ordinea de parcurgere este:

Inordine – SRD: 4 7 2 1 5 3 6
Preordine: RSD 1 2 4 7 3 5 6
Postordine: SDR 7 4 2 5 6 3 1

Deoarece parcurgerea începe din rădăcină și continuă cu nodurile descendent (cu subarborii stâng și drept), reprezentarea folosită este cea cu referințe descendente.

Programul C++ următor conține subprograme care implementează cele trei modalități de parcurgere pentru afisarea nodurilor din arbore. Reprezentarea arborelui este prin tablourile st[] și dr[]. Datele de intrare se citesc de la tastatură: mai întâi se citește numărul de noduri, n, apoi elementele vectorului st[], apoi elementele vectorului dr[].

#include <iostream>

using namespace std;

int n , st[101], dr[101];

void Citire()
{
    cin >> n;
    for(int i = 1 ; i <= n ; i ++)
        cin >> st[i];
    for(int i = 1 ; i <= n ; i ++)
        cin >> dr[i];
}

int Radacina()
{
    // radacina este un nod intre 1 și n care nu apare în tablourile st[] și dr[]
    int v[101] = {0};
    for(int i = 1 ; i <= n ; i ++)
    {
        if(st[i] != 0)
            v[st[i]] = 1;
        if(dr[i] != 0)
            v[dr[i]] = 1;
    }
    for(int i = 1 ; i <= n ; i ++)
        if(v[i] == 0)
            return i;
    return 0;
}

void Inordine(int x)
{
    if(x != 0)
    {
        Inordine(st[x]);
        cout << x << " ";
        Inordine(dr[x]);
    }
}

void Preordine(int x)
{
    if(x != 0)
    {
        cout << x << " ";
        Preordine(st[x]);
        Preordine(dr[x]);
    }
}

void Postordine(int x)
{
    if(x != 0)
    {
        Postordine(st[x]);
        Postordine(dr[x]);
        cout << x << " ";
    }
}

int main()
{
    Citire();
    int R = Radacina();
    Inordine(R); 
    cout << endl;
    Preordine(R); 
    cout << endl;
    Postordine(R); 
    cout << endl;
    return 0;
}

Programul C++ următor conține subprograme care implementează cele trei modalități de parcurgere pentru afisarea nodurilor din arbore, reprezentarea acestuia fiind cea dinamică.

#include <iostream>

using namespace std;

int n , st[101], dr[101];

struct nod {
	int info;
	nod * st, * dr;
};

void Creare(nod * & r, int x)
{
    if(x != 0)
    {
		r = new nod;
		r->info = x;
		r->st = r->dr = NULL;
		int y;
		cout << "st[" << x << "]="; cin >> y;
		Creare(r -> st , y);
		cout << "dr[" << x << "]="; cin >> y;
		Creare(r -> dr , y);;
	}
}


void Preordine(nod * r)
{
    if(r != NULL)
    {
		cout << r->info << " ";
		Preordine(r->st);
		Preordine(r->dr);
	}
}

void Inordine(nod * r)
{
    if(r != NULL)
    {
		Inordine(r->st);
		cout << r->info << " ";
		Inordine(r->dr);
	}
}

void Postordine(nod * r)
{
    if(r != NULL)
    {
		Postordine(r->st);
		Postordine(r->dr);
		cout << r->info << " ";
	}
}

int main()
{
	nod * R = NULL;
	int x;
	cout << "Eticheta radacinii: "; cin >> x;
    Creare(R , x);
    Preordine(R); cout << endl;
    Inordine(R);  cout << endl;
    Postordine(R); cout << endl;
    return 0;
}

Ștergerea arborilor binari

Ștergerea arborilor binari este necesară cu precădere în cazul reprezentării dinamice a acestora.

Ștergerea se va face nod cu nod, folosind parcurgerea în postordine: parcurgem subarbore stâng, apoi subarborele drept, apoi prelucrăm rădăcina. În acest fel la ștergerea nodului rădăcină cei doi subarbori sunt deja șterși.

Funcția C++ de mai jos șterge arborele binar pentru care adresa rădăcinii este transmisă ca parametru. Acesta parametru este de intrare-ieșire: intră cu adresa rădăcinii și iese cu valoarea NULL – arborele a fost șters.

void Stergere(nod * & R)
{
	if(R != NULL)
    {
    	Stergere(R->st);
        Stergere(R->dr);
        delete R;
        R = NULL;
    }
}

Funcția de mai sus poate fi utilizată și pentru ștergerea unui subarbore dintr-un arbore dat. Este însă important ca parametrul să fie câmpul st sau dr din nodul părinte, nu un pointer oarecare care să memoreze adresa rădăcinii subarborelui.

Exemplu: Considerăm un arbore binar pentru care adresa rădăcinii este memorată în pointerul R. Dorim să ștergem subarborele stâng al rădăcinii, care are adresa în R->st.

Următoarea secvență este corectă.

Stergere(R->st);

Următoarea secvență este greșită. De ce?

nod * p = R->st;
Stergere(p);