Folosim următoarele structuri de date:
- un vector
d[], în cared[k]reprezintă costul minim curent al drumului de la nodul sursăs=1lak; - un vector caracteristic
F[], în careF[k]=1dacă pentru nodulks-a determinat costul minim final, respectivF[k]=0dacă pentru nodulknu s-a determinat (încă) acest cost;
Graful dat este:
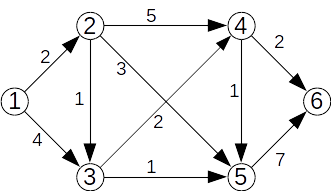
Pasul 0: Initializăm cei doi vectori, ca mai jos. Inițial în mulțimea F se află doar nodul sursă s=1.
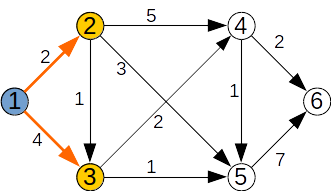
| k | 1 | 2 | 3 | 4 | 5 | 6 |
| F[k] | 1 | 0 | 0 | 0 | 0 | 0 |
| d[k] | 0 | 2 | 4 | ∞ | ∞ | ∞ |
Pasul 1: Alegem un vârf k din afara lui F, pentru care d[k] este finit și minim. Acesta este k=2. Îl adăugăm în F și analizăm nodurile x pentru care (k,x) este arc. Se vor relaxa nodurile 3 4 5.
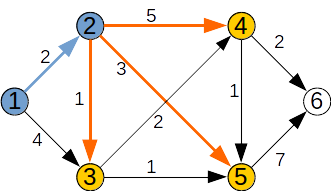
| k | 1 | 2 | 3 | 4 | 5 | 6 |
| F[k] | 1 | 1 | 0 | 0 | 0 | 0 |
| d[k] | 0 | 2 | 3 | 7 | 5 | ∞ |
Pasul 2: Alegem un vârf k din afara lui F, pentru care d[k] este finit și minim. Acesta este k=3. Îl adăugăm în F și analizăm nodurile x pentru care (k,x) este arc. Se vor relaxa nodurile 4 5.
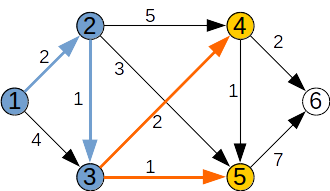
| k | 1 | 2 | 3 | 4 | 5 | 6 |
| F[k] | 1 | 1 | 1 | 0 | 0 | 0 |
| d[k] | 0 | 2 | 3 | 5 | 4 | ∞ |
Pasul 3: Alegem un vârf k din afara lui F, pentru care d[k] este finit și minim. Acesta este k=5. Îl adăugăm în F și analizăm nodurile x pentru care (k,x) este arc. Se va relaxa nodul 6.
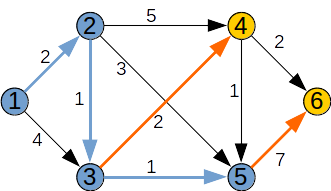
| k | 1 | 2 | 3 | 4 | 5 | 6 |
| F[k] | 1 | 1 | 1 | 0 | 1 | 0 |
| d[k] | 0 | 2 | 3 | 5 | 4 | 11 |
Pasul 4: Alegem un vârf k din afara lui F, pentru care d[k] este finit și minim. Acesta este k=4. Îl adăugăm în F și analizăm nodurile x pentru care (k,x) este arc. Se va relaxa nodul 6.
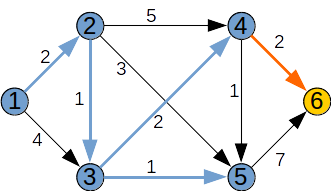
| k | 1 | 2 | 3 | 4 | 5 | 6 |
| F[k] | 1 | 1 | 1 | 1 | 1 | 0 |
| d[k] | 0 | 2 | 3 | 5 | 4 | 7 |
Pasul 5: Alegem un vârf k din afara lui F, pentru care d[k] este finit și minim. Acesta este k=6. Îl adăugăm în F și analizăm nodurile x pentru care (k,x) este arc. Nu mai există asemenea arce, niciun nod nu se mai relaxează.
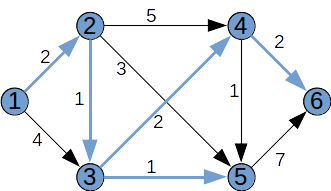
| k | 1 | 2 | 3 | 4 | 5 | 6 |
| F[k] | 1 | 1 | 1 | 1 | 1 | 1 |
| d[k] | 0 | 2 | 3 | 5 | 4 | 7 |
Algoritmul lui Dijkstra s-a încheiat. Valorile finale din vectorul d[] – distanțele minime de la nodul s=1 la toate celelalte sunt cele de mai sus.