Acest site foloseşte cookies. Navigând în continuare, vă exprimaţi acordul asupra folosirii cookie-urilor.
Articole
tema 18.10.2022
2022-10-18
|
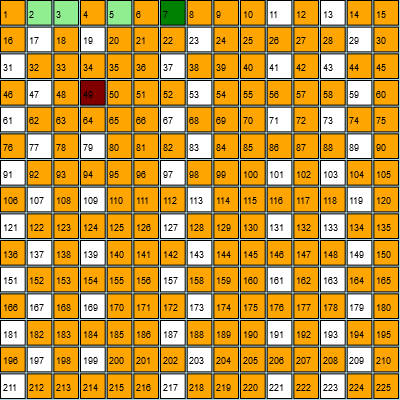
Ciurul lui Eratostene
2023-06-04
|
Aplicații ale descompunerii în factori primi
2022-02-19
|
Divizibilitate
2020-01-06
|