Lista de probleme 6
#740
Horse
Se consideră o tablă de şah cu n linii şi n coloane, şi n=4k+1. Liniile acestei table sunt numerotate de sus în jos începând cu linia 1, iar coloanele sunt numerotate de la stânga la dreapta începând cu 1. În fiecare dintre câmpurile acestei table se scrie câte un număr natural din mulţimea {1, 2, …, n2} după următoarele reguli:
a) se porneşte din colţul aflat în poziţia stânga sus al tablei şi se avansează utilizând săritura calului
b) se merge orizontal către dreapta şi în continuare, pe chenarul format din primele două linii, primele două coloane, ultimele două linii şi ultimele două coloane, în sensul acelor de ceasornic;
c) se efectuează mai multe tururi ale tablei, până ce se umple întregul chenar, fără să se sară de două ori în aceeaşi căsuţă, fără să se sară în afara acestui chenar şi fără să rămână vreun câmp liber;
d) din poziţia finală în care s-a ajuns, trebuie să fie posibilă săritura în colţul din stânga sus al pătratului rămas neacoperit;
e) se continuă deplasarea în interiorul pătratului rămas neacoperit, folosind regulile a), b), c), d) până ce se ajunge la pătratul interior de latură 1 care va conţine valoarea n2.
Cunoscând valoarea lui n ce reprezintă dimensiunea tablei şi un număr p, să se determine linia şi coloana căsuţei din tabelă unde este scris numărul p, după regulile de mai sus.
Lot Juniori, Bistrita, 2009
- Fișiere
- Zoltan Szabo
- concurs
- Clasa 9 Probleme diverse Probleme diverse
#741
Mins
În planul xOy se desenează un dreptunghi cu laturile paralele cu axele de coordonate. Coordonatele vârfurilor din stânga-jos şi dreapta-sus ale dreptunghiului sunt: (0,0) şi (c,d). Fie P mulţimea punctelor situate în interiorul dreptunghiului, ale căror coordonate sunt numere naturale. Prin desenarea unui număr minim m de segmente de dreaptă, se uneşte vârful de coordonate (0,0) cu fiecare punct din mulţimea P. Astfel, fiecare punct din P va aparţine interiorului unui segment din cele m sau va fi o extremitate a unui segment din cele m.
Scrieţi un program care să citească numerele naturale c şi d, şi care să determine numărul minim m de segmente de dreaptă desenate.
Lot Juniori, Bistrita, 2009
- Fișiere
- Carmen Minca
- concurs
- Clasa 9 Probleme diverse Probleme diverse
- Eratostene
- Algoritmul lui Euclid
#742
Numar2
Fie un număr natural a având n cifre. Scrieţi un program care să determine un număr natural x cu proprietatea că este cel mai mic număr mai mare decât a, care are exact aceleaşi cifre ca şi numărul a.
Lot Juniori, Bistrita, 2009
- Fișiere
- concurs
- Clasa 9 Probleme diverse Probleme diverse
#743
Operatii
Fiind date două tablouri bidimensionale a şi b, cu m linii şi n coloane fiecare, definim următoarele operaţii:
1. suma tablourilor a şi b, ca fiind un tablou c cu m linii şi n coloane, în care fiecare element este egal cu suma elementelor de pe aceeași linie şi aceeași coloană din a şi b. În acest caz folosim operatorul +, adică c=a+b.
2. produsul tablourilor a şi b, ca fiind un tablou d cu m linii şi n coloane, în care fiecare element este egal cu produsul elementelor de pe aceeași linie şi aceeași coloană din a şi b. În acest caz folosim operatorul *, adică d=a*b. Dacă a şi b sunt tablouri identice (a şi b au elemente identice pe aceeaşi poziţie), atunci pentru d se mai foloseşte şi notaţia a2 sau b2.
De exemplu, pentru m=2, n=3 şi tablourile:
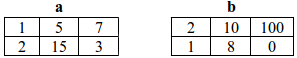
se obține:

Fiind dat un tablou bidimensional a, cu m linii, n coloane şi componente numere naturale dorim să determinăm un şir de tablouri bidimensionale: b1, b2, …, bk cu număr minim de termeni (k minim), cu proprietatea că a=b12+b22...+bk2.
Lot Juniori, Bistrita, 2009
- Fișiere
- Doru Popescu Anastasiu
- concurs
- Clasa 9 Probleme diverse Probleme diverse
#739
Cuburi1
Fie n cuburi de aceeaşi mărime, cu feţe colorate. Culorile sunt codificate prin câte o literă de la A la M. Pentru fiecare cub se cunosc culorile feţelor în ordinea: bază, capac, faţă frontală, faţă laterală dreapta, faţa din spate, faţă laterală stânga. Să se determine numărul maxim de cuburi care, răsturnate şi rotite convenabil, pot fi puse unul peste altul astfel încât să formeze un turn cu toate feţele uniform colorate (fiecare faţă a turnului sa fie de aceeaşi culoare, de la primul, până la ultimul cub al turnului).
Lot Juniori, Bistrita, 2009
- Fișiere
- Zoltan Szabo
- concurs
- Clasa 11 Probleme diverse Probleme diverse
#744
Rec
După strălucita victorie de la Austerlitz împotriva coaliţiei ruso-austriece, împăratul Napoleon Bonaparte doreşte să recompenseze N generali care s-au remarcat în luptă. Pentru aceasta, el dispune de o sumă în franci de valoare S. La festivităţile dedicate victoriei, cei N generali vor fi aliniaţi în ordinea descrescătoare a meritelor lor pe câmpul de luptă şi împăratul îi va chema pentru înmânarea recompensei în această ordine.
Bonaparte doreşte să împartă întreaga sumă astfel încât generalul cel mai merituos să primească suma cea mai mare şi oricare alt general să primească o sumă cel mult egală cu a generalului care a fost premiat anterior. De asemenea, generalul cu cel mai mic premiu nu trebuie să primească mai puţin de F franci.
Determinaţi numărul de variante distincte de acordare a recompenselor de către împăratul Napoleon.
Lot Juniori, Bistrita, 2009
- Fișiere
- Suzana Galatan
- concurs
- Clasa 11 Programare dinamică Probleme diverse de programare dinamică