Lista de probleme 2
#1643
Tromino
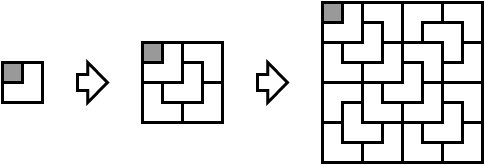
Bulbuka a primit de curând cadou un infinit de tromino-uri în formă de L. După ce s-a jucat un timp cu ele, a ajuns la următoarea concluzie: poate să acopere cu tromino-uri o tablă de dimensiuni 2Kx2K aproape complet (mai puţin un pătrăţel de dimensiune 1x1). Deşteapta de Bulbuka are un algoritm pentru asta: porneşte de la o configuraţie 2K-1x2K-1, o copiază de încă 3 ori, apoi roteşte 2 dintre copii şi la sfârşit, adaugă un tromino la mijloc (v-a făcut un desen mai jos, ca să înţelegeţi mai bine, pentru K = 1, 2 şi 3). Pornind de la o configuraţie de acest tip, ea a observat că poate roti la 90o câte un tromino, în sensul acelor de ceasornic sau invers, doar dacă după rotire încape înapoi pe tablă. Folosind astfel de rotaţii, pătrăţelul lipsă poate ajunge pe orice poziţie de pe tablă.
Bulbuka vă pune acum Q întrebări de tipul: care este numărul minim de rotaţii necesare pentru ca pătrăţelul lipsă să ajungă de la coordonatele (SR,SC) la coordonatele (FR,FC)?
Urmasii lui Moisil, 2016
- Fișiere
- Vlad Stoian
- concurs
- Clasa 9 Probleme diverse Probleme diverse
#1642
Culegere
Pădurea magică din Povestea lui Negrimon este situată pe un teren dreptunghiular care poate fi privit ca o matrice cu N linii, numerotate de la 1 la N şi M coloane, numerotate de la 1 la M. Putem spune că terenul este împărţit în N * M
parcele pătrate de latură 1. În pădure trăieşte şarpele Snake care, iniţial, este lung cât K parcele şi lat cât una singură. La începutul poveştii şarpele se află pe prima linie, pe parcelele de la 1 la K, capul fiind pe poziţia K şi orientat spre est.
Snake se deplasează cu o parcelă pe secundă. Astfel, după prima secundă, şarpele se va afla tot pe linia 1, deplasat cu o poziţie spre dreapta, mai exact capul va fi în parcela K + 1. Deplasarea se face simultan cu întreg corpul.
În pădure au loc E evenimente ce pot fi de tipurile următoare:
- Apariţia unui măr la secunda
stpe liniaxşi coloanay, care va dispărea la secundaen, dacă nu este mâncat până atunci de şarpe. Snake înghite mărul când capul său ajunge în parcela care îl conţine. Mărul dispare, desigur, iar corpul şarpelui creşte instantaneu cu o unitate care îi va fi adăugată la coadă şi va ocupa aceeaşi parcelă pe care s-a aflat coada (ultima porţiune din corp) la secunda anterioară înghiţirii mărului.
- Apariţia unui schimbător la secunda
stpe liniaxşi coloanay, care va dispărea la secundaenşi care are valoareav. Când capul şarpelui ajunge în parcela schimbătorului, direcţia ulterioară de deplasare va fi dată de valoareav ∈ {1, 2, 3, 4}cu semnificaţia:1Nord (sus);2Est (dreapta);3Sud (jos);4Vest (stânga).
Schimbătorul funcţionează astfel: de exemplu, dacă Snake se deplasează spre Est şi la o anumită secundă capul acestuia ajunge într-o parcelă unde se află un schimbător cu valoarea 1, la următoarea secundă capul se va afla în parcela situată deasupra schimbătorului şi în parcela schimbătorului se află prima porţiune din corpul şarpelui.
Schimbătorul dispare exact în secunda en iar până atunci rămâne în matrice indiferent de câte ori Snake trece prin parcela acestuia. Schimbătorul va acţiona doar când capul lui Snake ajunge în parcela lui şi nu va exista nicio situaţie în care să se schimbe direcţia în sens opus celei din care vine. De exemplu, dacă direcţia lui Snake este spre Est, nu va întâlni un schimbător cu valoarea 4, care l-ar întoarce spre Vest.
În fiecare secundă s, evenimentele se petrec în acestă ordine: dispar obiectele programate să dispară în secunda s, apar obiectele ce trebuie să apară în secunda s, Snake se deplasează cu o parcelă. Dacă printr-o combinaţie nefericită de mişcări, Snake se loveşte de propriul corp, el se blochează şi aşteptă serviciul de asistenţă a pădurii.
Deoarece Snake se află într-o pădure magică, deplasarea lui respectă reguli speciale: când capul este pe ultima coloană din matrice şi se mişcă spre Est, el reapare pe aceeaşi linie, dar pe prima coloană, trăgând corpul simultan. Analog şi pentru prima coloană, când se deplasează spre Vest, capul reapare pe aceeaşi linie dar pe ultima coloană. Dacă şarpele se află pe prima linie şi se deplasează spre Nord, mişcarea va continua pe ultima linie şi aceeaşi coloană din matrice. Analog pentru ultima linie, când Snake se deplasează spre Sud, capul reapare pe prima linie şi aceeaşi
coloană. Aceste mişcări au loc doar dacă Snake nu se blochează în propriul corp.
Povestea se termină în secunda în care apare oricare dintre situaţiile: Snake se loveşte de propriul corp, caz în care el rămâne BLOCAT; toate cele E evenimente s-au produs şi nu mai există niciun obiect în matrice pentru că toate au
dispărut, caz în care rămâne un şarpe LIBER.
Cerința: În funcţie de finalul poveştii, afişaţi starea lui Snake şi harta pădurii în secunda respectivă. Pe hartă trebuie să fie marcate parcelele ocupate de corpul lui Snake, inclusiv capul.
Urmasii lui Moisil, 2016
- Fișiere
- Stefan Negrus
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme diverse