Lista de probleme 28
Nivelul concursului: Național
http://oni.isjbrasov.ro/ http://oni2017.host4u.ro/
Grupe
Clasa a V-a Clasa a VI-a Clasa VII-a Clasa VIII-a Clasa a IX-a Clasa a X-a Clasele XI-XII Juniori Seniori
#2058
Submat
Se consideră o matrice A având N linii și N coloane. Elementele acesteia aparțin mulțimii {0,1,2}. Pe fiecare linie și pe fiecare coloană valorile elementelor sunt dispuse crescător.
Fie două elemente din matrice situate pe linia i1 și coloana j1 respectiv i2 și j2,unde i1≤i2 și j1≤j2. O submatrice a lui A, având colțurile stânga-sus şi dreapta-jos în (i1,j1) și (i2,j2), este formată din toate elementele situate pe linii cuprinse între i1 și i2, inclusiv, și coloane între j1 și j2, inclusiv. Numim submatrice constantă o submatrice a matricei A, având toate elementele egale.
Realizați un program care determină numărul maxim K de elemente pe care îl are o submatrice constantă a lui A și numărul submatricilor constante formate din K elemente.
ONIGIM 2017, Clasa a VII-a
- Fișiere
- Stelian Ciurea
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Probleme diverse
#2066
boats
Pe o foaie de matematică cu N pătrățele orizontale (pe aceeași linie) și M pătrățele verticale (pe aceeași coloană), Alex a pictat nave. Definim o navă linie (L) ca un set de pătrățele umbrite, consecutive pe un rând al foii de matematică. Definim o navă coloană (C) ca un set de pătrățele umbrite, consecutive pe o coloană a foii de matematică. Dimensiunea unei nave este egală cu numărul de pătrățele din care este formată. O navă formată dintr-un singur pătrățel nu este nici linie, nici coloană. Navele pot avea diferite dimensiuni. Două nave diferite nu se ating pe laturi sau colțuri, nu se suprapun și nu au pătrățele comune. Pe foaia de matematică sunt pictate doar nave de cele 3 tipuri: navă linie (L), navă coloană (C) sau navă pătrățel.
Cunoscându-se M, N și pictura lui Alex, scrieți un program care să determine:
- Numărul de nave formate doar dintr-un singur pătrățel;
- Numărul de nave linie și numărul de nave coloană, precum și dimensiunile acestora.
ONIGIM 2017, Clasa a VIII-a
- Fișiere
- Liliana Chira
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Probleme diverse
#2145
Soricel
Șoricelul Remy dorește să depoziteze cubulețele de cașcaval pe care le-a adunat. El a construit un depozit pe o suprafață dreptunghiulară și l-a compartimentat în N*M camere identice. În fiecare cameră șoricelul a depozitat o cantitate de cubulețe de cașcaval (ca în Figura A) și a stabilit că va mânca în fiecare zi câte un cubuleț de cașcaval din fiecare cameră în care există cașcaval. Planul său este stricat de John, șoricelul leneș din casa vecină, căruia nu-i place să-și strângă singur cașcaval, așa că s-a hotărât să fure din depozitul lui Remy. Pentru că John este pasionat de matematică s-a hotărât ca în fiecare seară, după ce vecinul său a terminat de mâncat, să se plimbe prin depozit și să fure tot cașcavalul din camerele în care găsește un număr pătrat perfect de cubulețe de cașcaval. John intră în depozit prin camera din colțul stânga sus, de coordonate (1,1), parcurge prima linie de la prima la ultima coloană, apoi a doua linie de la ultima coloană, până la prima și așa mai departe, până când termină de vizitat toate camerele (ca în Figura B).
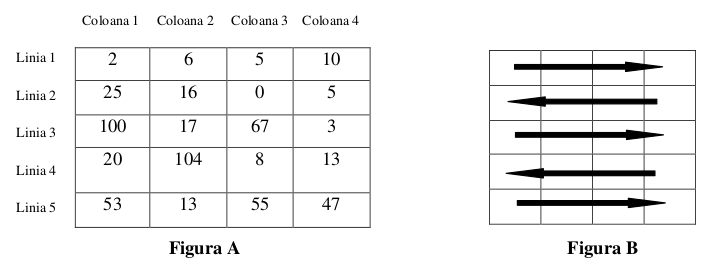
Scrieți un program care să determine:
- Numărul de zile în care se va goli depozitul lui Remy și câte camere va goli John în ziua
K. - Numărul maxim de camere consecutive golite de acesta într-o zi și ziua în care se va întâmpla acest lucru.
ONIGIM 2017, Clasa a VI-a
- Fișiere
- Flavius Boian
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Probleme diverse
#2156
Adlic
Pentru următorul an școlar admiterea celor N elevi în liceu se va face pe baza unor evaluări complexe. Fiecare dintre viitorii elevi ai clasei a IX-a va primi, în urma testelor și probelor pe care le va susține, un punctaj (număr natural nenul) cu care va participa la admiterea electronică.
Repartizarea fiecărui elev în clase se face în ordinea înscrierii respectând criteriile:
- Primul elev se repartizează în clasa cu numărul de ordine
1. - În clasa în care este repartizat un elev nu există, până la momentul repartizării sale, nici un punctaj mai mare decât al său.
- Numărul claselor să fie cât mai mic posibil.
Determinaţi:
- Punctajul primului elev care nu ar mai putea fi repartizat în prima clasă în condițiile în care toți elevii își doresc să fie repartizați în prima clasă(se aplică doar la cerința 1).
- Numărul claselor ce se vor forma respectând criteriile.
ONI 2017, Clasa a IX-a
- Fișiere
- George Vlad
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Parcurgerea vectorilor
- Cautare binara
#2045
Faleza
Acum iarna s-a terminat și, apropiindu-se sezonul de vară, gospodarii din orașul de pe malul fluviului doresc să pregătească faleza pentru a primi cum se cuvine turiștii. Faleza este sub formă dreptunghiulară cu lungimea de n metri și lățimea de 2 metri. În toamnă ea era pavată cu 2*n dale pătrate cu latura de un metru, lipite una de alta și care acopereau complet zona falezei. În urma iernii grele, unele dale s-au deteriorat și acum se dorește înlocuirea lor.Cum de multe ori oamenii fac treaba doar “pe jumătate”, gospodarii au hotărât să cheltuie cât mai puțin pentru reamenajarea falezei, așa că au decis că nu trebuie neapărat să înlocuiască toate dalele deteriorate, ci doar un număr minim dintre acestea astfel încât să fie posibil să se parcurgă faleza de la un capăt la altul pășind doar pe dale bune (nedeteriorate). De pe o dală pe alta se poate păși doar dacă ele au o latură comună.
Scrieţi un program care să determine numărul minim de dale deteriorate ce trebuie înlocuite astfel încât faleza să
poată fi parcursă de la un capăt la altul.
ONIGIM 2017
- Fișiere
- Marius Nicoli
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Parcurgerea vectorilor
#2046
carte2
În timpul activităților din “Săptămâna Altfel” elevii clasei a VII-a doresc să ajute la organizarea cărților din biblioteca școlii. Fiecare carte este etichetată cu un cod care este exprimat printr-un un șir de caractere distincte. Acestea pot fi cifrele 0, 1,..,9 și primele zece litere mici ale alfabetului englez a, b,..,j. Codul identifică în mod unic fiecare carte, adică nu vor exista două cărți cu același cod, dar şi genul literar din care acestea face parte. Cărțile din acelaşi gen literar au codul de identificare format din aceleaşi caractere, distincte, dispuse în altă ordine.
Numim coduri pereche două coduri de identificare care au același număr de caractere și care diferă printr-un
caracter. De exemplu, codurile 42a8 și 2c8a sunt coduri pereche. Pe de altă parte, codurile 42a8 și 248a,
respectiv 42ab și 248c, nu sunt coduri pereche.
Fiind dat șirul celor N coduri de identificare, scrieţi un program care să rezolve următoarele cerinţe:
- determină numărul de cărți din cel mai numeros gen literar și numărul de genuri literare care au acest număr maxim de cărți.
- determină numărul de coduri, din șirul celor
N, care sunt coduri pereche cu ultimul cod din șir
ONIGIM 2017, Clasa a VII-a
- Fișiere
- Adrian Pintea
- concurs
- Clasa 9 Probleme diverse Probleme diverse
#2047
ghinde
Scrat și Scratte sunt două veverițe devoratoare de ghinde. Ele trăiesc într-un stejar înalt și culeg ghinde din cele N ramuri ale acestuia. Veverițele vor organiza un concurs: cine culege cele mai multe ghinde în K ture. Într-o tură,
fiecare veveriță se va deplasa de la vizuină până la o ramură a stejarului, de unde va culege cât mai multe ghinde, dar
nu mai mult de M ghinde, după care va reveni în vizuină. Veverițele vor efectua alternativ fiecare câte K ture, prima
care începe fiind Scratte.
Supărat că la concurs nu va începe primul, Scrat decide să se antreneze separat și să vadă câte ghinde ar culege în K
ture, dacă ar fi singur
Să se realizeze un program care determină:
- Câte ghinde culege Scrat în timpul antrenamentului;
- Câte ghinde a cules fiecare veveriță pe durata concursului.
ONIGIM 2017, Clasa a VII-a
- Fișiere
- Mircea Rotar
- concurs
- Clasa 9 Probleme diverse Probleme diverse
#2147
z
Magazinul de jocuri a lansat cea mai recentă versiune a jocului Z, pentru a-i ajuta pe elevii din clasa a VIII-a să înțeleagă mai bine modul de identificare a coordonatelor unui punct din plan, într-un sistem de axe ortogonale.
Pe ecran este afișată o foaie de matematică și sistemul de axe ortogonale xOy. Succesiv, apar coordonatele întregi ale
unor puncte din plan. Jucătorul trebuie să marcheze pe foaie fiecare punct și să traseze un segment care să unească
punctul (cu excepția primului punct marcat) cu cel marcat anterior.
La sfârșitul jocului, jucătorul trebuie să numere de câte ori a trecut prin originea sistemului de coordonate O(0,0) și care este numărul maxim al semnelor Z distincte, formate cu puncte marcate.
Cunoscându-se n (numărul de puncte afișate succesiv pe ecran) și coordonatele celor n puncte din plan, să se scrie un program care determină:
- Numărul de treceri prin originea sistemului de coordonate.
- Numărul maxim al semnelor Z distincte, formate cu puncte marcate.
ONIGIM 2017, Clasa a VIII-a
- Fișiere
- Cristina Sichim
- concurs
- Clasa 9 Probleme diverse Probleme diverse
#2152
Arhipelag
În regiunea Ionia a lumii grecești antice, regiune ce corespunde teritoriului actual al Mării Egee, există mai multe insule. Harta mării este reprezentată de o matrice de dimensiuni N•M, având valori de 1 și 0, iar fiecare element din matrice reprezintă o zonă de dimensiune 1•1 din mare. Liniile matricei sunt numerotate de la 1 la N, de sus în jos, iar coloanele de la 1 la M, de la stânga la dreapta. Astfel, colțul din stânga sus al matricei este asociat zonei (1,1), iar colțul din dreapta jos corespunde zonei (N,M).
Un element care conține valoarea 0 reprezintă faptul că în acea zonă se află apă. O insulă este determinată
de un dreptunghi format în totalitate din valori de 1. Se garantează faptul că toate zonele care conțin valoarea 1
formează dreptunghiuri valide și că oricare două insule sunt separate de apă.
Ionienii, fiind oameni practici, doresc construirea unui far-bibliotecă (așezat pe o platformă 1•1), într-o zonă acoperită de apă. Poziția platformei va fi aleasă într-o celulă C astfel încât suma distanțelor dintre toate insulele și C să fie minimă. Distanța dintre o celulă C și o insulă este definită ca fiind minimul dintre distanțele Manhattan dintre C și fiecare celulă care aparține insulei (distanța poate trece atât prin alte insule, cât și prin zone acoperite de apă). Distanța Manhattan dintre două celule aflate pe linia x1 și coloana y1, respectiv pe linia x2 și coloana y2, este definită ca |x1 – x2| + |y1 – y2|, unde |x| reprezintă valoarea absolută a lui x.
ONI 2017, Clasa a IX-a
- Fișiere
- Mihai Enache
- concurs
- Clasa 9 Probleme diverse Probleme diverse
#2153
Mirror
Numim „oglinda” numărului natural nenul a, numărul b, obţinut prin modificarea fiecărei cifre din reprezentarea sa binară, de exemplu pentru a=22(10)=10110(2) se obţine 01001(2)= 9(10)=b.
Cunoscându-se numerele naturale N, K și cele N numere natural nenule, scrieți un program care:
- Transformă în baza doi termenii şirului dat obţinându-se un nou şir format din alipirea cifrelor binare. Din acest şir se vor determina și afișa, separate prin câte un spațiu, toate reprezentările în baza
10corespunzătoare secvenţelor alăturate de exactKcifre binare, parcurse de la stânga la drepta. Dacă ultima secvenţă nu are exactKcifre binare, atunci aceasta nu se va mai lua în considerare. - Să aplice
Ktransformări asupra şirului iniţial, înlocuind la fiecare pas orice termen cu „oglinda” sa. Asupra termenilor care devin zero nu se vor mai efectua alte operații. După efectuarea celorKtransformări, să se determine cea mai lungă secvență de numere care au cifra1pe aceeași poziție în reprezentarea lor în baza doi. Dacă sunt mai multe astfel de secvențe având lungimea maximă, se va afișa cea mai din stânga.
ONI 2017, Clasa a IX-a
- Fișiere
- concurs
- Clasa 9 Probleme diverse Probleme diverse