Lista de probleme 63
Filtrare
#875
Stiva
Să se scrie un program care gestionează o stivă de numere întregi. Inițial stiva este vidă. Programul va citi de la tastatură o listă de operații, care pot fi:
push X– adaugă valoarea întreagăXpe stivă;pop– elimină elementul din vârful stivei;top– afișează elementul din vârful stivei.
Programul va realiza asupra stivei operațiile citite, în ordine. Afișările se fac pe ecran, câte o valoare pe linie.
- Consola
- Silviu Candale
- ușoară
- Clasa 10 Structuri de date liniare Stiva
#877
Cuburi2
Gigel are un set de n cuburi. Fiecare cub este marcat cu un număr natural, de la 1 la n și i se cunoaște lungimea laturii – număr natural. Cu o parte dintre aceste cuburi Gigel va construi o stivă, astfel:
- fiecare cub se analizează o singură dată, în ordinea numerelor marcate;
- dacă stiva nu conține niciun cub, cubul curent devine baza stivei
- dacă cubul curent are latura mai mică sau egală cu cubul din vârful stive, se adaugă pe stivă;
- dacă cubul curent are latura mai mare decât cubul din vârful stivei, se vor înlătura de pe stivă cuburi (eventual toate) până când cubul curent are latura mai mică sau egală cu cubul din vârful stivei.
Să se afișeze numerele de pe cuburile existente la final în stivă, de la bază spre vârf.
- Consola
- Silviu Candale
- ușoară
- Clasa 10 Structuri de date liniare Stiva
#2650
books
Eroul nostru, Căldărușe, are un număr n de cărți pe care le are aranjate una peste cealaltă (sub forma unui stack). Cartea din vârf are valoarea \( {a}_{1} \), următoarea \( {a}_{2} \) și așa mai departe. Cartea de la bază are indicele n (\( {a}_{n} \)). Toate numerele sunt distincte. Căldărușe vrea să mute toate cărțile în ghiozdanul lui în exact n pași. În timpul pasului de ordin i, el vrea să mute cartea cu numărul \( {b}_{i} \) în ghiozdan. Dacă această carte se află în stack, el o ia atât pe ea, cât și toate cărțile situate deasupra acesteia și le pune în ghiozdan; în caz contrar, el nu va face nimic și va trece la următorul pas. Ajutați-l pe Căldărușe! Spuneți-i voi numărul de cărți pe care le va pune în ghiozdan în timpul fiecărui pas.
- Consola
- Vintilă Valentin
- medie
- Clasa 10 Structuri de date liniare Stiva
- CNCV
- Stiva
#878
Intervale4
Se consideră un șir de n intervale închise întregi. Două intervale consecutive în șir care au intersecția nevidă se reunesc și se înlocuiesc în șir cu intervalul reuniune. Operația se repetă până când nu mai sunt în șir două intervale consecutive cu intersecția nevidă.
Să se determine câte intervale există în șir după realizarea acestor operații.
- Fișiere
- Silviu Candale
- medie
- Clasa 10 Structuri de date liniare Stiva
#870
Depou
Se consideră un depou de cale ferată precum cel din imagine:
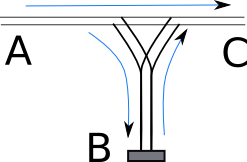
Pe linia A se află n vagoane, numerotate cu valori distincte de la 1 la n, într-o ordine oarecare. Vagoanele trebuie mutate pe linia C, în ordinea 1 2 .. n. Pentru aceasta se poate muta câte un vagon de pe o linie pe alta, în ordinea indicată de săgeți:
A -> B, A -> C sau B -> C.
Să se determine o succesiune de operații care să mute toate vagoanele de pe linia A pe linia C în ordinea dorită.
- Consola
- Silviu Candale
- medie
- Clasa 10 Structuri de date liniare Stiva
#848
Paranteze1
Se dau n șiruri de paranteze rotunde. Să se stabilească, despre fiecare șir, dacă este corect parantezat.
- Fișiere
- ușoară
- Clasa 10 Structuri de date liniare Stiva
#3795
Paranteze4
Să se scrie un program care citește un șir de paranteze rotunde care se închid corect (corect parantezat) în care parantezele deschise sunt numerotate de la stânga la dreapta, începând de la 1, și determină pentru fiecare paranteză închisă numărul de ordine al parantezei deschise corespunzătoare.
- Consola
- ușoară
- Clasa 10 Structuri de date liniare Stiva
#852
Paranteze3
Se dau n șiruri de paranteze rotunde sau pătrate. Să se stabilească, despre fiecare șir, dacă este corect parantezat.
- Fișiere
- ușoară
- Clasa 10 Structuri de date liniare Stiva
#849
Paranteze2
Se dă un șir de paranteze rotunde care se închid corect (corect parantezat). Să se determine adâncimea parantezării.
- Fișiere
- ușoară
- Clasa 10 Structuri de date liniare Stiva
#4263
ifelse
Studiind instrucțiunea if, Alinutza a aflat că ramura else se asociază celui mai apropiat if neasociat încă. Aprofundând studiul, a extras din fiecare program scris cuvintele if și else. Din neatenție a transcris greșit, pierzând asocierea corectă if else. Ajutați-o voi să aibă scrierea corectă, folosind un număr minim de modificări. O modificare înseamnă să înlocuim un cuvânt if cu else sau un cuvânt else cu if.
InfoCNFB 2022
- Fișiere
- Sofia Vitelaru
- medie
- Clasa 10 Structuri de date liniare Stiva