Lista de probleme 32

Se consideră două numerele naturale K și S și un șir de N numere naturale a[1], a[2],…, a[N]. O secvenţă de lungime K este un subşir format din K elemente aflate pe poziţii consecutive în şir: a[i], a[i+1],.., a[i+k-1]. Parcurgând șirul de la stânga la dreapta, începând cu primul element, se elimină prima secvență de lungime K, cu suma elementelor strict mai mare decât numărul S. În urma ștergerii șirul va avea N-K elemente: a[1], a[2],…, a[N-K]. Operația de ștergere continuă după aceleași reguli până când nu mai există secvențe care pot fi eliminate.

Să se scrie un program care citind numerele N, K, S și cele N elemente din șir rezolvă cerințele:
1) Determină numărul secvențelor care se vor elimina respectând condiția din enunț.
2) Considerând că în șirul citit nu sunt posibile eliminări de secvențe conform condiției din enunț, programul determină numărul de elemente a[i] din șir cu proprietatea următoare: ștergerea lui a[i] conduce la obținerea unui șir în care se mai poate elimina cel puțin o secvență de K elemente cu sumă strict mai mare ca S.

Se consideră un șir de N numere naturale, notate x 1, x 2, x 3,…, x N. Definim pentru orice pereche de indici i, j, 1 ≤ i ≤ j ≤ N, distanța între elementele x i și x j ca fiind egală cu j – i.

Acest șir va fi codificat după următoarele reguli:

• fiecare element din șir este înlocuit cu indicele celui mai apropiat element din șir (cel față de care distanța este minimă) strict mai mare decât el;
• dacă pentru un element din șir există două elemente care respectă regula de mai sus, atunci el va fi înlocuit cu indicele mai mare, adică al elementului strict mai mare decât el, aflat în dreapta lui;
• elementele de valoare maximă din șir vor fi înlocuite cu -1.

Scrieți un program care codifică un șir de N valori, după regulile descrise.

Considerăm un şir de numere a1, a2, …, aN. O secvenţă nevidă în acest şir este de forma ai, ai+1, …, aj, unde i ≤ j. De exemplu, pentru N=4 şi şirul 2 3 4 3, secvenţele nevide sunt: 2, 2 3, 2 3 4, 2 3 4 3, 3, 3 4, 3 4 3, 4, 4 3, 3. Definim puterea unui element ai ca fiind numărul de secvenţe care-l conţin pe ai şi în care ai este strict mai mare decât celelalte elemente ale fiecăreia dintre respectivele secvenţe. Astfel în şirul 2 3 4 3 puterea elementului a1 este 1 (fiind maxim doar în secvenţa formată din el însuşi), a elementului a2 este 2 (a2 fiind maxim în secvenţele 2 3 şi 3), a elementului a3 este 6 (fiind maxim în secvenţele 2 3 4, 2 3 4 3, 3 4, 3 4 3, 4 şi 4 3), iar a elementului a este 1.

Scrieţi un program care determină puterea cea mai mare a unui element din şirul dat, precum şi numărul de elemente din şir care au cea mai mare putere.

Se dă șir de N caractere, format din litere mici ale alfabetului englez, din care trebuie eliminate K secvențe disjuncte de lungime L. Care este cel mai mic şir din punct de vedere lexicografic ce se poate obține după eliminarea tuturor celor K secvențe.

Eroul nostru, Căldărușe, are un număr n de cărți pe care le are aranjate una peste cealaltă (sub forma unui stack). Cartea din vârf are valoarea \( {a}_{1} \), următoarea \( {a}_{2} \) și așa mai departe. Cartea de la bază are indicele n (\( {a}_{n} \)). Toate numerele sunt distincte. Căldărușe vrea să mute toate cărțile în ghiozdanul lui în exact n pași. În timpul pasului de ordin i, el vrea să mute cartea cu numărul \( {b}_{i} \) în ghiozdan. Dacă această carte se află în stack, el o ia atât pe ea, cât și toate cărțile situate deasupra acesteia și le pune în ghiozdan; în caz contrar, el nu va face nimic și va trece la următorul pas. Ajutați-l pe Căldărușe! Spuneți-i voi numărul de cărți pe care le va pune în ghiozdan în timpul fiecărui pas.

Se consideră un cuvânt format numai din litere mici și un număr natural nenul K. Să se determine cuvântul minim lexicografic obținut prin eliminarea a exact K litere din cuvântul inițial.

Pentru că e criză, cu ocazia campaniei electorale, în loc de găleți pline cu făină, zahăr și bilete la teatru primiți un șir a1, a2, …, an care reprezintă o permutare a mulțimii {1,2,...,n}. Pentru fiecare secvență nevidă a permutării costul ei este valoarea maximă din acea secvență. Să se calculeze suma totală a costurilor tuturor secvențelor.

Se dă un număr natural N si un șir v de N numere naturale. Sa se răspundă la Q întrebări de tipul:

• D y: Care este cea mai mică poziție x, unde x > y, pentru care v[x] < v[y]? Dacă nu există o astfel de poziție, răspunsul acestei întrebări va fi N + 1.
• S y: Care este cea mai mare poziție x, unde x < y, pentru care v[x] < v[y]? Dacă nu există o astfel de poziție, răspunsul acestei întrebări va fi 0.

Se dă o stivă inițial vidă. Să se efectueze Q operații de forma:

1 x: Se adaugă x în stivă.
2: Se șterge elementul din vârful stivei.
3 S: Se întreabă dacă se poate scrie valoarea S ca sumă de elemente aflate în stivă. Fiecare element poate fi folosit o singură dată în calcularea sumei. Răspunsul va fi 1 în caz afirmativ și 0 în caz negativ.

Uitându-ne din New Jersey către New York, Manhattan, departe, în zare, se văd zgârie norii. De la distanță, nu distingem clădirile, ci numai o linie formată din segmente orizontale și verticale, așa numita skyline.

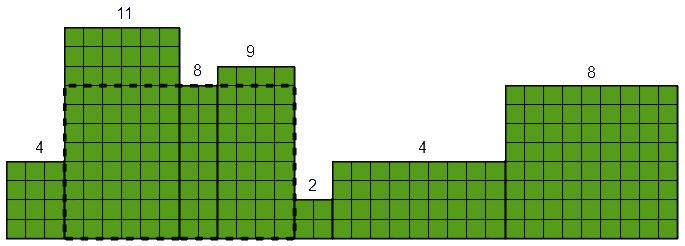
Determinați care este aria celui mai mare dreptunghi care se poate înscrie în skyline.