Lista de probleme 208

Toată lumea ştie că Fibocel este pasionat de numere şi că vrea să iasă în evidenţă cu orice preţ. Într-o zi, el s-a decis să numească un număr fibocel (după numele lui) dacă numărul de biţi egali cu 1 din reprezentarea binară a numărului este un număr Fibonacci.

Cum asta nu e de ajuns pentru el, Fibocel s-a decis să propună şi o problemă la concursul lui preferat de la Iaşi.

Să se raspundă la Q întrebări de forma: Câte numere fibocel există în intervalul închis [A, B]?

În seara dinaintea probei de concurs, Cobby a avut un vis demn de un Oscar, cu mai multe evenimente. Se făcea că lumea era reprezentată ca o matrice pătratică de latură N, cu liniile și coloanele numerotate de la 1 la N, în care fiecare element era inițial vid. Privind în jur, a realizat că atunci când visează un element al matricei, situat la intersecția liniei i cu coloana j, interiorul acestuia se împarte în N linii și N coloane, ca o nouă matrice. Apoi, dacă visează la un element din matricea nou formată sau
din cea inițială, se întâmplă la fel.

Pentru a nu se rătăci, eroul nopții a decis să atribuie un indice fiecărei matrice formată începând cu cea inițială căreia i-a asociat indicele 1. Matricele care se creează primesc indici numere naturale consecutive (2, 3, …), în ordinea în care se obţin. Astfel, fiecare element din visul lui Cobby este definit de 3 numere: id – indicele atribuit matricei din care face parte, i şi j – indicii liniei şi coloanei pe care se află elementul.

Cobby realizează că, oricât ar încerca, nu poate visa un element decât o singură dată. Pentru a face visul şi mai interesant, el reţine pentru fiecare matrice un număr natural denumit “coeficient de importanţă”, iniţial 0 pentru fiecare matrice din vis. Din când în când, eroul nostru alege una dintre matrice şi adaugă o valoare VAL la coeficientul de importanță al ultimelor NR matrice din care s-a obținut aceasta, inclusiv ea.

După ce au loc toate evenimentele din vis, Cobby vrea să ştie valoarea finală a coeficientului de importanţă pentru un șir de K matrice date prin indicii lor. Deoarece el se grăbeşte să participe la Concursul Naţional Urmaşii lui Moisil, îţi revine ţie misiunea de a găsi răspunsul pentru fiecare matrice.

Se dau N puncte în spațiul 3D prin coordonatele lor. Dorim să amplasăm două cuburi cu laturile paralele cu axele de coordonate, astfel încât fiecare punct să se afle pe una dintre feţele sau în interiorul a cel puțin unuia dintre cuburi. În plus, latura cubului de latură maximă dintre cele două trebuie să fie minimă.

Scrieţi un program care să determine latura cubului de latură maximă pentru două cuburi care realizează acoperirea mulțimii de puncte în condiţiile de mai sus.

La ora de geometrie, Aurel a primit de la profesorul X o temă foarte dificilă: fiind date N segmente orizontale (paralele cu axa Ox), cu extremităţile de coordonate numere naturale, să se numere câte dreptunghiuri speciale pot fi formate în plan, luând în considerare aceste segmente.

Un dreptunghi este special dacă respectă simultan următoarele trei condiţii:
1. Cele patru vârfuri ale dreptunghiului au coordonate numere naturale
2. Laturile dreptunghiului sunt paralele cu axa Ox, respectiv Oy
3. Fiecare dintre cele patru vârfuri ale dreptunghiului aparţine cel puţin unui segment

Scrieţi un program care să-l ajute pe Aurel să determine numărul de posibilităţi de a plasa un dreptunghi în plan astfel încât să fie dreptunghi special. Deoarece rezultatul poate fi foarte mare, se va determina numărul modulo 946021 (restul împărţirii numărului calculat la 946021).

Fiind date n numere naturale a1 , a2 ... an , se calculează ai ^ aj , pentru oricare i şi j (1 ≤ i < j ≤ n) şi se obţine un şir de valori naturale. Cu caracterul ^ s-a notat operatorul sau exclusiv pe biți (xor) şi se aplică conform regulii din tabelul de mai jos.

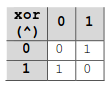
Fiind date cele n valori şi un număr natural nenul m, 1 ≤ m ≤ n*(n-1)/2, să se determine al m-lea număr din şirul obținut mai sus, considerând valorile în ordine crescătoare.

Se dă o permutare P a mulțimii {1,2, … ,N}. Se mai dau Q întrebări specificate prin câte un număr D.

Dacă D este pozitiv trebuie să determinăm a D-a permutare care succede lexicografic P iar dacă D este negativ, a D-a permutare care precede lexicografic P.

În Bistriţa sunt N copii, fiecare dintre ei având un număr preferat Xi . Copii se aşează pe un rând, cu poziţiile numerotate de la 1 la N. După ce copii s-au aşezat, profesoara de educaţie fizică le cere să execute M mişcări de tipul (a, b), cu semnificaţia că îşi vor schimba ordinea copiii care se află între poziţiile a şi b, inclusiv.

Să se răspundă la Q întrebări de tipul p, cu semnificaţia: care este numărul preferat al copilului, care se află pe poziţia p, după executarea mişcărilor cerute de profesoara de educaţie fizică.

Fie \(z \in R, z \neq 0\) astfel încât \(z + \frac{1}{z} = k, k \in N\).

Dându-se k și un număr natural n, se cere:

a) să calculați \(z^2 + \frac{1}{z^2}\) ;
b) să se determine \(z^n + \frac{1}{z^n}\) .

Marele inginer NN, expert în construirea de baraje, a primit de data aceasta o sarcină mai îmbârligată. Acesta are de construit M baraje peste mai multe râuri dintr-o deltă și îşi planifică pe hârtie milimetrică construcţia fiecărui baraj în parte.

Toate râurile peste care are de construit baraje sunt braţe ale aceluiaşi fluviu şi toate pornesc din exact acelaşi punct pe lungimea fluviului. Pentru a-şi explica schiţa, NN marchează locul de despărţire a tuturor braţelor fluviului printr-un punct O, numit origine. Apoi, din origine pornesc N semidrepte, fiecare reprezentând o porţiune de uscat, astfel încât spaţiul gol dintre 2 semidrepte consecutive va fi considerat un braţ al fluviului.

După ce a desenat schiţa proiectului, NN se întreabă care e numărul de râuri pe care le acoperă complet fiecare baraj. Un baraj acoperă complet un râu dacă intersectează fiecare dintre malurile acestuia. Sarcina voastră este să îl ajutaţi oferindu-i informaţii precise pentru a-şi putea realiza planul cât mai eficient, păstrându-şi renumele.

Ferma lui Algo arată ca o gospodărie mare, în care îşi găsesc locul multe animale şi sunt cultivate pe suprafeţe întinse legume, cereale şi pomi fructiferi. În acest an, pomii a fost atacaţi de o musculiţă care le distruge fructele. Algo a căutat o soluţie pentru îndepărtarea musculiţelor, dar nu a găsit una eficientă. A observat însă că musculiţele sunt sensibile la fum. Aşa că a construit un dispozitiv alcătuit din două ţevi, cu care poate să tragă în acelaşi timp, pe aceeaşi direcţie, dar în sens invers, două baloane speciale umplute cu fum. La fiecare acţionare a dispozitivului sunt lansate cu aceeaşi viteză cele două baloane, care se sparg şi împrăştie fumul la contactul cu copacul.

Deoarece baloanele speciale şi tehnologia lui de a le umple cu fum sunt costisitoare, Algo îşi propune să alunge dăunătorii folosind cât mai eficient resursele. Astfel el vrea să folosească cât mai puţine baloane şi caută posibilitatea de a amplasa dispozitivul într-un punct din fermă care să îi permită trageri eficiente, adică să poată trage în toți pomii din fermă și la fiecare tragere să atingă doi pomi în acelaşi timp.

Determinaţi dacă este posibil să găsească acest punct.