Arbori binari de căutare

Definiție

Definiție: Se numește arbore binar de cautare un arbore binar în care fiecare nod are o cheie unică de identificare care respectă următoarele condiții:

• pentru orice subarbore, cheile nodurilor din subarborele stâng sunt mai mici decât cheia rădăcinii;
• pentru orice subarbore, cheile nodurilor din subarborele drept sunt mai mari decât cheia rădăcinii.

Exemplu

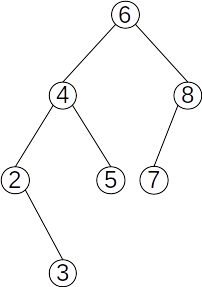
Observații:

• Conform definiției, cheile asociate nodurilor dintr-un arbore binar de căutare nu se pot repeta. Dacă se dorește repetarea lor, definiția trebuie modificată încât în subarborele drept (sau stâng) cheile să poată fi și egale cu cheia rădăcinii.
• În practică informația utilă din nodurile arborelui poate fi de orice tip, cu condiția să conțină și cheia. Pentru simplitate, în cele ce urmează informatia utilă va consta exclusiv în cheia de identificare.
• În cele ce urmează vom folosi reprezentarea dinamică a arborilor binari, prin referințe descendente. Structura C++ folosită pentru nodurile arborelui este cea uzuală:
  

  struct nod{
  	int info;
      nod * st, * dr;
  
  };
  
  

Proprietăți

• Parcurgerea în inordine a nodurilor unui arbore binar de căutare se face în ordinea crescătoare a cheilor.
• Operațiile uzuale cu un arbore binar de căutare sunt:
  • inserarea unui nod nou
  • căutarea unui nod
  • ștergerea unui nod
  • parcurgerea nodurilor din arbore
• Căutarea unui nod care are o cheie precizată se realizează destul de repede, deoarece, dacă rădăcina nu corespunde cheii date, căutarea va continua doar în unul dintre subarbori – stâng sau drept, în funcție de relația dintre cheia dată și cheia corespunzătoare rădăcinii.

Operații cu arborii binari de căutare

Așa cum ma văzut mai sus, principalele operații sunt:

• inserarea unui nod nou;
• căutarea unei valori;
• ștergerea unui nod;
• parcurgerea nodurilor din arbore (traversarea arborelui).

În implementarea acestor operații vom folosi metoda divide-et-impera. Principiul este:

• prelucrăm rădăcina;
• parcurgem subarborele stâng și/sau subarborele drept.

Inserarea

Se cunoaște adresa rădăcinii unui arbore binar de căutare (sau NULL dacă arborele este vid) și o valoare. Se cere să se insereze în arbore un nod care are drept cheie de identificare valoarea dată.

Inserarea trebuie realizată astfel încât să se păstreze proprietatea specifică arborilor binari de căutare!

Procedăm astfel:

• dacă arborele este nevid:
  • dacă valoarea dată este identică cu cheia rădăcinii se renunță la inserare;
  • dacă valoarea dată este mai mică decât cheia rădăcinii, se continuă cu subarborele stâng;
  • dacă valoarea dată este mai mare decât cheia rădăcinii, se continuă cu subarborele drept;
• dacă arborele este vid:
  • se creează un nod nou care având cheia egală cu valoarea dată și descendenți stâng și drept NULL. Legarea nodului la subarbore se face automat, datorită transmiterii prin referință a parametrului care reprezintă adresa rădăcinii.

Pentru a creea un arbore binar de căutare vom porni de la un arbore vid și vom aplica în mod repetat operația de inserare.

Funcție C++

void Inserare(nod * & R, int x)
{
	if(R != NULL)
    {
    	if(R->info == x)
        	return;
        else
        	if(R->info > x)
            	Inserare(R->st , x);
            else
            	Inserare(R->dr , x);
    }
    else
    {
    	R = new nod;
        R->info = x;
        R->st = NULL;
        R->dr = NULL;
    }	
}

Căutarea

Se cunoaște adresa rădăcinii unui arbore binar de căutare (sau NULL dacă arborele este vid) și o valoare. Se cere să se stabilească dacă există în arbore un nod care are cheia de identificare egală cu valoarea dată.

Procedăm astfel:

• dacă arborele este nevid:
  • dacă valoarea dată este identică cu cheia rădăcinii atunci am găsit nodul căutat;
  • dacă valoarea dată este mai mică decât cheia rădăcinii, se continuă căutarea în subarborele stâng;
  • dacă valoarea dată este mai mare decât cheia rădăcinii, se continuă căutarea în subarborele drept;
• dacă arborele este vid:
  • valoarea căutată nu există în arbore.

Funcție C++

Funcția de mai jos caută valoarea x în arborele pentru care adresa rădăcinii este memorată în pointerul R. Funcția returnează adresa nodului care are cheia egală cu x sau NULL dacă nu există un asemenea nod.

nod * Cautare(nod * R , int x)
{
	if(R == NULL)
		return NULL;
	if(R->info == x)
		return R;
	if(R->info > x)
		return Cautare(R->st , x);
	else
		return Cautare(R->dr , x);
}

Ștergerea unui nod

Se cunoaște adresa rădăcinii unui arbore binar de căutare (sau NULL dacă arborele este vid) și o valoare. Se cere să se șteargă din arbore nodul care are cheia de identificare egală cu valoarea dată.

Ștergerea trebuie realizată astfel încât să se păstreze proprietatea specifică arborilor binari de căutare!

Procedăm astfel:

• dacă arborele este nevid:
  • dacă valoarea dată este identică cu cheia rădăcinii atunci am găsit nodul căutat. Procedăm astfel:
    • dacă nodul este terminal (subarborele stâng și subarborele drept sunt vizi) se va șterge acest nod, iar adresa reținută de părinte pentru el devine NULL;
    • dacă numai subarborele stâng este nevid nodul se va șterge, iar adresa reținută de părinte pentru el devine adresa subarborelui stâng;
    • dacă numai subarborele drept este nevid nodul se va șterge, iar adresa reținută de părinte pentru el devine adresa subarborelui drept;
    • dacă ambii subarbori sunt nevizi:
      • se identifică cel mai mare nod din subarborele stâng (cel mai din dreapta nod al subarborelui stâng). Acest nod nu poate avea subarbore drept!
      • se copiază informația din acest nod în nodul analizat;
      • nodul identificat este șters. Ștergerea se realizează ca în cazul în care nodul este terminal sau ca în cazul în care nodul are numai subarbore stâng;
  • dacă valoarea dată este mai mică decât cheia rădăcinii, se continuă căutarea în subarborele stâng;
  • dacă valoarea dată este mai mare decât cheia rădăcinii, se continuă căutarea în subarborele drept;
• dacă arborele este vid:
  • valoarea căutată nu există în arbore.

Secvența C++

Mai jos sunt prezentate două funcții: Stergere și StAux. Funcția StAux tratează cazul când nodul curent trebuie șters și are ambii subarbori.

void StergAux(nod * & p, nod * & R)
{
	// R - nodul care trebuie sters
	// p - pointer cu care identificăm nodul cel mai din dreapta
	if(p->dr)
		StergAux(p -> dr , R);
	else
	{
		R->info = p->info;
		nod * aux = p;
		p = p->st;
		delete aux;
	}
}

void Stergere(nod * & R , int x)
{
	if(R != NULL)
	{
		if(R->info == x)
		{
			// nodul trebuie șters
			if(R->st == NULL && R->dr == NULL)
			{
				delete R;
				R = NULL;
			}
			else
				if(R->dr == NULL)
				{
					nod * aux = R;
					R = R->st;
					delete aux;
				}
				else
					if(R->st == NULL)
					{
						nod * aux = R;
						R = R->dr;
						delete aux;
					}
					else
						StergAux(R->st, R);
		}
		else
			if(R->info > x)
				Stergere(R->st , x);
			else
				Stergere(R->dr , x);
	}
	else
		return; // valoarea x nu apare în arbore
}

Parcurgerea

Arborii binari de căutare pot fi parcurși în orice mod: inordine, preordine, postordine. Datorită structurii interne a arborilor (pentru orice subarbore, cheia asociată rădăcinii este mai mare decât orice cheie din subarborele stâng și mai mică decât orice cheie din subarborele drept), parcurgerea în inordine (Stâng-Rădăcină-Drept)se face în ordinea crescătoare a cheilor!

Pentru a realiza o parcurgere în ordinea descrescătoare a cheilor, folosim tot o parcurgere în inordine, dar de tip Drept-Rădăcină-Stâng!

Secvență C++

void Afisare(nod * r)
{
    if(r != NULL)
    {
		Afisare(r->st);
		cout << r->info << " ";
		Afisare(r->dr);
	}
}

Concluzii

• Căutarea rapidă a informațiilor este foarte importantă în practică, arborii binari de căutare fiind utilizați ca suport pentru diverse structuri de date eficiente.
• Eficiența operațiilor depinde de ordinea în care se realizează inserarea nodurilor în arbore. De exemplu, dacă nodurile sunt create în ordinea crescătoare a cheilor, arborele devine degenerat, fiecare nod având numai descendent drept. Operațiile nu mai sunt eficiente, complexitatea lor devenind \(O(n)\), unde \(n\) este numărul nodurilor din arbore.
• Pentru a evita această situație, arborii binari de căutare primesc proprietăți suplimentare astfel încât să devină arbori echilibrați – să aibă înălțimea mică în raport cu numărul \(n\) de noduri: aproximativ \(\log_2n\).
  • operațiile de inserare, ștergere și căutare aplicate pe arborii binari de căutare echilibrați au complexitatea \(O(\log n)\);
  • exemple de arbori echilibrați: arborii AVL (Adelson-Velskii și Landis au fost doi cercetători sovietici care au folosit prima dată arborii echilibrați), arborii roșu-negru.
• Containerele STL map și set sunt implementate cu ajutorul arborilor binari de căutare echilibrați – de regulă arbori roșu-negru.