Lista de probleme 2
Nivelul concursului: Județean
http://olimpiada.info/oji2016/
Grupe
Clasa a V-a Clasa a VI-a Clasa VII-a Clasa VIII-a Clasa a IX-a Clasa a X-a Clasele XI-XII
#1622
Elicoptere
Arhipelagul Zopopan este format din n insule de formă triunghiulară numerotate de la 1 la n. Fiecare insulă este localizată prin coordonatele carteziene ale vârfurilor.
Administrația dorește să cumpere elicoptere pentru a realiza transportul între insule. Un elicopter va putea să asigure o rută între două insule pe distanța minimă obținută pe orizontală sau verticală (paralel cu axele de coordonate). În plus, datorită capacității rezervorului o astfel de rută nu poate să depășească o valoare k – număr natural. Elicopterele parcurg rutele în ambele sensuri.
Investiția trebuie să îndeplinească următoarele condiții:
- Numărul de elicoptere cumpărate să fie minim.
- Numărul de perechi de insule între care se poate realiza transportul, folosind unul sau mai multe elicoptere să fie maxim.
- Suma lungimii tuturor rutelor să fie minimă.
Să se scrie un program care pentru n, k şi coordonatele vârfurilor insulelor cunoscute, determină:
- numărul minim de elicoptere ce vor fi cumpărate de administraţie;
- numărul perechilor neordonate de insule între care se poate realiza transportul prin elicoptere direct sau indirect;
- suma distantelor parcurse de toate elicopterele cumpărate (distanța parcursă de un elicopter se consideră distanța dintre insulele între care acesta asigură transportul).
OJI 2016, Clasele XI-XII
- Fișiere
- Doru Popescu Anastasiu
- concurs
- Clasa 11 Teoria Grafurilor Parcurgerea grafurilor neorientate
- Algoritmul lui Kruskal
- Geometrie
#1623
SumMax1
Avem o matrice triunghiulară cu n linii, cu elemente numere întregi. În această matrice putem construi un traseu după următoarea regulă:
- primul element al traseului este elementul
a1,1 - dacă elementul
ai,japarţine traseului, atunci următorul element al traseului poate fi doarai+1,jsauai+1,j+1, pentru orice1≤j≤i<n. - traseul se va codifica cu numerele de ordine ale coloanelor, parcurgând liniile de la
1lan. Valoarea traseului este egală cu suma elementelor ce îl formează.
Traseul evidenţiat în exemplul din dreapta are valoarea5+4+6+5+4=24, şi se codifică cu1,2,3,3,4.
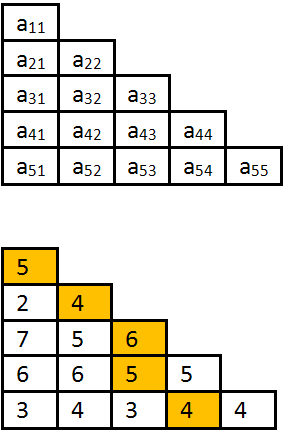
Fie mulţimea tuturor traseelor de valoare maximă generate în ordine lexicografică și numerotate. Pentru exemplul de mai sus avem șase trasee de lungime maximă:
- traseul 1.
1 1 1 1 2 (5+2+7+6+4=24) - traseul 2.
1 1 1 2 2 (5+2+7+6+4=24) - traseul 3.
1 2 2 2 2 (5+4+5+6+4=24) - traseul 4.
1 2 3 3 4 (5+4+6+5+4=24) - traseul 5.
1 2 3 4 4 (5+4+6+5+4=24) - traseul 6.
1 2 3 4 5 (5+4+6+5+4=24)
Cunoscând dimensiunea și elementele unei matrice triunghiulare, respectiv două numere naturale st şi dr (st≤dr), se cere să se determine:
- Numărul total al traseelor de valoare maximă. În cazul în care această valoare depășește
2000000000, se va tipări valoarea2000000001; - Traseele cu numerele de ordine
st,st+1, … ,dr.
OJI 2016, Clasele XI-XII
- Fișiere
- Zoltan Szabo
- concurs
- Clasa 11 Programare dinamică Probleme diverse de programare dinamică