Lista de probleme 14

Maria are în camera sa N mărgele așezate una lângă alta. Pe fiecare dintre ele este scris un număr natural format din cifre nenule distincte. Pentru fiecare mărgea, Maria șterge numărul și în locul său scrie altul, având doar două cifre, respectiv cifra minimă și cifra maximă din numărul scris inițial, în ordinea în care aceste cifre apăreau înainte de ștergere. Acum Maria consideră că mărgelele sunt de două tipuri, în funcție de numărul de două cifre scris pe ele: tipul 1 (cele care au cifra zecilor mai mică decât cifra unităților) și tipul 2 (celelalte). Folosind mărgelele, fetița dorește ca prin eliminarea unora dintre ele (dar fără să le schimbe ordinea celorlalte) să obțină un colier circular cât mai lung care să respecte proprietatea că oricare două mărgele vecine ale sale sunt de tipuri diferite. În colierul format cu mărgelele rămase după eliminare se consideră că prima mărgea este vecină cu ultima.

1) determinați numărul de mărgele de tipul 1;
2) determinați numărul maxim de mărgele pe care le poate avea colierul;

La întâlnirea anuală a cârtițelor, la concursul pentru selecția noilor membri ai consiliului director, a fost propusă următoarea problemă:

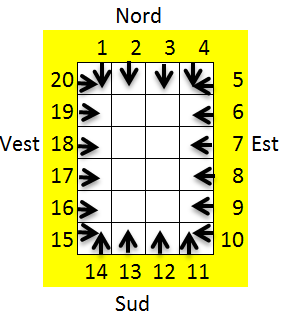De jur-împrejurul unui teren dreptunghiular împărțit în n*m celule de formă pătrată, cu aceeași arie, cârtițele au săpat galerii exterioare. Celulele aflate pe marginea terenului sunt numerotate consecutiv, de la 1 la 2*(n+m), începând din colțul din stânga-sus, ca în imaginea alăturată. În galeriile exterioare, pe marginea terenului, se află t cârtițe care sunt pregătite să sape galerii interioare. Cârtițele aflate pe latura de Nord a terenului se vor deplasa către Sud, cele care se află pe latura de la Est se vor deplasa către Vest, cele care se află pe latura de la Sud se vor deplasa către Nord, iar cele care se află pe latura de la Vest se vor deplasa către Est.

Cârtițele încep să sape în același timp. În fiecare oră, o cârtiță sapă într-o singură celulă a terenului.

O cârtiță se oprește dacă:

• ajunge într-o altă galerie interioară; ea nu sapă în aceasta, iar galeria ei se unește cu cea în care ajunge;
• în celula în care sapă, mai sapă și alte cârtițe, în aceeași oră; galeriile lor se unesc într-o singură galerie și toate aceste cârtițe se opresc;
• ajunge pe marginea terenului, în partea opusă celei din care a plecat, galeria săpată de ea până în acest moment comunicând acum cu galeria exterioară, în care ea nu sapă.

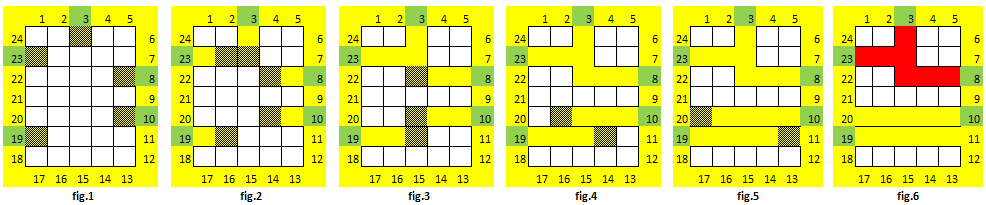
De exemplu, dacă pe marginea unui teren format din 7x5 celule, se află 5 cârtițe, în celulele 3, 8, 10, 19 și 23, atunci, după o oră, terenul are configurația din fig.1, după două ore, configurația din fig.2, după trei ore, configurația din fig.3 (ultima cârtiță ajunge în galeria primei cârtițe și primele două cârtițe sapă în aceeași celulă și apoi se opresc), după 4 ore, configurația din fig.4, după 5 ore, configurația din fig.5, când cele două cârtițe rămase sapă pe marginea terenului și apoi se opresc pentru că au ajuns în galeria exterioară (fig.6). Galeriile acestora nu se unesc pentru că niciuna dintre ele nu a intrat în galeria celeilalte și nici nu s-au întâlnit într-o celulă.

Cunoscându-se numerele n, m, t și cele t celule exterioare în care se află cârtițele, să se determine:

1. numărul maxim de celule în care sapă o cârtiță până la oprirea tuturor cârtițelor;
2. numărul maxim de celule din care este formată o galerie interioară.

Alex s-a angajat în vacanța de vară ca barman. Pentru că îi place să transforme munca la bar într-un spectacol, uneori aranjează mai multe pahare identice ca formă și dimensiune, dar de capacități diferite, sub forma unei stive.

Un pahar din stivă, cu excepția celor de la bază, se sprijină pe exact două pahare din rândul de mai jos. Paharele sunt numerotate ca în imaginea de mai jos. Nivelurile din stivă sunt de asemenea numerotate, începând cu 1, de la vârf, adică paharul 1 se află pe nivelul 1, paharele 2 și 3 pe nivelul 2, paharele 4, 5 și 6 sunt pe nivelul 3, ș.a.m.d.

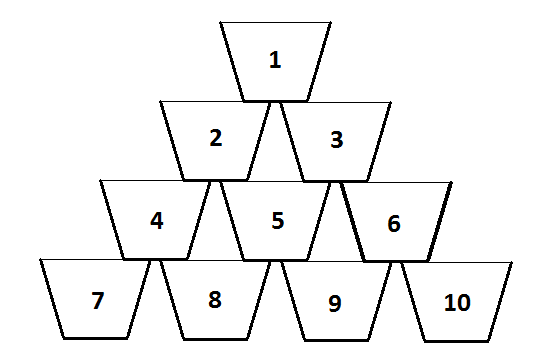
Alex toarnă în fiecare secundă câte un mililitru de apă (o picătură) în paharul numărul 1. Paharele au o proprietate ciudată atunci când sunt pline: primul mililitru care ajunge într-un pahar plin se va scurge instantaneu în paharul aflat imediat în stânga sa pe rândul de dedesubt, următorul mililitru se va scurge instantaneu în paharul aflat imediat în dreapta sa pe rândul de dedesubt și tot așa, alternativ câte o picătură în cele două pahare.

De exemplu când paharul 2 este plin, primul mililitru ce va ajunge în el se va scurge în paharul 4, următorul mililitru se scurge în paharul 5, al treilea mililitru se va scurge din nou în paharul 4, ș.a.m.d.

Atunci când într-un pahar plin aflat la baza stivei ajunge un nou mililitru de apă, acesta se scurge instantaneu pe masă.

Cunoscând numărul de pahare din rândul de la baza stivei și faptul că stiva este completă (toate rândurile conțin numărul maxim de pahare ce se pot așeza după regula de mai sus, iar pe cel mai de sus rând se găsește un singur pahar), să se scrie un program care determină:

1. Care este nivelul minim (cel mai de sus) care are suma capacităților tuturor paharelor de pe nivel maximă?
2. Care este numărul minim de secunde necesar pentru a umple toate paharele folosind procedeul descris mai sus și câți mililitri de apă se risipesc (se scurg pe masă) în acest caz?

Un copil dorește să găsească un mod original de a-și codifica numele și folosește în acest scop o figură formată doar din triunghiuri, desenată pe o foaie de hârtie. El plasează fiecare literă din numele său, în câte un triunghi. Dacă numele lui este DARIUS, atunci foaia de hârtie va arăta ca în figura 1. Pe primul rând așează prima literă, pe al doilea rând următoarele trei litere, pe al treilea rând următoarele cinci litere, și așa mai departe până când așează toate literele din nume. Dacă numele nu are suficiente litere, copilul folosește caracterul * pentru a completa ultimul rând pe care pe care a așezat litere. Nemulțumit că numele poate fi citit relativ ușor, răstoarnă figura, rotind foaia de hârtie, în sensul acelor de ceasornic, obținând astfel figura 2.

Cunoscând literele numelui, scrieți un program care determină și afișează în fișierul de ieșire:

1. Numărul de caractere * pe care trebuie să le utilizeze pentru a completa ultimul rând;
2. Prima literă de pe fiecare rând din figura inițială;
3. Șirul literelor de pe fiecare rând, după rotirea foii de hârtie.

Se consideră numerele naturale A (format din două sau trei cifre, toate distincte și nenule) și X (format din N cifre, toate nenule).

Din numărul X, folosind toate cele N cifre ale sale, se poate construi un cel mai mare număr natural Y strict mai mic decât X. De exemplu, pentru X=121621 se construiește Y=121612.

Tot din numărul X, se poate obține numărul A prin ștergerea unor cifre din scrierea lui X și alipirea celor rămase, fără a le schimba ordinea. De exemplu, dacă X=121621 și A=12, există Z=3 posibilități distincte prin care să obținem numărul A din X și anume: 1) 121621; 2) 121621; 3) 121621.

Cunoscându-se numerele A, N și cele N cifre ale lui X, să se determine:

1. cel mai mare număr natural Y, strict mai mic decât X, care se poate obține rearanjând cifrele lui X;
2. numărul maxim Z de posibilități distincte prin care se poate obține numărul A din numărul X prin ștergerea unor cifre și alipirea celor rămase, fără a le schimba ordinea.

Elevii clasei pregătitoare se joacă la matematică cu numere. Învățătoarea are un săculeț plin cu jetoane, pe fiecare dintre ele fiind scrisă câte o cifră. Fiecare elev și-a ales din săculeț mai multe jetoane, cu care și-a format un număr. Pentru ca totul să fie mai interesant, elevii s-au grupat în perechi. Doamna învățătoare a oferit fiecărei perechi de elevi câte o cutiuță pentru ca cei doi să își pună împreună jetoanele. De exemplu, dacă unul din elevii unei echipe și-a ales jetoane cu care a format numărul 5137131 iar celălalt elev și-a ales jetoane cu care a format numărul 6551813, atunci cutiuța echipei va conţine 5 jetoane cu cifra 1, câte 3 jetoane cu cifra 3 şi 5 şi câte un jeton cu cifrele 6, 7 şi 8.

Doar Andrei stătea supărat pentru că numărul de elevi al clasei era impar iar el nu avea partener, motiv pentru care nu și-a mai ales jetoane. Din această cauză, doamna învățătoare i-a spus:

“- Alege o echipă din a cărei cutiuță poţi lua o parte din jetoane, dar ai grijă ca fiecare dintre cei doi elevi să-și mai poată forma numărul lui din jetoanele rămase, iar tu să poți forma un număr nenul cu jetoanele extrase!“.

Dar cum Andrei nu se mulţumea cu puţin, a vrut să aleagă acea echipă din a cărei cutiuță îşi poată forma un număr de valoare maximă folosind jetoanele extrase.

Scrieţi un program care să citească numărul N de cutiuțe și numerele formate de elevii fiecărei perechi și care să determine:

1) Numărul de cutiuțe din care Andrei poate lua jetoane respectând condiția pusă de doamna învățătoare;
2) Care este cel mai mare număr nenul pe care îl poate forma Andrei respectând aceeași condiție.

Un număr se numește palindrom dacă prima lui cifră este egală cu ultima, a doua cu penultima și așa mai departe. De exemplu numerele 1221, 505 și 7 sunt palindromuri, în vreme ce 500, 1410 și 2424 nu sunt palindromuri.

Similar, un număr se numește aproape palindrom dacă are aceleași perechi de cifre identice ca un palindrom, mai puțin o pereche în care cifrele diferă. De exemplu numerele 500, 1411, 2444, 1220, 53625, 14 și 4014 sunt numere aproape palindromuri, în vreme ce 1221, 1410, 6, 505, 22 și 512125 nu sunt numere aproape palindromuri deoarece fie sunt palindromuri, fie au prea multe perechi de cifre diferite.

Mai definim palindromul asociat al unui număr x ca fiind cel mai mic număr palindrom p strict mai mare decât x (p>x). De exemplu palindromul asociat al lui 5442 este 5445, palindromul asociat al lui 2445 este 2552, al lui 545 este 555, al lui 39995 este 40004, al lui 500 este 505, iar al lui 512125 este 512215.

Scrieţi un program care citind un număr natural nenul n și apoi un șir de n numere naturale determină:

1. câte dintre cele n numere sunt palindrom
2. câte dintre cele n numere sunt aproape palindrom
3. palindromurile asociate pentru cele n numere citite.

În anul 2214 a izbucnit primul război interstelar. Pământul a fost atacat de către n civilizaţii extraterestre, pe care le vom numerota pentru simplicitate de la 1 la n.

Pentru a se apăra, pământenii au inventat o armă specială ce poate fi încărcată cu proiectile de diferite greutăţi, fabricate dintr-un material special denumit narun. Dacă arma este programată la nivelul p, atunci un proiectil de greutate k va ajunge exact la distanţa kp km (k la puterea p) faţă de Pământ şi dacă în acel punct se află cartierul general al unui atacator, acesta va fi distrus. De exemplu, dacă arma este programată la nivelul 2, un proiectil de greutate 10 va distruge cartierul general al extratereştrilor situat la distanţa 102 = 100 km de Pământ.

Arma poate fi încărcată cu proiectile de diferite greutăţi, dar cum narunul este un material foarte rar şi foarte scump, pământenii vor să folosească proiectile cât mai uşoare pentru a distruge cartierele generale inamice.

Cunoscându-se n, numărul atacatorilor, precum şi cele n distanţe până la cartierele generale ale acestora, să se scrie un program care determină:

• cantitatea minimă de narun necesară pentru a distruge toate cartierele generale inamice;
• nivelurile la care trebuie programată arma, pentru a distruge fiecare cartier general inamic cu o cantitate minimă de narun.

Ana şi Bogdan au inventat din nou un joc, pe care l-au denumit ks. Pe tabla de joc sunt plasate pe poziţii consecutive n jetoane, pe fiecare jeton fiind scris un număr natural nenul.

Ana este prima la mutare şi are voie să extragă de pe tablă exact k jetoane situate pe poziţii consecutive.

Bogdan mută al doilea şi are şi el voie să extragă exact k jetoane, dintre cele rămase pe tablă, situate de asemenea pe poziţii consecutive.

Punctajul asociat unei mutări este egal cu suma numerelor scrise pe jetoanele extrase la mutarea respectivă.

Scopul Anei este să efectueze mutarea sa astfel încât punctajul obţinut de Bogdan să fie cât mai mic. Considerăm că atât Ana, cât şi Bogdan joacă optim.

Cunoscând numărul de jetoane de pe tabla de joc, valorile înscrise pe acestea, precum şi valoarea k, scrieţi un program care să determine care este cel mai bun punctaj pe care Bogdan îl poate obţine, ştiind că ambii jucători joacă optim.

Un indicator numeric este un dispozitiv de afişaj electronic destinat afişării unei cifre zecimale.
Acesta conține 7 segmente notate cu a, b, c, d, e, f, g, ca în figura de mai jos.

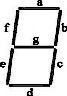
Afişarea unei cifre se face prin aprinderea unei combinații de segmente conform tabelului:

Cunoscând un număr natural N afișat cu ajutorul mai multor indicatoare numerice, să se scrie un program care determină:

1. Numărul de segmente aprinse pentru afișarea numărului N.
2. Numărul de numere distincte mai mari decât N,ce se pot forma prin aprinderea a cel puțin unui segment în plus, față de cele utilizate pentru afișarea numărului N, fără a folosi alte indicatoare numerice, și fără a stinge niciun segment dintre cele deja aprinse.