Lista de probleme 6
#1713
ecuatie3
Fie N și T două numere naturale.
Să se determine numărul soluțiilor diferite S, ale ecuației \( x_1 \cdot x_2 \cdot \cdots \cdot x_N = T \), în mulțimea numerelor naturale.
Lot Juniori Focsani, 2016
- Fișiere
- Ciprian Chesca
- concurs
- Clasa 10 Probleme diverse Combinatorică
#1714
Pandora
Anul 2154, undeva pe luxurianta planetă Pandora.
Aici coloniștii RDA (Resources Development Administration) doresc să-și stabilească o bază stelară pentru a exploata rezervele naturale de unobtainium, un minereu rar și prețios aflat din belșug pe munții plutitori (Hallelujah Mountains), munți ce plutesc lent purtați de curenții magnetici asemănător aisbergurilor în mare, pe suprafața planetei formată din gaz lichid.
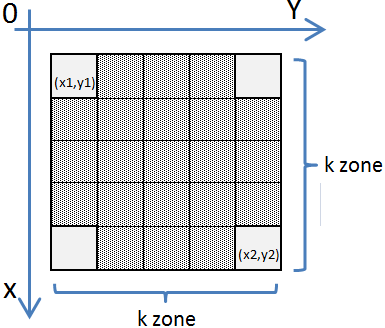
Pentru prospectarea și exploatarea zăcămintelor de minereu este necesară cartografierea suprafeței planetei și întocmirea unei hărți digitizate reprezentate sub forma unui tablou bidimensional. Astfel, regiunea de interes geologic este împărţită în N×N pătrate teritoriale identice (zone), fiecare zonă fiind identificată prin tripletul (x,y,c), unde (x,y) reprezintă coordonatele zonei teritoriale (x – linia, y – coloana), iar c cota (înălțimea). Între zonele ocupate de munții există vaste zone de gaz lichid, zone care au cota 0.
 Pentru recoltarea și transportul unobtainiumului către baza stelară coloniștii RDA folosesc spice-harvesters, nave speciale cu aterizarea pe verticală.
Pentru recoltarea și transportul unobtainiumului către baza stelară coloniștii RDA folosesc spice-harvesters, nave speciale cu aterizarea pe verticală.
Aterizarea pe munții plutitori reprezintă o adevărată provocare pentru piloții RDA. Pentru a putea ateriza, piloții trebuie să identifice un sector plat (platformă de aterizare), platformă care să respecte designul trenului de aterizare al navelor (vezi figura alăturată). Platforma are forma unui pătrat de latură k ce este format din k*k zone teritoriale, astfel (k*k)-4 zone au aceeași cotă, iar cele 4 colțuri ale pătratului au cota strict mai mică decât restul zonelor pătratului.
Cunoscând descrierea a M zone teritoriale ce alcătuiesc munții plutitori să se determine coordonatele colțului stânga-sus al platformelor de aterizare pentru munții plutitori care permit aterizarea.
Lot Juniori Focsani, 2016
- Fișiere
- Eugen Nodea
- concurs
- Clasa 10 Probleme diverse Diverse
- Fill
#1715
Inversiuni
Ludwig are o permutare p=(p[1],p[2],...,p[N]) a mulțimii {1,2,..,N} și o masă pe care putea așeza numerele din permutare. Ludwig ia primul număr din permutare, adică p[1], și îl așează pe masă. Al doilea număr, p[2], îl pune fie în stânga lui p[1], fie în dreapta lui p[1]. La fiecare pas, dacă s-au așezat pe masă deja numerele p[1], p[2], …, p[i], atunci numărul p[i+1] este pus fie în stânga numerelor deja așezate, fie în dreapta lor.
Ajutați-l pe Ludwig să determine o modalitate de așezare a întregii permutări pe masă astfel încât în final să se obțină o nouă permutare care are un număr minim de inversiuni.
Lot Juniori Focsani, 2016
- Fișiere
- Dan Pracsiu
- concurs
- Clasa 11 Probleme diverse Probleme diverse
- Șmenul lui Batog (Square Root Decomposition)
- Arbori indexați binar
#1712
Centura
Pe șoseaua care duce spre intrarea în oraș se află n autovehicule, dintre care m
sunt autovehicule de gabarit redus, pe care le vom numi în continuare autoturisme, iar restul sunt de gabarit mare și le vom numi camioane. Orașul are o șosea ocolitoare, numită popular centură. Camioanele trebuie să ocolească orașul
trecând în mod obligatoriu pe drumul de centură. Autoturismele pot continua drumul pe șoseaua care intră în oraș sau pot ocoli orașul intrând pe șoseaua de centură. Pe centură, camioanele circulă cu viteză redusă îngreunând traficul.
De aceea s-a impus restricția R: nu vor fi admise pe drumul de centură coloane formate din mai mult decât k camioane consecutive.
Cunoscând n, k și distribuția autovehiculelor pe șosea, să se determine două numere naturale V și T, unde V reprezintă numărul de variante de dirijare a traficului astfel încât să fie respectată restricția R, iar T reprezintă numărul minim de autoturisme care trebuie să fie deviate pe drumul de centură pentru a se respecta aceeași restricție R.
Lot Juniori Focsani, 2016
- Fișiere
- Constantin Galatan
- concurs
- Clasa 11 Programare dinamică Probleme diverse de programare dinamică
#1716
KDS
Se consideră un șir de numere naturale a[1], a[2], …, a[n] așezate circular. Acest lucru înseamnă că a[1] are ca vecini numerele a[n] și a[2], iar a[n] are ca vecini pe a[n-1] și a[1]. Se consideră de asemenea un număr natural K.
Să se determine suma maximă care se poate obține din exact K secvențe nevide, disjuncte și ne-vecine.
Lot Juniori Focsani, 2016
- Fișiere
- Cosmin Piț-Rada, Ionel-Vasile Piț-Rada
- concurs
- Clasa 11 Programare dinamică Probleme diverse de programare dinamică
#1717
Triunghi4
În țara lui Oblio toate lucrurile sunt sub formă de triunghi. Chiar și fotografiile sunt sub formă de triunghi. Fotografiile sunt formate din pixeli, care evident, la rîndul lor sunt triunghiuri ca în figura de mai jos.
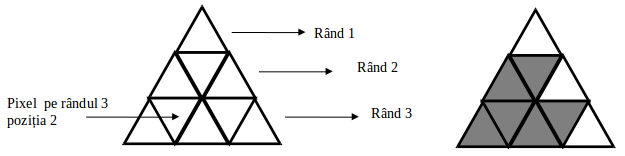
Fotografiile sunt alb negru și fiecare pixel este identificat prin rândul pe care se găsește și prin poziție, adică al câtelea triunghi este în rândul respectiv numărând de la 1, de la stânga la dreapta. Fiecare pixel are culoarea alb sau negru. Fiecare pixel are dimensiunea 1, dar mai mulți pixeli vecini pot forma triunghiuri cu vârful în sus cu laturi de diferite lungimi. În figura din dreapta avem 3 triunghiuri de dimensiune 1 (rândul 2 poziția 1, rândul 3 poziția 1, rândul 3 poziția 3) și un triunghi de dimensiune 2 (cu colțurile: în rândul 2 poziția 1, rândul 3 poziția 1 și rândul 3 poziția 3).
Se știe că în fotografie sunt n rânduri și m pixeli albi, fiecare pixel fiind identificat prin rând și poziție.
Se cere să se determine, pentru p lungimi de laturi date, câte triunghiuri de culoare neagră (adică pline numai cu pixeli de culoare neagră) și cu vârful în sus se găsesc în fotografie pentru fiecare lungime.
Lot Juniori Focsani, 2016
- Fișiere
- Octavian Dumitrascu
- concurs
- Clasa 11 Programare dinamică Probleme diverse de programare dinamică