Lista de probleme 7

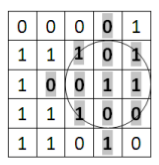Considerăm un caroiaj dreptunghiular cu L linii şi C coloane. Liniile sunt numerotate de la 1 la L de sus în jos şi coloanele de la 1 la C, de la stânga la dreapta. Caroiajul este împărţit în L*C pătrate cu latura egală cu două unităţi (2). În fiecare pătrat al caroiajului se găseşte una dintre valorile 0 sau 1. Se cunoaşte o poziţie (i, j) a unuia dintre pătratele caroiajului (1 ≤ i ≤ L, 1 ≤ j ≤ C).

Trebuie construit un cerc care să îndeplinească următoarele proprietăţi:

• Centrul cercului să coincidă cu centrul pătratului din poziţia (i, j);
• Raza cercului să fie un număr natural nenul;
• Diferenţa dintre numărul de valori 1 şi numărul de valori 0 aflate în pătratele acoperite de cerc să fie maximă.

Considerăm că un pătrat este acoperit de cerc dacă pătratul şi cercul au cel puţin un punct comun (aflat pe contur sau în interior). Dacă un pătrat este complet inclus în interiorul cercului se consideră că şi acel pătrat este acoperit de cerc (în figură, cercul desenat “acoperă” inclusiv pătratul din poziţia (3, 4) ). Cercul din figură are raza 3.

Determinaţi diferenţa maximă ce se poate obţine cu constrângerile de mai sus.

Banda piraţilor din Caraibe a pus la cale o nouă aventură! Căpitanul Jack se trezeşte prins într-o intrigă care îi va solicita din plin abilităţile şi inteligenţa. Deoarece el are o datorie de sânge faţă de legendarul Davey Jones, căpitanul corabiei fantomatice Olandezul Zburător, este
nevoit să-i cedeze acestuia o parte din ultima captură de diamante. Diamantele sunt depozitate în cufere şi trebuie să fie păzite foarte bine până în momentul în care Jack îşi va achita datoria.
El hotărăşte ca fiecare cufăr să fie păzit de câte doi piraţi şi pentru aceasta îşi organizează oamenii astfel:

• piraţi care vor forma rânduri;
• piraţi aşezaţi în formaţiuni circulare.

În ambele situaţii va fi aşezat câte un cufăr între oricare doi piraţi alăturaţi. În momentul în care corabia lui Davey Jones acostează la ţărm, acesta îi cere lui Jack să-şi plătească datoria astfel: „Alege N dintre piraţii tăi. Aceştia vor încărca pe corabie toate cuferele păzite doar de ei. Ai grijă ca numărul cuferelor să fie cel mai mare posibil! ”

Cunoscând numărul piraţilor şi modul lor de organizare în formaţiuni, scrieţi un program care să determine numărul maxim de cufere care pot fi încărcate pe corabie de cei N piraţi aleşi.

Gigel se lupta cu ardoare, în jocul primit în vacanţa de Paşti, cu fel şi fel de balauri. Într-una din zile a întâlnit un balaur care nu putea fi răpus cu nici una din armele obişnuite. Lur Ualab, căci aşa îl chema pe balaur, putea fi învins numai dacă cineva reuşea să îi rezolve ghicitoarea.

În fiecare luptă Lur Ualab îi dă lui Gigel un şir foarte lung format doar din litere mici ale alfabetului englez. Gigel trebuie să şteargă toate apariţiile, mai puţin una a fiecărei litere, astfel încât în şirul final obţinut să rămână toate literele distincte din şirul dat. La final, Gigel trebuie să îi dea lui Lur Ualab cel mai mic şir, din punct de vedere lexicografic, ce se poate obţine din şirul primit de el.

Scrieţi un program care să determine cel mai mic şir, din punct de vedere lexicografic, ce se poate obţine dintr-un şir dat, aplicând toate operaţiile de ştergere necesare.

Miriapodul Verone trăieşte cel mult 12 luni, dar nu este nefericit, întrucât viaţa i se pare lungă şi frumoasă. I se spune Verone deoarece corpul său cilindric este alcătuit din segmente colorate, iar fiecare segment poate avea doar una dintre culorile: verde, roşu sau negru.

În prima lună de viaţă, corpul miriapodului este format dintr-un singur segment. În fiecare dintre lunile următoare, fiecare segment s creşte în lungime şi se divide în trei segmente: s1, s2 şi s3. Segmentele s1 şi s3 păstrează culoarea segmentului s, în vreme ce segmentul s2, cel din mijloc, se colorează astfel: dacă s era verde, atunci s2 devine roşu. Dacă s era roşu, atunci s2 devine negru. Dacă s era negru, atunci s2 devine verde.

Cineva a găsit un fragment dintr-un asemenea miriapod, rezultat în urma unei lupte fatale pentru miriapod, cu o altă vieţuitoare.

Cunoscând culoarea unicului segment în prima lună de viaţă a miriapodului şi succesiunea de culori a fragmentului găsit, scrieţi un program care determină vârsta acestuia şi succesiunea de culori a tuturor segmentelor sale înainte de începerea luptei.

Pentru un şir de caractere S, vom nota cu lmax[S] lungimea maximă a unei secvenţe palindromice conţinută în şirul S. Astfel, pentru şirul S=”abAabaabC”, lmax[S]=4, iar pentru şirul S=”a”, lmax[S]=1.

Prin secvenţa palindromică a unui şir S înţelegem un subşir de caractere aflate pe poziţii consecutive, ce formează un palindrom.

Date fiind N şiruri de caractere S[1], S[2],…, S[n] şi o valoare naturală L, se cere să se determine numărul de secvenţe de şiruri de caractere de forma: S[i], S[i+1], … , S[j], cu i<=j, pentru care lmax[S[i]]+lmax[S[i+1]]+... +lmax[S[j]]=L.

Grădinarul Marian are la dispoziţie o permutare cu n elemente şi un număr natural S care iniţial are valoarea 0. Marian execută n operaţii de forma:

• alege elementul poziția x a minimului din permutare
• elimină acest element din permutare, iar toate elementele de la stânga sa le mută la sfârşitul permutării (păstrând ordinea elementelor din stânga)
• adună la S pe x.

Determinaţi valoarea lui S după ce grădinarul Marian termină de executat toate cele n operaţii.

Fie n un număr natural nenul, n > 1. Definim n(p) ca fiind descompunerea lui n în sumă de puteri naturale distincte ale numărului prim p.

Să se scrie un program care citeşte un număr natural n şi determină toate n(p) descompunerile numărului n.