Lista de probleme 2
Nivelul concursului: Județean
http://olimpiada.info/oji2017/
Grupe
Clasa a V-a Clasa a VI-a Clasa VII-a Clasa VIII-a Clasa a IX-a Clasa a X-a Clasele XI-XII
#2009
Accesibil
Un număr natural de cel puțin două cifre se numește accesibil dacă este format din cifre consecutive în ordine strict crescătoare. (23 și 6789 sunt numere accesibile, în timp ce 7, 2334 și 654 nu sunt numere accesibile)
Scrieți un program care să citească numerele k, n și un șir de n numere naturale și să afișeze:
a) cele mai mari 3 numere accesibile, nu neapărat distincte, din șirul de n numere;
b) câte dintre numerele din șirul dat care nu sunt accesibile, devin accesibile prin eliminarea exact a unei cifre;
c) cel mai mic și cel mai mare număr accesibil format din k cifre;
d) numărul numerelor accesibile pare de k cifre și numărul numerelor accesibile impare de k cifre.
OJI 2017, Clasa a VI-a
- Fișiere
- Ana Maria Arisanu
- concurs
- Clasa 9 Algoritmi elementari Cifrele unui număr
#2010
Fermier
Dorel și-a achiziționat o fermă cu n plantații și o mașină de transport cu o capacitate c, pentru transportul de îngrășăminte la toate plantațiile. Îngrășămintele se află într-un depozit, în cantitate suficientă pentru scopul propus. Plantațiile și depozitul sunt dispuse sub forma unui cerc. Există drumuri doar între plantația i și plantația i+1 (1≤i≤n-1), precum și între depozit și plantația 1 și depozit și plantația n, ca în figură.
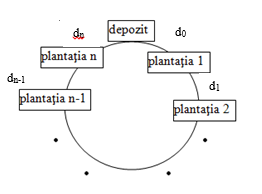
La o plantație i se poate ajunge de la depozit trecând prin plantațiile 1, 2,…, i-1 sau prin plantațiile n, n-1, …, i+1, alegerea făcându-se în funcție de traseul cel mai scurt. Se cunosc aceste distanțe, precum și cantitatea de îngrășăminte necesară pentru fiecare plantație. La fiecare încărcare, Dorel ia din depozit exact cantitatea c. Dorel vrea să-și organizeze bine munca la fermă și să consume cât mai puțină benzină prin alegerea celor mai scurte trasee de parcurs. Plantațiile trebuie să fie aprovizionate obligatoriu în ordinea următoare: mai întâi plantația 1, apoi plantația 2, plantația 3,…, plantația n. În plus, și-a propus să încarce o nouă cantitate de îngrășământ doar după ce a folosit toată cantitatea încărcată anterior. Transportarea îngrășămintelor pe plantații se face deci, începând cu plantația 1. După ce se transportă toată cantitatea necesară pentru această plantație, se trece la plantația 2, și tot așa în ordine la 3, 4 etc. până se deservește ultima plantație. Dacă după ce s-au transportat îngrășămintele necesare pentru plantația i în mașină au mai rămas încă îngrășăminte, acestea trebuie utilizate în continuare pentru alte plantații, alese în ordinea impusă (începând cu plantația i+1, apoi i+2 etc.), până se epuizează toată cantitatea transportată de mașină. Astfel, dacă de la plantația i trebuie să ajungă la plantația i+1, va alege cel mai scurt traseu dintre traseul direct de la plantația i la i+1 și traseul care trece prin plantațiile i-1, i-2, …, 1, depozit, n, n-1, …, i+1. La final, mașina trebuie să se întoarcă la depozit, goală sau cu cantitatea rămasă după aprovizionarea cu îngrășăminte a plantației n.
Ajutați-l pe Dorel să calculeze distanța parcursă pentru a transporta îngrășăminte la toate cele n plantații, conform cerințelor.
OJI 2017, Clasa a VI-a
- Fișiere
- Roxana Timplaru
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme diverse