Lista de probleme 208
Filtrare
#1236
Pastile
Manole este extrem de răcit. Din această cauză a mers la medicul de familie care l-a sfătuit urmeze un tratament cu N pastile, din care trebuie să ia în fiecare zi câte o jumătate. A cumpărat de la farmacie o cutie în care se aflau exact N pastile, fiecare dintre ele având pe suprafață o dungă care marchează jumătatea ei.
Manole începe să își ia tratamentul și constată că poate proceda doar astfel:
- scoate din cutie o pastilă întreagă din care folosește, în ziua respectivă, doar jumătate din ea, iar jumătatea rămasă o pune înapoi în cutie;
- scoate din cutie o jumătate de pastilă, rămasă din una din zilele anterioare, pe care o folosește în ziua respectivă.
Scrieți un program care determină numărul de posibilități în care poate lua toate cele N pastile, procedând după procedeul descris mai sus.
Lot Juniori, Valcea, 2015
- Fișiere
- Daniela Lica
- concurs
- Clasa 10 Probleme diverse Combinatorică
- Numarul lui Catalan
#1234
easydel
Victor are la dispoziție multe cuburi din lemn, toate de aceeași dimensiune, fiecare fiind colorat cu una din culorile 0, 1, 2, …, 9. El a inventat un joc sub forma unui algoritm:
- Pasul 0 – Se inițializează variabila
Xcu zero. - Pasul 1 – Se aleg la întâmplare un număr de cuburi și se formează cu ele un șir. Cuburile din șir sunt lipite unul de altul.
- Pasul 2 – Dacă toate cuburile din șir au aceeași culoare, atunci se afișează valoarea variabilei
Xși jocul se oprește. În caz contrar se trece la pasul3. - Pasul 3 – Se alege o culoare
Cși apoi toate cuburile de culoareaCse elimină din șir. Locurile cuburilor eliminate rămân temporar libere. - Pasul 4 – Orice cub din șir va fi deplasat spre stânga lui, cât timp pozițiile vecine sunt libere. Se mărește
Xcu1la fiecare deplasare cu o poziție. Operațiile de deplasare se încheie când nu se mai pot efectua mutări spre stânga. Apoi se revine la pasul2.
Se consideră un șir cu cel puțin două elemente reprezentând culorile cuburilor din șir. Se cere să se calculeze valoarea maximă pe care o poate avea X.
Lot Juniori, Valcea, 2015
- Fișiere
- concurs
- Clasa 10 Probleme diverse Diverse
#1246
Dispozitiv
Specificul insulelor din arhipelagul Maldive (Oceanul Indian) este faptul că toate cele N insule ale sale au forma unui triunghi. Localizarea acestor insule folosește coordonatele carteziene ale celor trei vârfuri.
Administrația acestor insule dorește să instaleze un dispozitiv de emisie-recepţie pe apă sau pe o insulă, într-un punct având coordonate numere naturale (xD, yD), ce transmite semnale numai pe direcții orizontale și verticale concomitent, cu următoarele proprietăţi:
- notând cu
NROnumărul de insule la care ajunge semnalul pe orizontală și cuNRVnumărul de insule la care ajunge semnalul pe verticală, sumaNRO + NRVtrebuie să fie maximă; - dacă există mai multe puncte cu proprietatea anterioară, atunci se va alege punctul cel mai mic în ordine lexicografică.
Să se scrie un program care cunoscând numărul de insule N şi coordonatele carteziene ale vârfurilor acestora, determină coordonatele xD și yD cu proprietățile din enunţ.
Lot Juniori Severin, 2015
- Fișiere
- Doru Popescu Anastasiu
- concurs
- Clasa 10 Probleme diverse Geometrie
#1713
ecuatie3
Fie N și T două numere naturale.
Să se determine numărul soluțiilor diferite S, ale ecuației \( x_1 \cdot x_2 \cdot \cdots \cdot x_N = T \), în mulțimea numerelor naturale.
Lot Juniori Focsani, 2016
- Fișiere
- Ciprian Chesca
- concurs
- Clasa 10 Probleme diverse Combinatorică
#1714
Pandora
Anul 2154, undeva pe luxurianta planetă Pandora.
Aici coloniștii RDA (Resources Development Administration) doresc să-și stabilească o bază stelară pentru a exploata rezervele naturale de unobtainium, un minereu rar și prețios aflat din belșug pe munții plutitori (Hallelujah Mountains), munți ce plutesc lent purtați de curenții magnetici asemănător aisbergurilor în mare, pe suprafața planetei formată din gaz lichid.
Pentru prospectarea și exploatarea zăcămintelor de minereu este necesară cartografierea suprafeței planetei și întocmirea unei hărți digitizate reprezentate sub forma unui tablou bidimensional. Astfel, regiunea de interes geologic este împărţită în N×N pătrate teritoriale identice (zone), fiecare zonă fiind identificată prin tripletul (x,y,c), unde (x,y) reprezintă coordonatele zonei teritoriale (x – linia, y – coloana), iar c cota (înălțimea). Între zonele ocupate de munții există vaste zone de gaz lichid, zone care au cota 0.
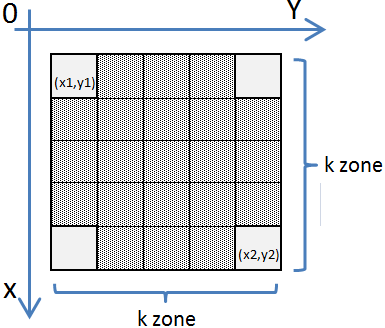 Pentru recoltarea și transportul unobtainiumului către baza stelară coloniștii RDA folosesc spice-harvesters, nave speciale cu aterizarea pe verticală.
Pentru recoltarea și transportul unobtainiumului către baza stelară coloniștii RDA folosesc spice-harvesters, nave speciale cu aterizarea pe verticală.
Aterizarea pe munții plutitori reprezintă o adevărată provocare pentru piloții RDA. Pentru a putea ateriza, piloții trebuie să identifice un sector plat (platformă de aterizare), platformă care să respecte designul trenului de aterizare al navelor (vezi figura alăturată). Platforma are forma unui pătrat de latură k ce este format din k*k zone teritoriale, astfel (k*k)-4 zone au aceeași cotă, iar cele 4 colțuri ale pătratului au cota strict mai mică decât restul zonelor pătratului.
Cunoscând descrierea a M zone teritoriale ce alcătuiesc munții plutitori să se determine coordonatele colțului stânga-sus al platformelor de aterizare pentru munții plutitori care permit aterizarea.
Lot Juniori Focsani, 2016
- Fișiere
- Eugen Nodea
- concurs
- Clasa 10 Probleme diverse Diverse
- Fill
#3930
Perioada1
Fie N un număr natural cu proprietatea că (N, 10) = 1.
Să se determine lungimea perioada T a fracţiei zecimale periodice simple \(\frac{1}{N}\)
Lot Juniori Magurele, 2016
- Fișiere
- Ciprian Chesca, Ionel-Vasile Pit-Rada
- concurs
- Clasa 10 Probleme diverse Diverse
- Indicatorul lui Euler
- Exponentiere rapida
#1914
Rica
Rică a învățat la școală despre șiruri recurente și a primit ca temă să lucreze cu un anumit șir. Rică știe că primele elemente din acest șir sunt următoarele: 1,1,2,4,7,13,24,44,81,149,274,504. Tema lui Rică este să găsească termenul de pe locul X. Rică nu știa să zică… regula şirului nostru, de aceea el vă cere ajutorul.
Deduceți regula de formare a șirului și scrieți un program care să afișeze pentru un X dat, elementul din șir de pe poziția X.
Moisil++, 2016
- Fișiere
- Pintilie Vlad
- concurs
- Clasa 10 Probleme diverse Diverse
#1756
Arpsohood
După zile întregi de muncă, vrăjitorul Arpsod a terminat de confecționat noua sa baghetă magică, cea mai puternică de până acum. Ca să o testeze, el s-a gândit la următorul antrenament: își va lua K ținte miscătoare și se va apuca să tragă în ele cu cea mai puternică vrajă a lui, “Blatus Blast”. Fiind o magie foarte solicitantă, vrăjitorul a hotărat că va trage doar de N ori. Arpsod este un trăgător extraordinar, astfel fiecare din cele N lovituri va nimeri exact una din cele K ținte. Într-o sesiune de N lovituri, unele ținte pot fi lovite de mai multe ori iar altele niciodată. Vrăjitorul consideră că sesiunea de antrenament este reușită numai dacă fiecare țintă a fost lovită CEL PUȚIN O DATĂ.
În timp ce se odihnește pentru următoarea sesiune de antrenament, ca să mai treacă timpul, a început să numere în câte moduri ar fi putut lovi țintele astfel încât sesiunea de antrenament să fie una reușită.
Curioși din fire, v-ați apucat și voi să numărați dar, văzând că numărul modalităților devine prea mare, ați decis să vă mulțumiți cu restul împărțirii acestui număr la 666013.
Concursul EMPOWERSOFT, 2016
- Fișiere
- Cristian Dospra
- concurs
- Clasa 10 Probleme diverse Combinatorică
#1831
Blitzcatan
În clasa a 10-a Alina, Bogdan şi Clara se întâlneau în fiecare săptămână să se joace BlitzCatan. Ei aveau la dispoziţie o repriză de 2 ore pe care o foloseau din plin, fiecare joc durând cel puţin 30 de minute. Cei trei prieteni, dornici să reţină cine a câştigat fiecare joc au vrut sa noteze într-un carneţel. Ei s-au temut ca cineva le va citi carneţelul, aşa că au procedat astfel:
- la finalul unui joc
i, câştigătorul c, alege un număr secret \(m_i\)> 0astfel încât \(m_i\)% 3 = c(Alina alege un multiplu de3când câştigă, Bogdan un multiplu de3+1, Clara un multiplu de3+2) - la finalul celor 2 ore, ei calculează unde
Jeste numărul de jocuri, şi noteazăTîn carneţel
Concursul EMPOWERSOFT, 2016
- Fișiere
- Iulia Tamaș
- concurs
- Clasa 10 Probleme diverse Diverse
#1763
Pachete2
Cunoscându-se numărul N de tipuri de produse și cantitățile din fiecare produs, în ordinea în care sosesc de la magazie, să se stabilească numărul maxim de pachete care se pot obține prin alegerea convenabilă a perechilor de produse consecutive și programarea corespunzătoare a automatului, pentru fiecare pereche aleasă.
Concursul EMPOWERSOFT, 2016
- Fișiere
- Rodica Pintea
- concurs
- Clasa 10 Probleme diverse Diverse