Lista de probleme 55

Fie un număr n natural nenul, determinați un număr k și o combinație de semne + sau -(mai exact o succesiune $x_1,x_2,\dots ,x_k$ unde $x_i\in \{-1,1\}$, astfel încat să aibă loc relația: $n=x_1\cdot 1^2+x_2\cdot 2^2+\dots +x_k\cdot k^2$. Să se afișeze o succesiune de k semne + sau - care să îndeplinească relația de mai sus.

Cei n elevi de la grupa pregătitoare au primit câte două cartonaşe, fiecare cartonaş având scris pe el un număr natural. Ei s-au aşezat în cerc şi, la un semnal dat, fiecare a scos la întâmplare un cartonaş din buzunar. Copiii vă roagă să răspundeţi la următoarele întrebări:
1. Care poate fi suma maximă S a numerelor de pe cartonaşele scoase, ştiind că produsul acestora este divizibil cu un număr prim p?
2. Care poate fi lungimea maximă L a unei secvenţe de copii de pe cerc pentru care suma numerelor de pe cartonaşele oricăror doi vecini din secvenţă este pară?

Se citesc de la tastatură numere naturale până la apariția lui zero. Să se determine suma celor pare și câte dintre ele au două cifre.

Se citesc de la tastatură numerele n k, apoi n numere naturale. Să se determine suma celor impare și câte dintre ele se divid cu k.

Se citesc de la tastatură numerele n k, apoi n numere naturale. Să se determine suma celor care se divid cu k și câte dintre ele sunt pare.

Fascinat de Egiptul Antic, Rareș vrea să construiască cât mai multe piramide din cartonașe pătratice identice. El are la dispoziție N cartonașe numerotate de la 1 la N, albe sau gri, așezate în ordinea strict crescătoare a numerelor.

• Prima piramidă o va construi folosind primele trei cartonașe. Baza piramidei va fi formată din cartonașele 1 și 2 așezate alăturat, peste care va așeza cartonașul 3 (vârful piramidei).
• A doua piramidă va avea baza formată din cartonașele 4, 5 și 6 așezate alăturat, deasupra cărora se vor așeza cartonașele 7 și 8, alăturate, peste care se va așeza cartonașul 9 (vârful piramidei).
• Mai departe, va construi în ordine piramidele complete cu bazele formate din 4 cartonașe (cu numerele de la 10 la 13), respectiv 5 cartonașe (cu numerele de la 20 la 24), 6 cartonașe (cu numerele de la 35 la 40) etc., cât timp va putea construi o piramidă completă. De exemplu, dacă Rareș are N=75 cartonașe atunci el va construi piramidele complete 1, 2, 3, 4 și 5 din imaginile următoare. Din cele 75 de cartonașe el va folosi doar primele 55 de cartonașe, deoarece ultimele 20 cartonașe nu sunt suficiente pentru a construi piramida 6, cu baza formată din 7 cartonașe.

Scrieţi un program care să citească numerele naturale N (reprezentând numărul de cartonașe), X (reprezentând numărul unui cartonaș), K (reprezentând numărul de cartonașe albe), numerele celor K cartonașe albe c1, c2, …, cK și care să determine:

a) numărul P al piramidei complete ce conține cartonașul numerotat cu X;
b) numărul M maxim de piramide complete construite de Rareș;
c) numărul C de cartonașe nefolosite;
d) numărul A al primei piramide complete care conține cele mai multe cartonașe albe.

Vrăjitorul Arpsod își dorește să își reamenajeze habitatul. În habitatul acestuia există N munți, fiecare cu o înălțime cunoscută. Fiind un tip cu un foarte dezvoltat simț estetic, el își dorește să remodeleze cei N munți astfel încât să obțină un număr maxim de munți cu aceeași înălțime.

Arpsod are la îndemână o magie ce funcționează astfel: alege oricare doi munți, pe primul îl crește cu o unitate iar pe al doilea îl scade cu o unitate. Un munte poate ajunge la înălțimi negative ( practic se transformă într-o groapă ).

Arpsod își poate folosi magia de un număr infinit de ori.

Vrăjitorul vă cere să determinați numărul maxim de munți ce pot fi aduși la o înălțime egală.

Mihai a găsit pe facebook o poză cu triunghiuri echilaterale aşezate în formă de piramidă, ca în figura de mai jos. El observă că piramida este compusă din mai multe benzi. Prima bandă conţine un triunghi echilateral, a doua bandă conţine 3 triunghiuri echilaterale, dintre care cel din mijloc este cu vârful în jos, a treia bandă conţine 5 triunghiuri echilaterale şi aşa mai departe.

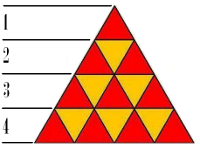
El constată că fiecare triunghi de cea mai mică dimensiune poate fi divizat în mai multe triunghiuri și mai mici prin procedeul de împărțire a unui triunghi. Prin acesta se înțelege unirea mijloacelor laturilor triunghiului, două câte două, printr-un segment, obținându-se astfel 4 triunghiuri mai mici ce compun triunghiul respectiv, ca în figura următoare.

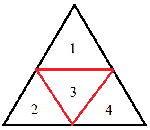
Mihai a analizat acest proces și a stabilit că dacă un triunghi este supus procedeului de împărțire, atunci toate triunghiurile din piramidă de dimensiunea lui vor trece prin acest procedeu. Astfel, el își pune următoarea întrebare: având N piramide, fiecare având un anumit număr de benzi, câte triunghiuri de cea mai mică dimensiune și câte perechi de drepte paralele are fiecare piramidă, după ce s-a executat procedeul de împărțire de M ori pe toate piramidele?

În prima figură o pereche de drepte paralele este formată din dreapta situată între benzile 2-3 și o dreaptă situată între benzile 3-4.

Cunoscând N, M și câte benzi are fiecare piramidă, se cere să se afișeze:

a) câte triunghiuri de cea mai mică dimensiune are fiecare piramidă, după executarea procedeului de împărțire de M ori;
b) câte perechi de drepte paralele are fiecare piramidă, după executarea procedeului de împărțire de M ori.

Un elev a desenat un set format din mai multe pătrate care conțin numere naturale nenule, distincte, consecutive, dispuse în număr egal pe laturi. Pe latura fiecărui pătrat sunt scrise un număr impar de valori. În fiecare pătrat, numerele sunt scrise în ordine crescătoare parcurgând laturile sale, începând din colțul stânga-jos, în sensul invers al acelor de ceasornic. Elevul a numerotat pătratele cu 1, 2, 3 etc., în ordinea strict crescătoare a numărului de valori conținute de fiecare. Diferența dintre cel mai mic număr din pătratul P (1 < P) și cel mai mare număr din pătratul P - 1 este egală cu 1.
Scrieţi un program care rezolvă următoarele două cerinţe:
1. citește un număr natural M și determină numărul K de valori conținute de pătratul numerotat cu M;
2. citește un număr natural N și determină numărul T al pătratului care conține numărul N pe una dintre laturi.

Fie şirul tuturor numerelor naturale de la 1 la un număr oarecare N. Considerând asociate câte un semn (+ sau -) fiecărui număr şi adunând toate aceste numere cu semn se obţine o sumă S. Pentru un S dat, găsiţi valoarea minimă N şi asocierea de semne numerelor de la 1 la N pentru a obţine S în condiţiile problemei.