Lista de probleme 18

Elevii celor două clase de a șaptea din școală merg în excursie. În fiecare clasă sunt câte N elevi. Ovidiu și Mihnea, fiind liderii celor două clase din care fac parte, doresc să analizeze reușita excursiei, în funcție de gradul de compatibilitate dintre elevii participanți la excursie. Pentru a determina acest grad, fiecărui elev din cele două clase îi este atribuit un coeficient de amabilitate.
1. Determinați gradul de compatibilitate dintre cele două clase.
2. Determinați, pentru fiecare elev din clasa lui Ovidiu, numărul de elevi din clasa lui Mihnea cu care acesta poate lega o prietenie durabilă.

Se consideră şirul crescător 1, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, ..., în care fiecare număr natural nenul i apare de 2i-1 ori. Elementele unei matrice A cu M linii şi N coloane au valori astfel încât, parcurgând matricea de sus în jos, pe linii, și de la stânga la dreapta pe fiecare linie, se obțin primii M x N termeni ai șirului precizat. O submatrice a lui A este definită de patru valori, l1, c1, l2, c2 şi este formată din elementele Ai,j cu proprietatea că l1 ≤ i ≤ l2 și c1 ≤ j ≤ c2. Determinaţi suma elementelor pentru fiecare dintre Q submatrice date ale lui A.

Considerăm numerele naturale N, X, Y, M[1], M[2], ..., M[N]. Șirul de numere naturale A[1], A[2], ..., A[N] este numit bun dacă următoarele condiții sunt satisfăcute simultan:

• A[1] OR A[2] OR ... OR A[N] = X, unde OR reprezintă operația sau pe biți.
• A[1] XOR A[2] XOR ... XOR A[N] = Y, unde XOR reprezintă operația sau exclusiv pe biți.
• A[i] AND M[i] = M[i], pentru 1 ≤ i ≤ N, unde AND reprezintă operația și pe biți.

Se dau N, X, Y și M[1], M[2], ..., M[N], cu semnificația din enunț. Să se determine dacă există șiruri bune, respectiv să se determine numărul de șiruri bune, modulo 1.000.000.007.

Se consideră șirul de litere mici ale alfabetului englez A[1], ..., A[N].

Fie succesiunea de caractere alăturate din șir A[x], A[x + 1], ..., A[y], unde 1 ≤ x ≤ y ≤ N, pe care o notăm cu A[x, y]. Pentru oricare literă mică a alfabetului englez l, definim range(l) ca fiind 0, dacă l apare cel mult o dată în A[x, y]. Altfel, valoarea range(l) este egală cu diferența dintre cea mai mare și cea mai mică poziție pe care litera l apare în A[x, y].
Șirul suport asociat lui A[x, y] este șirul de caractere minim lexicografic ce conține fiecare literă l de range(l) ori. Asupra șirului se efectuează două tipuri de operații:

• Actualizare: dându-se litera c și poziția poz, se înlocuiește A[poz] cu c.
• Generare: dându-se perechea x, y, se generează șirul suport al lui A[x, y].

• Dacă C = 1: determinați șirul suport minim lexicografic dintre cele obținute în urma tuturor operațiilor de generare.
• Dacă C = 2: pentru fiecare operație de generare dată, determinați numărul de anagrame distincte ale șirului suport obținut, modulo 1999999973.

Fie a = (a[1], a[2], ..., a[n]) un șir de n numere întregi. Pentru fiecare k ∈ {1,2, ...,n}, definim min[k] = min{a[1], a[2], ... ,a[k]} și max[k] = max{a[1], a[2], ...,a[k]}. Astfel, asociem șirului a un alt șir de intervale închise minmax = ([min[1], max[1]], [min[2], max[2]], ..., [min[n], max[n]]). Vom spune că șirul a este un șir cromatic dacă și numai dacă elementele șirului minmax sunt distincte două câte două, adică nu există două intervale identice în șir. Dându-se un șir a, nu neapărat cromatic, să se determine:

• Numărul de șiruri cromatice NSC ce se pot forma prin rearanjarea elementelor șirului a. Întrucât acest număr poate fi foarte mare, se cere NSC modulo 1.000.000.007.
• Știind că șirul a este cromatic, să se determine poziția p ∈ {1, 2, ..., NSC} a șirului a în lista ordonată lexicografic a tuturor permutărilor cromatice ale lui a.
• Dat fiind q ∈ {1, 2, ..., NSC}, să se determine cel de-al q-lea șir cromatic în ordine lexicografică ce se poate obține prin rearanjarea elementelor șirului a.

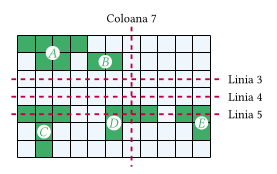
Privit din satelit, Golful Biscayne (Florida) este format din n × m celule pătratice, fiecare celulă fiind umplută fie cu pământ, fie cu apă. Celulele umplute cu pământ sunt grupate în insule: două celule umplute cu pământ fac parte din aceeași insulă dacă și numai dacă se poate ajunge de la una la cealaltă prin deplasare (în sus, jos, stânga sau dreapta) doar pe pământ.

Golful poate fi văzut, astfel, ca o matrice A cu n linii și m coloane (numerotate de la 1), unde A[i][j] = 1 dacă celula de pe linia i și coloana j este umplută cu pământ și A[i][j] = 0 dacă este umplută cu apă.

Spunem că o insulă se află la stânga unei coloane c dacă și numai dacă toate celulele ce intră în alcătuirea insulei sunt strict la stânga coloanei c, adică sunt situate pe coloane strict mai mici decât c. Analog, stabilim dacă o insulă se află la dreapta unei coloane c, respectiv deasupra sau dedesubtul unei linii l. De exemplu, în desenul de mai sus, insulele A, B și C sunt la stânga coloanei 7, insula E este la dreapta coloanei 7, iar insula D nu este nici la stânga, nici la dreapta coloanei 7. De asemenea, insulele A și B sunt deasupra liniei 3, iar insulele C, D și E sunt dedesubtul liniei 4. Mai mult, insulele C, D și E nu sunt nici deasupra, nici dedesubtul liniei 5.

Problema are trei cerințe, cerința de rezolvat fiind dată de T ∈ {1, 2, 3}.

• T = 1. Determinați numărul de celule din golf ce sunt umplute cu pământ.
• T = 2. Determinați numărul de insule din golf ce conțin un număr maxim de celule. Dacă nu există nicio insulă, atunci valoarea acestui număr este 0.
• T = 3. Se dau, în ordine, Q interogări, fiecare fiind descrisă printr-o literă și un număr natural
  nenul p. Determinați valoarea produsului a × b, știind că:
  • Dacă litera este C, atunci a reprezintă numărul de celule din toate insulele ce se află la stânga coloanei p (1 ≤ p ≤ m) și b numărul de celule din toate insulele ce se află la dreapta coloanei p.
  • Dacă litera este L, atunci a reprezintă numărul de celule din toate insulele ce se află deasupra liniei p (1 ≤ p ≤ n) și b numărul de celule din toate insulele ce se află dedesubtul liniei p.

Dexter și-a deschis un laborator nou în care vrea să efectueze o serie de experimente pe șoareci pentru a descoperi leacul pentru cancer. În laborator există N șoareci, care se află așezați într-un cerc și sunt numerotați în ordine de la 0 la N-1. Dexter efectuează, pe rând, M experimente. Pentru fiecare experiment șoarecii care participă la al i-lea experiment formează întotdeauna un interval continuu, exprimat sub forma unei perechi de numere (S[i], F[i]), având semnificația:

• dacă S[i] ≤ F[i], atunci șoarecii S[i], S[i]+1, ..., F[i] participă la experimentul i;
• dacă S[i] > F[i], atunci șoarecii S[i], S[i]+1, ..., N-2, N-1, 0, ..., F[i] participă la experimentul i.

La fiecare pas, Dexter vrea să știe câți din cei N șoareci au participat la toate experimentele efectuate până atunci. Altfel spus, după fiecare al i-lea experiment efectuat, să se determine numărul de șoareci care au participat la toate experimentele 1, 2, ..., i.

Gușteru’ a descoperit într-un dulap un vechi joc de aventură, numit Ijnamuj. Jocul inițial pornește de la nivelul 1, iar scopul este completarea a cât mai multor nivele. Fiecare nivel i are asociată o listă L(i) care conține alte nivele din joc. Pentru a completa nivelul i, Gușteru’ va trebui mai întâi să completeze toate nivelele din lista L(i), în orice ordine dorește el. După completarea oricărui nivel, el poate să completeze orice alt nivel a cărui listă conține numai nivele completate. Pentru că jocul începe de la nivelul 1, lista L(1) va fi mereu vidă, adică completarea lui nu este restricționată de niciun alt nivel. Care este numărul maxim de nivele pe care le poate completa Gușteru’?