Lista de probleme 6
Nivelul concursului: Național
http://www.isjialomita.ro/oni2014/
Grupe
Clasa a V-a Clasa a VI-a Clasa VII-a Clasa VIII-a Clasa a IX-a Clasa a X-a Clasele XI-XII Juniori
#1103
Harta
Pe baza unei imagini preluate din satelit, se realizează harta unei mici localități. Localitatea ocupă o suprafață dreptunghiulară, cu laturile orientate pe direcțiile Nord-Sud, respectiv Est-Vest. Studiind imaginea obținută de la satelit, cartografii au constatat că toate cele k clădiri au forma unor dreptunghiuri distincte. Imaginea poate fi reprezentată sub forma unui tablou cu n•m celule așezate pe n linii numerotate de la 1 la n și m coloane numerotate de la 1 la m.
Numim drum, un dreptunghi al tabloului care străbate întreaga localitate pe direcția Est-Vest și are un număr maxim de linii sau un dreptunghi care străbate întreaga localitate pe direcția Nord-Sud și are un număr maxim de coloane. Drumurile, evident, nu trebuie să treacă prin clădiri.
Cartografii sunt interesați ca pe această hartă să fie reprezentate la scară doar clădirile, nu și drumurile. De aceea, pentru realizarea hărții, lățimile drumurilor au fost reduse la o singură celulă
Tabloul care reprezintă imaginea localității se codifică astfel: 1 pentru o celulă ocupată de o clădire și 0 pentru o celulă neocupată.
Cunoscând n, m și k, precum și tabloul care codifică imaginea, se cere să se determine:
1. Numărul S de celule ocupate de către clădirea pătratică cu latura maximă și numărul de clădiri C alese dintre celelalte k – 1 clădiri, cu proprietatea că fiecare dintre ele “încape” în interiorul clădirii pătratice cu latură maximă, fără să se suprapună peste celulele marginale ale acesteia.
2. Tabloul care reprezintă harta, în urma prelucrării imaginii inițiale.
ONI 2014, Clasa a IX-a
- Fișiere
- Constantin Galatan
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Probleme diverse
#1107
Reflex
La un concurs de robotică, în timpul prezentării, un roboţel cu corp cilindric cu diametrul de o unitate scapă de sub control şi se deplasează într-un ring de formă dreptunghiulară. Ringul este împărţit în N x M pătrate identice, cu latura de o unitate, aşezate pe N linii şi M coloane.
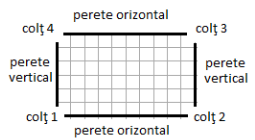 Robotul poate părăsi ringul numai pe la colţuri, acestea fiind numerotate de la
Robotul poate părăsi ringul numai pe la colţuri, acestea fiind numerotate de la 1 la 4, colţul cu numărul 1 fiind cel din stânga jos apoi restul fiind numerotate în sens trigonometric. Suprafaţa ringului este delimitată de exterior prin intermediul a patru pereţi despărţitori: doi pereţi “verticali” (aşezaţi de la colţul 1 la colţul 4, respectiv de la colţul 2 la colţul 3) şi doi pereţi “orizontali” (aşezaţi de la colţul 1 la colţul 2, respectiv de la colţul 3 la colţul 4), fără a bloca ieşirile, ca în desenul alăturat.
1 sub un unghi de 45 grade şi cu o viteză de un pătrat/s. Ciocnirile cu pereţii sunt considerate perfect elastice (robotul nu-şi pierde din viteză) iar unghiul de incidenţă este egal cu cel de reflexie.
Se cere să se determine:
a) după câte secunde şi prin ce colţ al ringului va ieşi robotul;
b) de câte ori se ciocneşte robotul de pereţii orizontali şi verticali, rezultând o schimbare de direcţie, până la ieşirea din ring.
ONI 2014, Clasa a IX-a
- Fișiere
- Lucian Silaghi
- concurs
- Clasa 9 Probleme diverse Probleme diverse
#1104
qvect
Se consideră N vectori cu elemente întregi, numerotați de la 1 la N, sortați crescător, fiecare vector având un număr precizat de elemente.
Să se răspundă la Q întrebări de tipul:
a) 1 i j, cu semnificaţia: care este minimul dintre modulele diferențelor oricăror două elemente, primul element aparținând vectorului numerotat cu i, iar cel de al doilea element aparținând vectorului numerotat cu j ?
b) 2 i j, cu semnificația: care este valoarea ce se găsește pe poziția mediană în vectorul obținut prin interclasarea vectorilor având numerele de ordine i,i+1,…,j (i<j).
ONI 2014, Clasa a IX-a
- Fișiere
- Eugen Nodea
- concurs
- Clasa 9 Probleme diverse Probleme diverse
- Interclasare
- Cautare binara
#1105
TG
Fie un număr natural N. Spunem că (a, b, c) este un triplet geometric limitat de N, dacă a, b și c sunt trei numere naturale astfel încât 1 ≤ a < b < c ≤ N și \( b = \sqrt {a \cdot c} \).
Să se determine numărul tripletelor geometrice limitate de numărul natural N.
ONI 2014, Clasa a IX-a
- Fișiere
- concurs
- Clasa 9 Probleme diverse Probleme diverse
- Descompunere in factori
#1106
Progresie
Să se determine un șir strict crescător, cu lungimea N, format din numere naturale nenule, \( 1 ≤ a_1 < a_2 < a_3 < … < a_N ≤ [2 \cdot N \cdot \sqrt{N}] \), cu proprietatea că oricare trei termeni distincți ai șirului nu sunt în progresie aritmetică, adică pentru oricare numere naturale i, j şi k cu 1 ≤ i < j < k ≤ N, este îndeplinită condiţia: \( a_i + a_j \neq 2 \cdot a_j \). Prin [x] s-a notat partea întreagă a lui x.
De exemplu, pentru N = 5, cel mai mare termen al șirului va trebui să fie mai mic sau egal cu \( [2 \cdot 5 \cdot \sqrt{5} ] \), adică aN ≤ 22, deci o soluție este: 1, 2, 4, 5, 10.
ONI 2014, Clasa a IX-a
- Fișiere
- Ciprian Chesca
- concurs
- Clasa 9 Probleme diverse Probleme diverse
#1108
Traseu
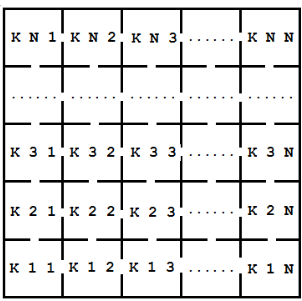 Într-un oraș există un hotel de formă cubică, cu
Într-un oraș există un hotel de formă cubică, cu N etaje, numerotate de la 1 la N. Suprafața fiecărui etaj K (1 ≤ K ≤ N) este pătratică și este împărțită în N x N camere identice alăturate, dispuse pe N linii și N coloane, fiecare cameră având drept etichetă un triplet de numere naturale (K L C) (K=etajul, L=linia, C=coloana, 1 ≤ L, C ≤ N), ca în imaginea alăturată.
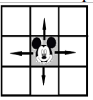 Dintre cele
Dintre cele N x N x N camere ale hotelului, una este specială deoarece în ea locuiește de mult timp un șoricel. Fiind isteț, el știe eticheta camerei în care se află precum și eticheta camerei în care bucătarul hotelului depozitează alimente.
Studiind hotelul, șoricelul a constatat că pe fiecare etaj, din orice cameră poate intra în toate camerele care au un perete comun cu aceasta (existând un mic orificiu pentru aerisire).
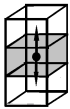 De asemenea, șoricelul a constatat că din fiecare cameră (situată la etajele
De asemenea, șoricelul a constatat că din fiecare cameră (situată la etajele 2, 3, …, sau N-1) poate intra în camera situată imediat deasupra ei și în camera situată imediat sub ea.
Fiind un șoricel binecrescut, el nu intră în nicio cameră ocupată de clienți ca să nu-i deranjeze. Hotelul având mulți clienți, șoricelul trebuie să-și găsească cel mai scurt traseu de la camera lui la camera cu alimente, traseu care să treacă printr-un număr minim de camere, toate neocupate.
Se cere să se determine:
a) numărul de camere prin care trece cel mai scurt traseu al șoricelului de la camera lui la camera cu alimente (inclusiv camera lui şi camera cu alimente);
b) etichetele camerelor prin care trece traseul determinat la punctul a).
ONI 2014, Clasa a IX-a
- Fișiere
- Carmen Minca
- concurs
- Clasa 10 Structuri de date liniare Coada