Lista de probleme 6

Olivius d’Info a primit de ziua lui o stivă şi s-a bucurat foarte tare. S-a tot gândit ce să facă cu ea şi a inventat un joc de logică pentru colegii lui de clasă.

În prima fază el a scris mai multe bileţele, conţinând fiecare câte o permutare a primelor n numere naturale nenule: 1, 2, 3, … , n. Bileţelele scrise conţin permutări pentru diferite valori ale lui n.

A clasificat aceste permutări în permutări stivuite şi permutări nestivuite.

O permutare este stivuită dacă se poate obţine pe parcursul introducerii în stivă a numerelor 1, 2, 3, ...,n în această ordine, prin extragerea elementelor, în ordinea indicată în permutare.

O permutare nestivuită este o permutare care NU se poate obţine prin procedeul de mai sus.

Respectând procedeul lui Olivius, pentru n=4, permutarea stivuită (2,1,3,4) se obţine astfel:

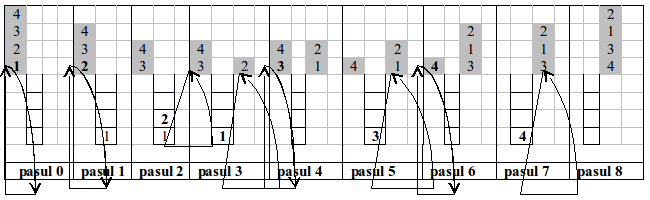
Succesiunile (3,1,2,4) şi (4,2,1,3) sunt permutări nestivuite.

În faza a doua, unele bileţele au fost scurtate din stânga şi/sau din dreapta. Astfel, din permutarea stivuită (2,1,3,4) se pot obţine succesiuni de lungime mai mică: (1,3,4), (2,1,3), (1,3), (3) etc.

Orice succesiune care aparţine unei permutări stivuite, poate aparţine şi unei permutări nestivuite. De exemplu, succesiunea (2,1,3) aparţine atât permutării stivuite (2,1,3,4), cât şi permutării nestivuite (4,2,1,3).

Dându-se mai multe succesiuni de numere naturale distincte, determinaţi, pentru fiecare dintre acestea, dacă aparţin cel puţin unei permutări stivuite.

Spionul 008 vrea să găsească o locație secretă în junglă, având asupra lui un dispozitiv de localizare. Iniţial spionul se află la intrarea în junglă pe nivelul 1 şi cu fiecare pas, el avansează de la nivelul i la nivelul i+1, ajungând la locaţia secretă, aflată pe ultimul nivel, în poziţia u faţă de marginea stângă a nivelului curent. Pentru a ajunge în locaţia secretă, el poate să se deplaseze cu o poziţie spre Sud-Est (codificat cu caracterul E) sau spre Sud-Vest (codificat cu caracterul V), trecând de pe nivelul i pe nivelul i+1 cu viteză constantă. Numărul de poziţii de pe un nivel creşte cu unu faţă de nivelul anterior, conform imaginii alăturate. Numim traseu o succesiune formată din caracterele E sau V, corespunzătoare deplasării spionului de pe nivelul 1 la locaţia secretă. Pentru exemplul din figura alăturată succesiunea de caractere VEEVE reprezintă un traseu ce corespunde locaţiei secrete din poziţia 4 a nivelului 6.

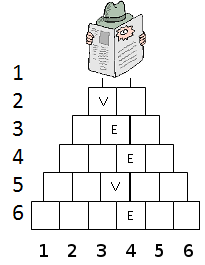
Cunoscând succesiunea de caractere corespunzătoare unui traseu, determinaţi:
a) poziţia locației secrete de pe ultimul nivel;
b) numărul de trasee distincte pe care le poate urma spionul plecând din poziţia inițială pentru a ajunge în locaţia secretă corespunzătoare traseului dat. Două trasee se consideră distincte dacă diferă prin cel puţin o poziţie.

Costel are o mare pasiune pentru rezolvarea cubului Rubik, atât de mare încât a început să facă cercetări și calcule diverse pornind de la acest joc. Ultima lui idee, inspirată de cubul Rubik, folosește un cub de latură 2 unități, compus din 8 cuburi cu latura de o unitate (cub unitate), având fețele exterioare colorate. Fiecare cub unitate are 3 fețe exterioare şi fiecare dintre acestea este colorată cu una din cele 10 culori disponibile, codificate prin cifrele de la 0 la 9.

Figura 1	Figura 2

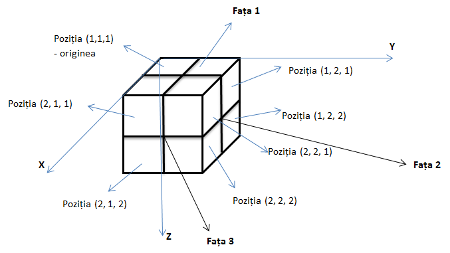
Identificarea cuburilor unitate se face conform specificaţiilor din Figura 1. Cubul care nu este vizibil în Figura 1 are coordonatele (1, 1, 2). Cubul lui Costel permite efectuarea următoarelor tipuri de mutări, asemănătoare cu cele din cubul Rubik:

M1: Paralelipipedul 1 conține cuburile unitate de coordonate: (1, 1, 1); (1, 2, 1); (2, 1, 1); (2, 2, 1). Acesta este un disc așezat orizontal și poate fi rotit cu 90 de grade către dreapta, în sensul acelor de ceasornic.
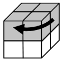M2: Paralelipipedul 2 conține cuburile unitate de coordonate: (1, 1, 2); (1, 2, 2); (2, 1, 2); (2, 2, 2). Acesta este un disc așezat orizontal și poate fi rotit cu 90 de grade către dreapta, în sens invers acelor de ceasornic.
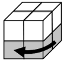M3: Paralelipipedul 3 conține cuburile unitate de coordonate: (1, 1, 1); (2, 1, 1); (1, 1, 2); (2, 1, 2). Acesta este un disc așezat vertical și poate fi rotit cu 90 de grade către planul îndepărtat, în sens invers acelor de ceasornic.
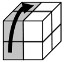M4: Paralelipipedul 4 conține cuburile unitate de coordonate: (1, 2, 1); (2, 2, 1); (1, 2, 2); (2, 2, 2). Acesta este un disc așezat vertical și poate fi rotit cu 90 de grade către planul îndepărtat, în sensul acelor de ceasornic.

Prin configurație se înțelege memorarea culorii fiecărei fețe exterioare a celor 8 cuburi unitate, deci culorile celor 24 de feţe exterioare. Aplicând o succesiune validă de mutări se obține o altă configurație.

Pentru ușurința memorării unei configurații, Costel utilizează desfășurarea în plan a celor 6 fețe ale cubului său după modelul din Figura 2, care ilustrează modul în care sunt dispuse fețele în desfăşurare. Fiecare faţă a cubului conţine patru feţe exterioare ale cuburilor unitate având, în ordine, coordonatele specificate în figură.

Fiind date o configuraţie iniţială şi o configuraţie finală ale jocului, determinați numărul minim de mutări prin care se poate ajunge de la configurația inițială la configurația finală şi succesiunea corespunzătoare de mutări prin care se poate obţine configuraţia finală.

Nu e un secret pentru nimeni faptul că Mireluş se antrenează în timpul liber cu probleme de algoritmică. De curând a aflat că un număr natural N, pentru care există două numere naturale nenule A şi B (B>1) astfel încât N = A^B, se numeşte putere. Mireluş şi-a propus să determine numărul de puteri din intervalul [X, Y], unde X şi Y sunt numere naturale nenule.

Cum probabil v-aţi imaginat deja, Mireluş nu a reuşit să rezolve această problemă şi a decis să ceară ajutorul Olimpiei D’Info. Pentru a fi sigur că nici ea nu greşeşte, i-a dat un set de intervale şi i-a cerut să determine pentru fiecare interval numărul de puteri corespunzător.

Dându-se numărul de intervale T şi pentru fiecare din cele T intervale cele două extremităţi, determinaţi numărul de puteri corespunzător fiecărui interval dat de Mireluş Olimpiei.

Suleiman I s-a confruntat în anul 1548 cu mari probleme interne. În acel an, el a primit vestea că într-una din regiunile Imperiului se pregăteşte o răscoală. Harta Imperiului este realizată sub forma unui tablou bidimensional cu n linii şi m coloane, iar fiecare element al tabloului corespunde unei regiuni a Imperiului. În fiecare regiune erau deja cantonaţi soldaţi, dar pentru a preîntâmpina răscoala sultanul decide ca toţi cei k soldaţi din Garda Imperială să fie trimişi în regiuni, întărindu-le pe cele păzite de mai puţini soldaţi. Distribuirea lor respectă următoarele reguli:

• Dacă există o singură regiune cu număr de soldaţi mai mic decât al tuturor celorlalte regiuni, trimite un soldat în această regiune.
• Dacă există mai multe regiuni cu acelaşi număr minim de soldaţi, trimite un soldat în regiunea care iniţial avea un număr mai mic de soldaţi. Dacă mai multe regiuni aveau acelaşi număr iniţial de soldaţi, se trimite un soldat în regiunea cu indicele liniei mai mic, iar dacă regiunile sunt pe aceeaşi linie, în regiunea cu indicele coloanei mai mic.

Suleiman continuă distribuirea soldaţilor din garda imperială în regiuni conform celor precizate anterior, până la epuizarea soldaţilor din Garda Imperială.

Cunoscându-se n, m şi k reprezentând numărul de linii, numărul de coloane, respectiv numărul de soldaţi din Garda Imperială, precum şi numărul de soldaţi existent deja în regiunile Imperiului, să se determine:
a) numărul de regiuni din Imperiu în care vor fi trimişi soldaţii din Garda Imperială, respectiv numărul minim de soldaţi care se vor găsi într-o regiune, după trimiterea soldaţilor din Garda Imperială;
b) distanța maximă între două regiuni în care au fost trimiși soldaţi ai Gărzii Imperiale. Distanța între o regiune A și o regiune B se calculează folosind formula |LA- LB| + |CA- CB|, unde (LA ,CA) reprezintă coordonatele regiunii A, precizate prin numărul liniei și coloanei, respectiv (LB ,CB) reprezintă coordonatele regiunii B, precizate prin numărul liniei și coloanei.

Olimpia D’Info a găsit o placă gravată ce conţine mai multe cuvinte scrise cu semne grafice necunoscute, fiecare cuvânt fiind format din exact 5 semne grafice. Studiind cu atenție cuvintele, a dedus că în scrierea acestora sunt utilizate 12 semne grafice distincte şi a asociat câte o literă mică din alfabetul englez fiecărui semn. După asociere, a stabilit pentru fiecare semn o complexitate, scriind literele în ordinea crescătoare a complexităților pe care le-a stabilit anterior. Olimpia consideră că această ”complexitate” este cel mai potrivit criteriu de ordonare lexicografică.

Cunoscând ordinea semnelor și cuvintele de pe placă determinaţi:
a) Numărul de cuvinte distincte existente pe placă.
b) Şirul de cuvinte ordonat lexicografic, conform criteriului formulat de Olimpia.