Lista de probleme 33

În acest an evenimentul ”Hour of Code” a înregistrat un număr record de participanți din țara noastră. În cadrul acestui eveniment una dintre cele mai accesate aplicații a fost Lightbot, care a permis elevilor să-și testeze abilitățile de programare.

Aplicația Lightbot are N nivele, numerotate consecutiv de la 1 la N, în ordinea strict crescătoare a complexității lor. Lightbot a permis fiecărui participant să înceapă cu orice nivel strict mai mic decât N-1 și să sară peste un singur nivel, fără a finaliza codul, trecând la nivelul următor celui sărit. La finalizarea cu succes a codului corespunzător nivelului curent, participantul este promovat la nivelul imediat următor. Fiecare participant a început scrierea codurilor la un nivel P și a sărit peste un nivel L (P < L < P + K), finalizând K nivele memorate ca o succesiune de numere naturale de forma P, P+1,..., L-1, L+1,..., P+K. Succesiunile de nivele finalizate de participanți au fost memorate în fișierul lightbot.in. Succesiunile corespunzătoare participanților nu se intercalează în fișier.

Scrieţi un program care citeşte succesiunile corespunzătoare nivelelor finalizate de participanții care au jucat Lightbot și determină:

1. numărul total de participanți;
2. numărul celui mai dificil nivel care a fost rezolvat de un număr maxim de participanți;
3. pentru fiecare participant, numărul nivelului sărit de acesta.

Lui Mihai îi place matematica distractivă, sau poate mai mult distracția decât matematica. Pentru a scăpa de teme, el a inventat operația ”smile” notată cu semnul ☺, operație care se aplică numerelor naturale nenule conform exemplelor de mai jos:

• 6☺4=210
• 9☺2=711
• 8☺5=313
• 7☺6=113
• 6☺6=12
• 6☺10=416
• 43☺1500=14571543
• 23☺23=46

Profesorul de matematică i-a promis nota 10 pentru invenție, numai dacă știe să determine corect numărul divizorilor pari pentru rezultatul obținut prin operația ”smile”. Astfel, Mihai a primit N perechi de numere (a,b) pentru care trebuie să calculeze a☺b și să determine dacă rezultatul obținut are divizori pari.

Scrieți un program care citește un număr natural N și N perechi de numere naturale (a,b) și afișează:

a) pentru fiecare pereche de numere (a,b), rezultatul a☺b;
b) cel mai mic și cel mai mare rezultat a☺b care nu are divizori pari.

Iepurașul Coconaș vrea să ajungă la grădina cu morcovi. Pentru aceasta el trebuie să traverseze prin salturi o zonă cu proprietăți speciale. Zona este formată din N căsuțe numerotate de la 1 la N, dispuse una după cealaltă, iar fiecare căsuță conține un număr natural ce reprezintă cantitatea de energie necesară iepurașului pentru a sări într-o altă căsuță.

Iepurașul pleacă dintr-o anumită căsuță și se deplasează, de la stânga la dreapta, spre grădina cu morcovi după următoarele reguli:

• numărul înscris în căsuța în care se află iepurașul reprezintă numărul de căsuțe peste care el va sări;
• dacă numărul înscris în căsuța în care se află iepurașul este număr prim, atunci energia lui se dublează şi va sări peste un număr dublu de căsuţe;
• numărarea căsuțelor peste care va sări se face de la stânga la dreapta și începe cu căsuța imediat următoare. Astfel, dacă iepurașul se află în căsuța a treia și numărul înscris în această căsuță este 5, iepurașul va ajunge în căsuța cu numărul de ordine 13 (13=3+2*5).
• dacă iepurașul ajunge într-o căsuță care conține numărul 0, el rămâne acolo pentru că nu mai are energie să sară mai departe, altfel el continuă să sară după regulile descrise mai sus;
• iepurașul ajunge la grădina cu morcovi dacă ultimul salt pe care îl face depășește căsuța N.

Scrieți un program care citește trei numere naturale P, N și K iar apoi N numere naturale și determină:

1) dacă iepurașul poate ajunge sau nu, la grădina cu morcovi pornind din căsuța K și numărul de salturi pe care le face iepurașul pornind din căsuța K;
2) căsuța de pornire a iepurașului, astfel încât drumul parcurs de el să traverseze un număr maxim de căsuțe. Pentru a determina numărul de căsuțe se vor lua în calcul: căsuța de pornire, toate căsuțele peste care iepurașul a sărit și toate căsuțele în care a ajuns în urma salturilor. Iepurașul poate porni din oricare căsuță. În cazul în care există două sau mai multe căsuțe de pornire care conduc la același număr maxim de căsuțe traversate se va lua în considerare căsuța cu numărul de ordine cel mai mic.

În țara lui Piticot cuvintele au doar două litere, prima fiind o majusculă (literă mare) iar a doua o minusculă (literă mică). Piticii Mi și Gi se distrează și își trimit mesaje ascunzând cuvintele în cadrul unor secvențe transmise sub forma unor șiruri de litere. Piticul Mi scrie și trimite un mesaj piticului Gi respectând următoarele reguli:

• un mesaj conține una sau mai multe secvențe;
• orice literă care apare în mesaj, de cel puțin două ori, pe poziții alăturate, este numită terminator;
• o secvență se încheie când s-a întâlnit o succesiune de litere terminator;
• cuvântul este format din prima majusculă și ultima minusculă din secvență, fără a lua în seamă litera terminator a secvenței;
• o secvență ascunde un cuvânt dacă terminatorul său se repetă de exact două ori și dacă conține cel puțin o literă mare și o literă mică, ignorând terminatorul de secvență;
• costul unui cuvânt este egal cu numărul total de apariții al celor două litere din care este format, în cadrul secvenței în care a fost ascuns, luând în considerare inclusiv literele terminator.

De exemplu secvența s f u E e t R u E E ascunde un cuvânt deoarece conține și majuscule și minuscule, iar litera terminator de secvență, E, se repetă de exact două ori. Secvența ascunde cuvântul Eu, iar costul cuvântului este 5 (3 litere E + 2 două litere u).

La primirea mesajului, piticul Gi determină, pentru fiecare majusculă, costul maxim al cuvintelor care încep cu aceasta.

Scrieţi un program care determină:

1) numărul de secvențe trimise care nu ascund cuvinte;
2) cuvintele din mesaj, în ordinea în care au fost trimise de piticul Mi;
3) pentru fiecare majusculă, câte cuvinte care încep cu ea au costul maxim determinat de Gi.

După descoperirea ruinelor unei cetăți medievale, arheologii au hotărât restaurarea acesteia, începând cu zidul principal. Acesta este format din N piloni, fiecare cu lățimea de 1 metru, așezați unul lângă altul (lipiți). Se cunoaște înălțimea, în metri, a fiecărui pilon dar, din păcate, nu toți mai sunt acum la același nivel.

Pentru restaurarea zidului, arheologii dispun de cărămizi care au lățimea de câte 1 metru și lungimi variabile, exprimate în metri. Sunt disponibile oricâte cărămizi, de oricare lungime. Considerăm că toate cărămizile disponibile și toți pilonii care alcătuiesc zidul au aceeași grosime, de 1 metru.

Restaurarea constă în două etape:

• în prima etapă, toți pilonii cu înălțimea mai mare sau egală cu H se retează, aducându-se astfel la înălțimea H, ceilalți, mai scunzi, păstrându-și înălțimea inițială;
• în a doua etapă se aduc toți pilonii la aceeași înălțime, umplându-se golurile dintre ei cu cărămizi, astfel încât zidul să devină compact; din motive neînțelese, arheologii vor așeza cărămizile “culcate”, fiecare dintre acestea ocupând, eventual, spațiul aflat deasupra mai multor piloni.

Arheologii au analizat situația, independent, pentru Q valori posibile ale lui H.

Pentru fiecare dintre cele Q valori alese pentru înălțimea H, se cere să se determine numărul minim de cărămizi necesare restaurării zidului, independent, pornind de la înălțimile inițiale ale pilonilor.

Ben are un teren pe care se află o pădure cu arbori seculari. Acolo vrea să-şi construiască o cabană, însă el fiind ecologist nu vrea să taie niciun arbore, ci vrea să găsească cea mai mare suprafaţă dreptunghiulară fără arbori. El caută o suprafaţă dreptunghiulară străjuită doar în colţuri de arbori şi cu laturile paralele cu axele de coordonate. Ben cunoaşte coordonatele tuturor arborilor din pădure şi vă roagă să-l ajutaţi să găsească aria dreptunghiului cu suprafaţă maximă care are arbori doar în cele patru colțuri.

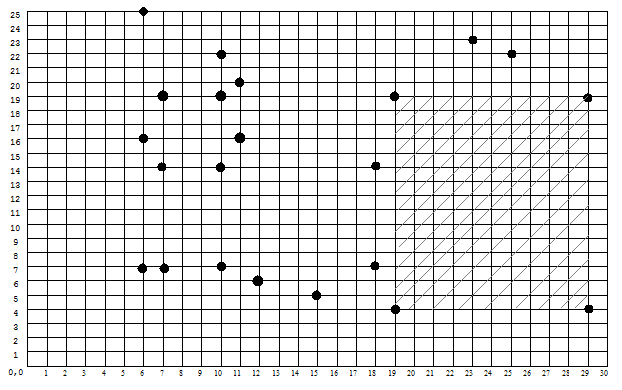
Cunoscând numărul arborilor din pădure şi coordonatele acestora, se cere să se determine aria dreptunghiului de suprafaţă maximă cu copaci doar în cele 4 colţuri, unde Ben intenţionează să-şi construiască cabana.

Fie n un număr natural nenul.

Să considerăm o expresie de forma: x[1]-x[2]-x[3]-...-x[n]

Se ştie că scăderea nu este o operaţie asociativă, adică x[1]-(x[2]-x[3])≠(x[1]-x[2])-x[3].

Ca urmare, prin plasarea unor perechi de paranteze în expresie, putem obţine diferite valori.
Pentru problema noastră, vom denumi scădere o expresie de forma de mai sus în care pot apărea şi paranteze rotunde care se închid corect. Valoarea unei scăderi se obţine efectuând operaţiile de scădere în ordine de la stânga la dreapta; dacă apar paranteze, se efectuează mai întâi operaţiile din paranteze.

Date fiind valorile x[1], x[2], …, x[n] care intervin în scădere, scrieţi un program care să rezolve următoarele două cerinţe:

1. să se determine valoarea maximă a unei scăderi (obţinută prin inserarea convenabilă a unor paranteze rotunde în expresia x[1]-x[2]-x[3]-...-x[n]), precum şi o scădere având valoare maximă.
2. să se determine valoarea unei scăderi specificate.

Un proprietar vinde un teren de formă dreptunghiulară împărțit în MxN parcele de formă pătrată cu lungimea laturii de o unitate. Fiecare parcelă costă V lei. Vlad s-a interesat și a aflat pentru fiecare din parcelele terenului care este valoarea de revânzare. El constată că unele parcele i-ar putea aduce profit, iar altele i-ar aduce pierdere. Fiind isteț, negociază cu proprietarul să cumpere atâtea parcele de teren câte pot fi împrejmuite cu un singur gard de lungime egală cu 2M+2N unități. Terenul are pe fiecare din cele patru laturi acces la drumul exterior, pe o porțiune de lungime egală cu o unitate. Vlad negociază astfel încât terenul achiziționat să conțină și cele patru parcele de acces la exterior.

Cunoscând M și N – dimensiunile terenului, V – prețul de cumpărare al fiecărei parcele, x_nord, x_sud, y_vest și y_est – pozițiile parcelelor cu acces la drumul exterior și A[i][j], 1≤i≤M și 1≤j≤N – valorile de revânzare pentru fiecare parcelă, să se determine:

a) Profitul P_arie_minimă pe care-l poate obține Vlad după cumpărarea și apoi revânzarea suprafeței de teren de arie minimă, împrejmuită conform condițiilor negociate.
b) Profitul maxim P_max pe care-l poate obține Vlad după cumpărarea și apoi revânzarea unei suprafețe de teren împrejmuită conform condițiilor negociate.

Definim o modificare procentuală de preț ca fiind o pereche (c p) formată dintr-un caracter din {‘+‘,‘-‘} și un număr natural p. Dacă c = ‘+‘ atunci are loc o scumpire iar dacă c = ‘-‘ atunci are loc o ieftinire a unui preț, iar numărul p reprezintă procentul de modificare a prețului.

Exemple de modificări procentuale de preț: (+ 35) – reprezintă scumpirea unui preț cu 35%; (– 50) – reprezintă ieftinirea unui preț cu 50%.

Unui preț inițial i se poate aplica o succesiune de n modificări procentuale de preț obținându-se un preț final. Numim ciclu de preț de lungime n o succesiune de n modificări procentuale de preț, cu proprietatea că prețul final este egal cu prețul inițial.

Să se scrie un program care citește un număr natural n și determină numărul de cicluri de preț de lungime n distincte ce conțin cel puțin o dată o modificare procentuală cunoscută (C P).

Ne aflăm în secția de vopsitorie a uzinei Toyota Motor unde inginerii japonezi prezintă ultimul tip de robot industrial de vopsire. În dorința de a evidenția calitatea și viteza de execuție a roboților, inginerii folosesc pentru demonstrație o tablă de dimensiunea n×n, împărțită în pătrate cu latura egală cu 1, reprezentată sub forma unui tablou bidimensional cu n linii şi n coloane.

Un robot utilizat pentru vopsire are două brațe telescopice care se deplasează de-a lungul unei axe. Fiecare braț poate vopsi într-o unitate de timp un singur pătrat. La momentul de timp t=0 robotul primește comanda de a se poziționa într-un pătrat specificat prin coordonatele (x,y).

În funcție de traiectoria de deplasare roboții folosiți sunt de două tipuri. La momentul de timp t robotul de tip 1 vopsește pătratele aflate la coordonatele: (x-t,y+t) și (x+t,y-t), iar robotul de tip 2 vopsește pătratele aflate la coordonatele: (x+t,y+t) și (x-t,y-t). Pentru vopsirea unui pătrat se consumă 1 litru de vopsea.

Pe tablă sunt așezați m roboți.

Cunoscând pentru cei m roboți coordonatele inițiale (x[i],y[i]), i=1,…,m, se cere să se determine:

a) Cantitatea totală de vopsea care a fost folosită de roboți după t unități de timp
b) Numărul minim de unități de timp necesare formării primului dreptunghi cu arie nenulă. Un dreptunghi corect format este rezultatul intersecției a două traiectorii paralele a doi roboți de tip 1 cu două traiectorii paralele a doi roboți de tip 2, iar colțurile dreptunghiului sunt 4 pătrate care au fost vopsite de doi roboți de tipuri diferite.