Lista de probleme 14
Nivelul concursului: Județean
Grupe
Clasa a V-a Clasa a VI-a Clasa VII-a Clasa VIII-a Clasa a IX-a Clasa a X-a Clasele XI-XII
#1084
Tren
Un elev în clasa a V-a, Rareş, s-a gândit să studieze mersul trenurilor ce trec prin gara din oraşul său, într-o zi. Gara are 2 linii, numerotate cu 1 şi 2, pe care sosesc şi pleacă trenurile. În acea zi, în gară sosesc T trenuri. Pentru fiecare tren din cele T, Rareş cunoaşte linia L pe care va sosi, momentul sosirii, adică ora H şi minutul M, precum şi durata de timp S de staţionare (exprimată în minute). El a decis ca perioada de studiu a celor T trenuri să înceapă cu momentul sosirii primului tren în gară din cele T şi să se încheie odată cu momentul plecării ultimului tren din cele T.
Din sala de aşteptare Rareş poate vedea cele 2 linii. Rareş are însă o problemă: atunci când un tren se află în gară pe linia 1, el nu poate vedea trenul staţionat în acelaşi timp pe linia 2. De exemplu, dacă un tren ajunge în gară pe linia 1 la ora 14:21 şi staţionează 5 minute atunci trenul va pleca din gară la ora 14:26. Astfel, în intervalul de timp [14:21-14:26], Rareş nu poate vedea ce se întâmplă pe linia 2. Trenul de pe linia 2 va putea fi vizibil începând cu minutul următor, adică de la 14:27.
Scrieţi un program care să determine pentru un număr T de trenuri care trec prin gară în perioada de studiu din acea zi:
- numărul maxim de trenuri
Zcare au staţionat pe aceeaşi linie; - numărul
Xde trenuri pe care Rareş le vede; - durata de timp maximă
Y(exprimată în număr de minute consecutive), din perioada de studiu, în care Rareş nu a văzut niciun tren.
OJI 2010, Clasa a V-a
- Fișiere
- Cristina Sichim
- concurs
- Clasa 9 Algoritmi elementari Probleme diverse
#1088
Zar
 Zarul folosit la diverse jocuri este un cub care are desenat pe fiecare faţă a sa
Zarul folosit la diverse jocuri este un cub care are desenat pe fiecare faţă a sa 1, 2, 3, 4, 5 sau 6 puncte. Pe un zar nu există două feţe cu acelaşi număr de puncte şi suma punctelor de pe oricare două feţe opuse este egală cu 7.
Pe o masă de joc este desenat un traseu în formă de pătrat, cu latura de dimensiune n. Fiecare latură a traseului este împărţită în n pătrăţele identice, care au latura egală cu cea a zarului. Zarul este aşezat iniţial în colţul din stânga sus al traseului şi apoi rostogolit de pe o faţă pe alta, din pătrăţel în pătrăţel, de-a lungul traseului parcurs în sensul acelor de ceasornic.
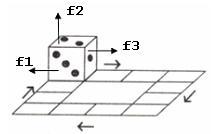
În orice moment ne-am uita la zar, putem vedea numărul punctelor desenate pe trei din feţele sale (aşa cum se vede în desenul de mai sus).
Notăm cu f1 faţa cubului orientată spre noi, f2 faţa superioară a cubului, respectiv cu f3 faţa laterală din dreapta. Pentru exemplul din figură: n=4, faţa dinspre noi (f1) conţine trei puncte, faţa superioară (f2) conţine două puncte, faţa laterală din dreapta (f3) conţine un punct, iar sensul de deplasare este cel precizat prin săgeţi.
Cunoscând dimensiunea n a traseului şi numărul punctelor de pe cele trei feţe ale zarului în poziţia iniţială, determinaţi după k rostogoliri numărul punctelor ce se pot observa pe fiecare din cele trei feţe ale zarului.
OJI 2010, Clasa a VII-a
- Fișiere
- Cristina Iordaiche
- concurs
- Clasa 9 Probleme diverse Probleme diverse
#1090
Secvente2
Mariei îi plac numerele prime şi puterile numerelor prime. Pornind de la un număr prim p, ea construieşte noi numere, fiecare număr construit fiind un produs de forma py (y număr natural nenul) sau q∙pm, m număr natural şi q un număr prim, numindu-le numere p-prime. De exemplu, numerele 2, 3, 4, 5, 6, 7, 8, 10, 12, 13, 14, 16, 17 sunt primele 13 numere 2-prime deoarece 2=21, 3=3•20, 4=22, 5=5•20, 6=3•21, 7=7•20, 8=23, 10=5•21, 12=3•22, 13=13•20, 14=7•21, 16=24, 17=17•20.
Într-o zi Maria a găsit o foaie de hârtie, pe care era scris un şir format din n numere naturale nenule.
Cum pe lângă numerele p-prime ea este pasionată şi de secvenţe, şi-a pus următoarea întrebare: câte secvenţe sunt pe foaie cu următoarele proprietăţi:
- conţin exact
knumerep-prime; - încep şi se termină cu un număr
p-prim.
În plus, Maria doreşte să ştie care este poziţia de început şi cea de final, pentru fiecare secvenţă descoperită, relative la şirul scris pe foaia de hârtie.
Scrieţi un program care să citească mai multe seturi de date, fiecare set fiind format din numerele n, p, k, cu semnificaţiile din enunţ, şi şirul cu n elemente a1, a2, a3, … an, numerele Mariei. Programul va determina pentru fiecare set de date numărul secvenţelor ce conţin exact k numere p-prime, precum şi poziţiile de început şi de final ale acestor secvenţe în şirul din set.
OJI 2010, Clasa a VIII-a
- Fișiere
- concurs
- Clasa 9 Probleme diverse Probleme diverse
#1083
Sir5
Se generează un şir de numere naturale ai cărui primi termeni sunt, în ordine:
1, 12, 21, 123, 231, 312, 1234, 2341, 3412, 4123, 12345, 23451,...
Deduceţi regula după care sunt generaţi termenii şirului şi scrieţi un program care să citească numerele naturale k, x, a şi b şi care să determine:
a) ultima cifră a sumei tuturor termenilor şirului care sunt formaţi din cel mult k cifre;
b) succesorul termenului x în şirul dat, x fiind un termen al şirului;
c) numărul de termeni ai şirului care au cifra cea mai semnificativă egală cu a şi nu conţin în scrierea lor cifra b.
OJI 2010, Clasa a V-a
- Fișiere
- Carmen Minca
- concurs
- Clasa 9 Algoritmi elementari Cifrele unui număr
#1080
Livada
Norocosul Gigel tocmai a primit în dar de la bunicul său, Nelu, o imensă plantaţie de pomi fructiferi. Fost profesor de geometrie, Nelu a plantat în mod riguros pomii fructiferi pe m rânduri paralele, iar pe fiecare rând a plantat exact câte n pomi fructiferi. Însă, din motive mai mult sau mai puţin obiective, domnul Nelu nu a plantat pe fiecare rând toţi pomii de acelaşi soi, ci din mai multe soiuri diferite. Soiurile de pomi plantaţi în livadă sunt codificate cu numere naturale cuprinse între 1 şi p.
Cuprins de febra rigurozităţii matematice şi de cea a statisticii, Gigel a definit noţiunea de soi majoritar astfel: dacă pe un rând k format din n pomi fructiferi avem cel puţin [n/2]+1 pomi de acelaşi soi x, atunci spunem că soiul x este soi majoritar pe rândul k (prin [y] se înţelege partea întreagă a numărului real y).
Cunoscând numerele m, n şi p, precum şi soiul fiecărui pom de pe fiecare rând al plantaţiei, ajutaţi-l pe Gigel să determine:
- pe câte rânduri din livadă există un soi majoritar;
- care este cel mai mare număr de pomi de acelaşi soi plantaţi în poziţii consecutive pe un rând.
OJI 2010, Clasa a IX-a
- Fișiere
- Radu Boriga
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme diverse
- Element majoritar
#1081
Numar3
Se dă un număr raţional strict pozitiv q, sub formă de fracţie zecimală.
Să se determine două numere naturale a şi b astfel \( q= \frac{a}{b} \) încât iar modulul diferenţei dintre a şi b să fie minim.
OJI 2010, Clasa a IX-a
- Fișiere
- Stelian Ciurea
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme diverse
- Numere mari
#1085
Loto
La Loteria Naţională există N bile inscripţionate cu numere naturale, nenule, distincte de cel mult 4 cifre. Şeful de la loterie primeşte o cutie în care se află cele 6 bile extrase la ultima rundă, restul bilelor neextrase fiind puse într-un seif. Deoarece are o fire poznaşă, el scoate din cutie bila pe care este înscris numărul cel mai mic şi o păstrează în buzunarul hainei sale. În locul ei va pune o bilă neextrasă, aflată în seif, având numărul cel mai apropiat de aceasta. Apoi continuă operaţia şi scoate din cutie şi bila pe care este înscris numărul maxim extras iniţial, pe care o va pune în celălalt buzunar al său. De asemenea o va înlocui cu o altă bilă neextrasă iniţial, aflată în seif, având numărul cel mai apropiat de aceasta.
Realizaţi un program care afişează în ordine crescătoare numerele de pe bilele aflate în cutie după modificările făcute de şef.
OJI 2010, Clasa a VI-a
- Fișiere
- Dana Lica
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme diverse
#1086
Submit
Vasilică se antrenează pe un site de probleme cu evaluare online. Când el trimite pe site soluţia la o problemă, aceasta este evaluată pe un anumit număr de teste. Punctajul obţinut la problema respectivă va fi egal cu suma punctajelor obţinute la fiecare test. Punctajele asociate testelor pot fi diferite. În plus, dacă problema a fost complet rezolvată (a obţinut punctaj maxim la toate testele), Vasilică primeşte şi un bonus.
Vasilică poate trimite soluţia la o problemă de mai multe ori. Când trimite soluţia prima dată, punctajul se calculează în modul prezentat anterior. Când trimite soluţia a doua oară, Vasilică va fi penalizat cu două puncte (adică din punctajul total obţinut la problemă se scad două puncte). Când trimite soluţia a treia oară penalizarea este de 4 puncte, a patra oară de 6 puncte ş.a.m.d. Observaţi că la fiecare nouă încercare penalizarea creşte cu două puncte.
Date fiind rezultatele obţinute pe teste de Vasilică la fiecare soluţie trimisă, să se determine punctajul maxim pe care el l-a obţinut la problema respectivă.
OJI 2010, Clasa a VI-a
- Fișiere
- Emanuela Cerchez
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme diverse
#1089
Cladiri1
Institutul de Fizică a Pământului studiază efectele unui potenţial cutremur folosind simulări computerizate. Harta plană a clădirilor de pe un teritoriu oarecare este reprezentată folosind coordonatele GPS în plan, longitudine şi latitudine, faţă de un reper considerat de coordonate (0,0), ca în figura de mai jos.
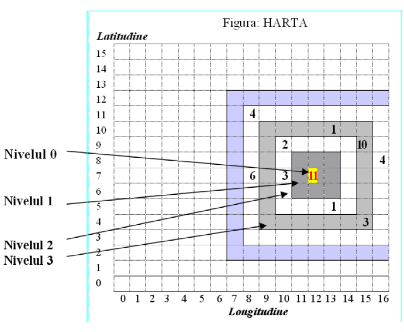
Fiecare dintre clădirile aflate pe hartă, au două coordonate GPS, (Longitudine, Latitudine) şi un Grad de rezistenţă la cutremure.
Un cutremur se poate produce în orice punct de coordonate de pe hartă, numit centrul seismului şi are o anumită intensitate. Unda de şoc se propagă sub forma unor pătrate concentrice cu centrul seismului, numite nivele (nivelul 0 reprezintă centrul seismului, nivelul 1 primul pătrat concentric, nivelul 2 al doilea pătrat concentric şi aşa mai departe). Intensitatea slăbeşte la fiecare pătrat concentric cu centrul seismului cu câte o unitate. Clădirile sunt afectate de cutremur doar dacă gradul lor de rezistenţă la cutremur este mai mic sau egal cu intensitatea cutremurului în poziţia clădirii.
Scrieţi un program care să citească coordonatele centrului seismului şi intensitatea sa în acel punct, precum şi coordonatele clădirilor şi gradul lor de rezistenţă la cutremur, şi apoi să determine:
a) numărul N total de clădiri afectate;
b) numărul M maxim de clădiri afectate pe un nivel;
c) numerele nivelelor cu M clădiri afectate, în ordinea crescătoare a numerelor acestor nivele.
OJI 2010, Clasa a VIII-a
- Fișiere
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme diverse
#1091
Expozitie
Ilinca este o fetiţă căreia îi place foarte mult să deseneze; ea a făcut multe desene pe care le-a numerotat de la 1 la d şi apoi le-a multiplicat (toate copiile poartă acelaşi număr ca şi originalul după care au fost făcute). În vacanţă s-a hotărât să-şi deschidă propria expoziţie pe gardul bunicilor care are mai multe scânduri; pe fiecare scândură ea aşează o planşă (un desen original sau o copie). Ilinca ţine foarte mult la desenele ei şi doreşte ca fiecare desen să apară de cel puţin k ori (folosind originalul şi copiile acestuia). Ilinca se întreabă în câte moduri ar putea aranja expoziţia. Două moduri de aranjare sunt considerate distincte dacă diferă cel puţin prin numărul unei planşe (de exemplu: 2 1 3 3 este aceeaşi expoziţie ca şi 2 3 1 3, dar este diferită de 2 1 3 1 şi de 1 3 3 1).
Cunoscând n numărul de scânduri din gard, d numărul desenelor originale şi k numărul minim de apariţii al fiecărui desen, să se determine în câte moduri poate fi aranjată expoziţia, ştiind că Ilinca are la dispoziţie oricâte copii doreşte.
OJI 2010, Clasa a X-a
- Fișiere
- Lucia Miron
- concurs
- Clasa 10 Probleme diverse Combinatorică
- Numere mari
- Combinatorica
- Stars and Bars