Lista de probleme 14

Ana şi Bogdan au găsit la bunicul lor o cutie cu N beţe de aceeaşi lungime. După câteva minute de joacă urmează cearta. Bunicul le-a propus să rupă cele N beţe și apoi Ana să primească fragmentele din mâna stângă, iar Bogdan fragmentele din mâna dreaptă. Zis şi făcut. Copiii au luat fragmentele, le-au numerotat fiecare cu numere de la 1 la N, le-au măsurat şi acum îşi doresc să lipească fragmentele primite, dar mai au nevoie de câteva informaţii.

Cunoscând N numărul de beţe, a1, a2,…, aN lungimile fragmentelor primite de Ana şi b1, b2,…, bN lungimile fragmentelor primite de Bogdan, să se scrie un program care să determine:

a) lungimea iniţială a beţelor;
b) lungimea celui mai lung băţ care se poate obţine prin lipirea unui fragment aparţinând Anei cu un fragment care aparţine lui Bogdan;
c) numărul beţelor de lungime maximă care se pot obţine prin lipirea unui fragment aparţinând Anei cu un fragment care aparţine lui Bogdan.

Jocul betaşah se joacă folosindu-se doar piese asemănătoare damelor clasicului şah, numite tot dame. Suprafaţa de joc are o formă triunghiulară şi este formată din N*(N+1)/2 pătrate identice dispuse pe N rânduri şi N coloane. Rândurile se numerotează de sus în jos, de la 1 la N. Coloanele se numerotează de la stânga la dreapta, de la 1 la N. Primul rând conţine un singur pătrat, al doilea rând conţine două pătrate alăturate,…, al N-lea rând conţine N pătrate alăturate, ca în suprafeţele de joc cu N=6 din figurile de mai jos. Din cele N*(N+1)/2 pătrate, K sunt gri, iar restul sunt albe. Poziţia fiecărui pătrat de pe suprafaţa de joc este dată de rândul şi coloana în care acesta este situat.

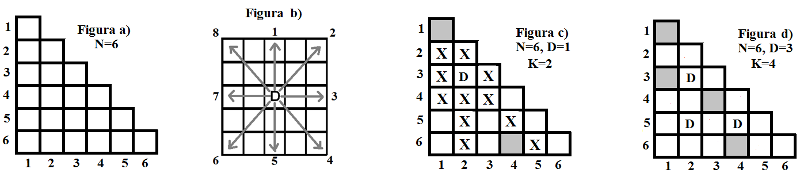
Pe suprafaţa de joc sunt aşezate D dame în D pătrate albe distincte, ocupându-le. Într-un pătrat alb poate fi aşezată o singură damă, iar într-un pătrat gri nu poate fi aşezată nicio damă. Poziţia unei dame pe suprafaţa de joc este dată de poziţia pătratului alb în care este aşezată dama.

Damele pot accesa orice pătrat alb neocupat situat pe direcţiile: verticală, orizontală sau diagonală, numerotate de la 1 la 8 în figura b). Accesul pe o direcţie se face trecând din pătrat alb în pătrat alb (doar pătrate albe neocupate) până la întâlnirea unui pătrat gri sau a unui pătrat alb ocupat de o altă damă sau până la terminarea suprafeţei de joc.

Numim pătrat accesibil orice pătrat alb neocupat (de pe suprafaţa de joc) care ar putea fi accesat de cel puţin una din cele D dame.

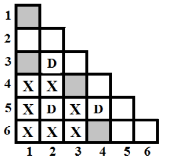
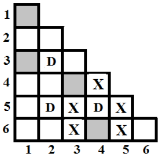
De exemplu, pentru suprafaţa de joc din figura c) numărul de pătrate accesibile (marcate cu X) de pe suprafaţă este 11; pentru suprafaţa de joc cu N=6, D=3 şi K=4 din figura d) numărul de pătrate accesibile de pe suprafaţă este 13. În figura e) sunt marcate cu X pătratele accesibile fiecărei dame de pe suprafaţa de joc din figura d).

Pătratele accesibile damei din rândul 3 şi coloana 2	Pătratele accesibile damei din rândul 5 şi coloana 2	Pătratele accesibile damei din rândul 5 şi coloana 4	Pătratele accesibile de pe suprafaţa de joc
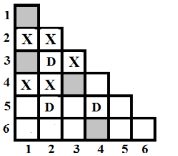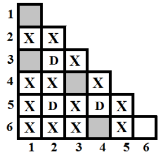Figura e)

Scrieţi un program care să citească numerele naturale N, D, K, poziţiile damelor şi ale pătratelor gri pe suprafaţa de joc şi care să determine:
a) numărul maxim M de pătrate albe conţinute de un rând al suprafeţei de joc;
b) numărul P de pătrate accesibile de pe suprafaţa de joc.

Andrei se descurcă foarte bine la geometrie şi de aceea născoceşte tot felul de jocuri pe care le testează cu Alexandru, colegul său de bancă. Pentru a pregăti noul joc cu trei niveluri, Andrei desenează pe o foaie de matematică reperul cartezian xOy şi mai multe puncte distincte. Fiecare punct desenat are atât abscisa x, cât şi ordonata y, numere întregi.

La primul nivel, Alexandru determină numărul maxim de puncte (dintre cele desenate) aflate pe una dintre axele sistemului cartezian sau pe o dreaptă paralelă cu una dintre cele două axe.
La al doilea nivel, Alexandru consideră toate punctele desenate a căror abscisă x şi ordonată y verifică cel puţin una dintre relaţiile x=y sau x+y=0 şi apoi calculează câte drepte distincte trec prin cel puţin două dintre aceste puncte.

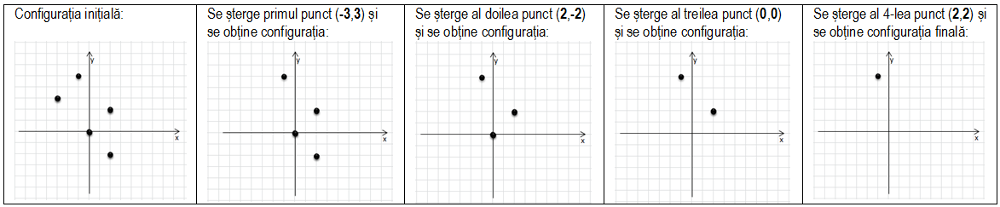
La al treilea nivel, Alexandru numără şi şterge punctele din 3 în 3 (primul, al 4-lea, al 7-lea etc.), începând cu cel mai din stânga punct desenat şi continuând către dreapta. Dacă două sau mai multe puncte au aceeaşi abscisă, el le numără pe acestea de jos în sus (începând de la punctul cu ordonata cea mai mică). Când a ajuns cu număratul la cel mai din dreapta punct continuă cu cel mai din stânga punct rămas.

Alexandru se opreşte cu numărarea şi ştergerea când rămâne un singur punct desenat pe foaie.

Scrieţi un program care citeşte numărul natural nenul N, apoi cele 2*N numere întregi ce reprezintă coordonatele celor N puncte şi determină:

a) NRP, numărul maxim de puncte (dintre cele desenate) aflate pe una dintre axele sistemului cartezian sau pe o dreaptă paralelă cu una dintre cele două axe;
b) NRD, numărul de drepte distincte care trec prin cel puţin două dintre punctele desenate a căror abscisa x şi ordonată y verifică cel puţin una dintre relaţiile x=y sau x+y=0;
c) XP reprezentând abscisa punctului rămas pe foaie la sfârşitul celui de-al treilea nivel al jocului.

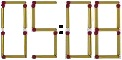Lui Gigel, elev în clasa a V-a, îi place grozav de tare să se joace cu cifrele, cu numerele şi creează tot felul de probleme pe care apoi încearcă să le rezolve. Acum se joacă cu o cutie de chibrituri şi formează cu ele cifre. Apoi privirea i-a căzut pe cadranul unui ceas electronic şi a văzut că cifrele sunt formate din segmente orizontale şi verticale şi a început să formeze cu chibriturile cifrele care indică ora (vezi figura). Şi imediat şi-a pus o întrebare: “oare dacă am n chibrituri puse vertical şi m chibrituri puse orizontal, care este ora minimă pe care o pot forma cu aceste chibrituri?”

Fiind date un număr n de chibrituri verticale şi un număr m de chibrituri orizontale, să se scrie un program care determină numărul de ore posibile, ora minimă şi ora maximă care se pot forma cu aceste chibrituri, în modul indicat mai sus, utilizând toate chibriturile respective şi nemodificând orientarea acestora.

Având mai multe cuburi la dispoziţie, Crina şi Rareş au hotărât să construiască clădiri prin alipirea a două sau mai multor turnuri. Turnurile au fost obţinute prin aşezarea cuburilor unul peste celălalt. Înălţimea unui turn este dată de numărul de cuburi din care este format.
Clădirile construite au fost aşezate în linie, una lângă alta formând astfel o stradă, pe care cei doi copii se vor plimba.

Pentru numerotarea clădirilor Crina şi Rareş au stabilit următoarele reguli:

• Crina porneşte dintr-un capăt al străzii, iar Rareş din celălalt capăt al acesteia; fiecare dintre ei traversează strada complet, trecând prin dreptul fiecărei clădiri
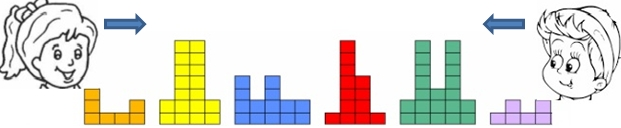
• Crina lipeşte pe fiecare clădire câte un bileţel pe care scrie înălţimea turnurilor din care aceasta este construită, în ordinea în care ea le vede când trece prin dreptul lor (de exemplu, pentru imaginea de mai sus, Crina va lipi pe prima clădire un bileţel pe care va scrie numărul 3112 deoarece, primul turn e format din 3 cuburi, următoarele două turnuri ale acestei clădiri sunt formate din câte un cub iar cel de-al patrulea turn e format din 2 cuburi);
• Rareş va proceda la fel, dar începe plimbarea din celalalt capăt al străzii. În exemplul din imagine, el va lipi pe prima clădire pe care o întâlneşte un bileţel pe care scrie numărul 2121.
• La finalul plimbării, Crina şi Rareş îşi dau seama că există clădiri pe care au lipit amândoi bileţele cu numere identice.

a) Care este înălţimea celui mai înalt turn şi care este numărul clădirilor care au în construcţia lor un astfel de turn?
b) Care este numărul clădirilor pe care cei doi copii au lipit bileţele cu numere identice?
c) Care este cel mai mic număr de cuburi necesar pentru a completa clădirile astfel încât, pe fiecare clădire, bileţelul pe care îl va lipi Crina să conţină acelaşi număr cu cel pe care îl va lipi Rareş? Cuburile din care a fost construită iniţial clădirea nu se pot muta.

După ce au descoperit ascunzătoarea piratului Spânu, marinarii de pe corabia “Speranţa” au hotărât să ofere sătenilor o parte din comoara acestuia. Întrucât comoara avea un număr nelimitat de bani din aur, numiţi galbeni, singura problemă a marinarilor a fost regula după care să împartă banii.

După îndelungi discuţii au procedat astfel: i-au rugat pe săteni să se aşeze în ordine la coadă şi să vină, pe rând, unul câte unul pentru a-şi ridica galbenii cuveniţi. Primul sătean a fost rugat să îşi aleagă numărul de galbeni, cu condiţia ca acest număr să fie format din exact K cifre. Al doilea sătean va primi un număr de galbeni calculat astfel: se înmulţeşte numărul de galbeni ai primului sătean cu toate cifrele nenule ale acelui număr, rezultatul se înmulţeşte cu 8 şi apoi se împarte la 9 păstrându-se doar ultimele K cifre ale câtului împărţirii. Dacă numărul obţinut are mai puţin de K cifre, atunci acestuia i se adaugă la final cifra 9, până când se completează K cifre.

Pentru a stabili câţi galbeni primeşte al treilea sătean, se aplică aceeaşi regulă, dar pornind de la numărul de galbeni ai celui de-al doilea sătean. Regula se aplică în continuare fiecărui sătean, plecând de la numărul de galbeni primiţi de săteanul care a stat la coadă exact în faţa lui.

Cunoscând numărul de galbeni aleşi de primul sătean, determinaţi numărul de galbeni pe care îl va primi al N-lea sătean.

Ana şi Bogdan au inventat jocul “Compar”. Ana scrie pe tablă o secvenţă formată din N numere naturale distincte cuprinse între 1 şi N, apoi compară fiecare două numere învecinate din secvenţă scriind între ele semnul < sau semnul >, după caz.
De exemplu, dacă secvenţa de pe tablă este 6 4 2 1 3 5, după compararea elementelor învecinate şi inserarea semnelor în secvenţă, Ana obţine:
6>4>2>1<3<5
După aceea Ana şterge cele N elemente ale secvenţei şi păstrează numai semnele, astfel:
>>><<
La final, Ana îi arată lui Bogdan şirul semnelor şi îi cere să reconstituie secvenţa de numere naturale scrisă iniţial pe tablă.

Cunoscând şirul semnelor construit de Ana, scrieţi un program care să îl ajute pe Bogdan să reconstituie secvenţa de numere naturale distincte scrisă iniţial pe tablă.

Considerăm un şir de numere a1, a2, …, aN. O secvenţă nevidă în acest şir este de forma ai, ai+1, …, aj, unde i ≤ j. De exemplu, pentru N=4 şi şirul 2 3 4 3, secvenţele nevide sunt: 2, 2 3, 2 3 4, 2 3 4 3, 3, 3 4, 3 4 3, 4, 4 3, 3. Definim puterea unui element ai ca fiind numărul de secvenţe care-l conţin pe ai şi în care ai este strict mai mare decât celelalte elemente ale fiecăreia dintre respectivele secvenţe. Astfel în şirul 2 3 4 3 puterea elementului a1 este 1 (fiind maxim doar în secvenţa formată din el însuşi), a elementului a2 este 2 (a2 fiind maxim în secvenţele 2 3 şi 3), a elementului a3 este 6 (fiind maxim în secvenţele 2 3 4, 2 3 4 3, 3 4, 3 4 3, 4 şi 4 3), iar a elementului a este 1.

Scrieţi un program care determină puterea cea mai mare a unui element din şirul dat, precum şi numărul de elemente din şir care au cea mai mare putere.

O clepsidră este un dispozitiv folosit pentru a măsura timpul. Clepsidra este alcătuită din două incinte de sticlă, conectate printr-un tub fin. Una dintre incinte este umplută cu nisip, acesta scurgându-se în cea de-a doua incintă, cu o viteză constantă. Clepsidra poate fi întoarsă, pentru a măsura o altă perioadă de timp.

Arheologii au descoperit un dispozitiv, pe care l-au denumit clepsidru, format din n clepsidre identice, suprapuse, numerotate de la 1 la n, prin care nisipul poate circula de la o clepsidră la alta datorită forţei gravitaţionale.

Studiind acest obiect, arheologii au constatat că :

• dispozitivul poate fi utilizat atât în poziţia 1, când clepsidrele sunt în ordinea 1, 2 ,…, n cu clepsidra n aşezată pe sol, cât şi în poziţia 2, când clepsidrele sunt în ordinea n, n-1,…, 1 cu clepsidra 1 aşezată pe sol;
• viteza de trecere a nisipului de la o incintă la alta, a aceleiaşi clepsidre, este de 1 bob de nisip/secundă, pentru toate clepsidrele, indiferent de poziţie;
• trecerea clepsidrului dintr-o poziţie în alta presupune răsturnarea acestuia şi reaşezarea boabelor de nisip;
• timpul de trecere a boabelor de nisip de la o clepsidră la alta este 0.

Arheologii studiază comportarea clepsidrului realizând două experimente diferite, după cum urmează:

a) Se aşează clepsidrul în poziţia 1, se introduc în incinta de sus a clepsidrei 1 un număr b de boabe de nisip şi se determină după câte secunde vor ajunge toate boabele de nisip în incinta de jos a ultimei clepsidre;
b) Se aşează clepsidrul în poziţia 1, se introduc în incinta de sus a clepsidrei 1 un număr b de boabe de nisip, apoi se aşează clepsidrul în k stări consecutive, o stare fiind caracterizată de valorile si şi pi , 1 ≤ i ≤ k, ce reprezintă numărul de secunde, respectiv poziţia, în care este menţinut nemişcat clepsidrul, iar la final se determină numărul de boabe de nisip din incintele fiecărei clepsidre.

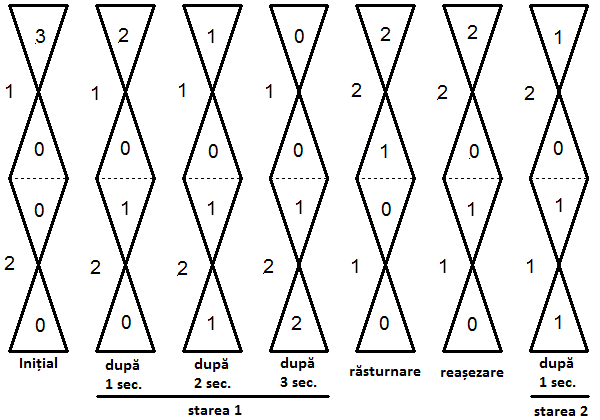Spre exemplu, dacă clepsidrul este format din n=2 clepsidre, iar în incinta de sus a primei clepsidre se introduc b=3 boabe de nisip, la primul experiment se va obţine valoarea 4.

La al doilea experiment se aşează clepsidrul în k=2 stări, caracterizate prin s1=3, p1=1; s_{2=1, p2=2.}

Numărul de boabe de nisip din clepsidre va evolua ca în figura alăturată.

Să se scrie un program care citeşte valorile n şi b, precum şi valorile k, si, pi , 1 ≤ i ≤ k, şi calculează valorile obţinute de arheologi la realizarea celor două experimente.

Se consideră un şir A=(A1, A2, ..., AN), format din N numere naturale nenule. Două numere se consideră vecine dacă se află pe poziţii alăturate (Ai are ca vecini pe Ai-1 şi Ai+1, pentru orice 1<i<N, A1 are ca vecin doar pe A2, iar AN are ca vecin doar pe AN-1).

Dacă două elemente vecine Ai, Ai+1 (1≤i<N) au cel puţin o cifră comună, ele se pot unifica. Procedeul de unificare constă în eliminarea din numerele Ai şi Ai+1 a tuturor cifrelor comune şi adăugarea prin alipirea numărului obţinut din Ai+1 la numărul obţinut din Ai, formându-se astfel un nou număr. Numărul Ai va fi înlocuit cu noul număr, iar numărul Ai+1 va fi eliminat din şir.

De exemplu, numerele Ai=23814 şi Ai+1=40273 au cifrele 2, 3, 4 comune, după unificare obţinem Ai=817, iar Ai+1 este eliminat; observaţi că dacă după eliminarea cifrelor comune, numerele încep cu zerouri nesemnificative, acestea vor fi eliminate, apoi se realizează alipirea.

Dacă în urma eliminării cifrelor comune, unul dintre numere nu mai are cifre, atunci numărul rezultat va avea cifrele rămase în celălalt. Dacă în urma eliminării cifrelor comune atât Ai cât şi Ai+1 nu mai au cifre, atunci ambele numere vor fi eliminate din şir, fără a fi înlocuite cu o altă valoare.

Ordinea în care se fac unificările în şir este importantă: la fiecare pas se alege prima pereche de elemente vecine Ai Ai+1 care poate fi unificată, considerând şirul parcurs de la stânga la dreapta. (De exemplu, considerând Ai=123, Ai+1=234, Ai+2=235, se unifică Ai cu Ai+1 => Ai=14, iar unificarea cu următorul număr nu mai este posibilă).

Cunoscându-se şirul celor N numere naturale, să se determine:

a) cifra care apare cel mai frecvent în scrierea tuturor celor N numere; dacă există mai multe cifre cu aceeaşi frecvenţă de apariţie maximă, se va reţine cea mai mică cifră.
b) şirul obţinut prin efectuarea unui număr maxim de unificări, după regulile descrise în enunţ.