Lista de probleme 14
Nivelul concursului: Județean
http://olimpiada.info/oji2015/
Grupe
Clasa a V-a Clasa a VI-a Clasa VII-a Clasa VIII-a Clasa a IX-a Clasa a X-a Clasele XI-XII
#1139
Covor
Bunica Marei țese un covor. Mara urmărește cu mare atenție modelul și încearcă să-l reconstituie pe caietul de matematică. Modelul este format din romburi. Primul romb, de indice 1, are latura formată din două pătrățele, al doilea romb, de indice 2, are latura formată din trei pătrățele etc. Un romb de indice i are latura formată din i+1 pătrățele.
Romburile sunt unite, consecutiv, ca în exemplul din imaginea alăturată. Săgețile indică sensul în care bunica țese covorul.
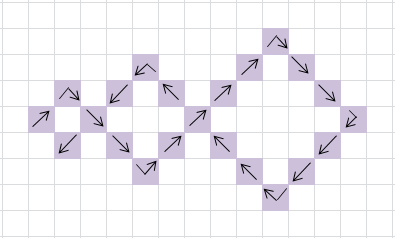
Ca să nu uite modelul, Mara scrie pe caiet, începând cu 1, numere consecutive care să indice modul în care țese bunica covorul.
În exemplul următor este reprezentat modul în care se țese un model format din patru romburi.
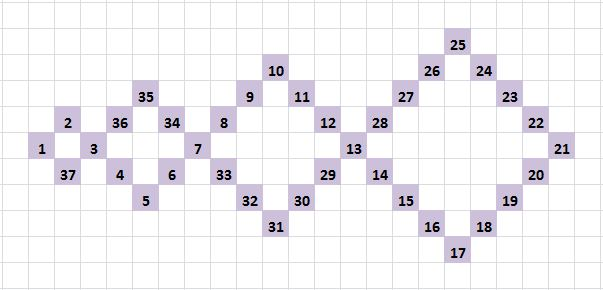
Cunoscându-se numerele n și k să se determine:
1. numărul maxim de romburi complete care pot forma modelul unui covor, descris cu ajutorul unui șir format din maximum n numere naturale consecutive (primul număr din șir fiind 1);
2. cel mai mic indice al unui romb ce conține numărul k.
OJI 2015, Clasa a VI-a
- Fișiere
- Cristina Sichim
- concurs
- Clasa 9 Algoritmi elementari Probleme diverse
#1132
Defrag
Discul dur (hard disk) este un dispozitiv utilizat pentru stocarea datelor. Stocarea se face pe o suprafață magnetică dispusă pe platane rotunde metalice. Pe un platan, datele sunt organizate în piste și sectoare, iar zona aflată la intersecția dintre o pistă și un sector poartă denumirea de cluster.
Un cluster poate avea două stări: liber, dacă nu conține date, sau ocupat, atunci când conține date.
Un platan se numește defragmentat dacă toți clusterii ocupați de pe fiecare pistă sunt așezați în ordine consecutivă. Defragmentarea se realizează prin mutarea unor clusteri ocupați și are rolul de a micșora timpul de acces la date. Mutarea unui cluster reprezintă transferul datelor de la un cluster ocupat către un cluster liber de pe aceeași pistă.
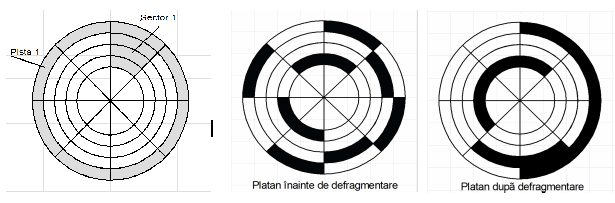
Cunoscând numărul de piste P și de sectoare S al unui platan, numărul și poziția clusterilor ocupați, să se scrie un program care determină :
1. numărul de piste care au toți clusterii liberi;
2. numărul minim de mutări de clusteri, pentru fiecare pistă în parte, astfel încât platanul să devină defragmentat.
OJI 2015, Clasa a IX-a
- Fișiere
- Ciprian Chesca
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Probleme diverse
#1142
Lasere
Se consideră un teren reprezentat printr-o matrice cu n linii şi n coloane având elemente numere naturale. În fiecare element al matricei este memorată înălţimea zonei de teren corespunzătoare ca poziţie elementului respectiv. Pe acest teren sunt amplasate m lasere, în poziţii cunoscute. Un laser este îndreptat spre unul dintre cele 4 puncte cardinale, codificate prin numere astfel: Nord prin valoarea 1, Est prin valoarea 2, Sud prin valoarea 3 şi respectiv Vest prin valoarea 4. Fiecare laser va executa o singură tragere şi ca urmare va scădea cu 1 valorile tuturor elementelor din matrice din direcţia sa de tragere, exceptând poziţia laserului respectiv.
După efectuarea tuturor tragerilor, se caută poziţiile tuturor gropilor şi ale tranşeelor.
Numim groapă un element din matrice pentru care toate cele 8 elemente învecinate pe linie, coloană sau diagonale au valori mai mari sau egale decât el.
Numim tranşee o secvenţă maximală formată din două sau mai multe gropi situate pe aceeaşi linie, pe coloane consecutive. Secvenţa se numeşte maximală dacă nu mai poate fi prelungită la niciunul dintre capete.
Cunoscând configuraţia terenului şi amplasarea laserelor, să se rezolve una dintre următoarele două cerinţe:
1. să se determine numărul de gropi din teren, după executarea tragerilor;
2. să se determine numărul de tranşee existente, după executarea tragerilor.
OJI 2015, Clasa a VII-a
- Fișiere
- Vlad Laurentiu Nicu
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Probleme diverse
#1131
Arc
Irinuca a descoperit un nou joc pe calculator. Pe ecran sunt plasate pe o linie n bile colorate. Culorile bilelor sunt codificate cu numere naturale. Un subșir de bile alăturate având toate aceeași culoare se numește secvență. O secvență va conține numărul maxim de bile alăturate având aceeași culoare. Lungimea unei secvențe este egală cu numărul de bile din care este compusă.
Irinuca are la dispoziție un arc special. Trăgând cu arcul asupra unei bile, dacă aceasta face parte dintr-o secvență de lungime cel puțin egală cu 3, întreaga secvență va fi eliminată, iar bilele din dreapta secvenței se vor deplasa spre stânga pentru a umple “golul” lăsat de bilele eliminate. Dacă imediat în stânga și în dreapta secvenței eliminate se găseau două secvențe având aceeași culoare și dacă secvența obținută din unirea acestora după eliminare are o lungime cel puțin egală cu 3, atunci va fi și ea eliminată la rândul ei. Procesul continuă până când secvențele din stânga și dreapta unei secvențe tocmai eliminate au culori diferite sau până când lungimea secvenței obținute prin alăturare este mai mică decât 3 sau până când în stânga ori în dreapta unei secvențe eliminate nu se mai găsesc bile sau până sunt eliminate toate bilele de pe ecran.
Scopul jocului este de a elimina cât mai multe bile de pe ecran. Cum Irinuca încă nu se pricepe prea bine la acest joc și-a stabilit o strategie. Va trage cu arcul întotdeauna asupra unei bile ce face parte din secvența de lungime maximă de pe ecran. Dacă sunt mai multe astfel de secvențe, ea va alege cea mai din stânga secvență de lungime maximă. Dacă toate secvențele de pe ecran au lungimi mai mici decât 3, Irinuca nu va mai putea elimina nici una din ele și jocul se încheie.
Cunoscând numărul de bile și culorile fiecărei bile de pe ecran se cere să se determine:
1. numărul de secvențe de bile care se aflau inițial pe ecran;
2. numărul de bile care rămân neeliminate de pe ecran și culorile bilelor rămase în ordine pe ecran la finalul jocului.
OJI 2015, Clasa a IX-a
- Fișiere
- Carmen Popescu
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme cu secvențe
#1140
Ordine
Gigel a primit de ziua lui un joc cu bile. Jocul conţine n bile numerotate cu numerele naturale distincte de la 1 la n. Jucându-se, Gigel a amestecat bilele astfel încât acum ele nu mai sunt în ordine. Ca să le pună înapoi în cutia jocului, Gigel ia de pe masă bilele una câte una, şi le pune în cutie formând un şir. Însă Gigel se joacă şi acum, astfel încât el nu pune bilele la rând, una după alta, ci are o regulă pe care o respectă cu stricteţe. Astfel, Gigel încearcă să plaseze fiecare bilă pe care a luat-o de pe masă exact la mijlocul şirului de bile deja format. Dacă acest lucru nu este posibil (șirul are lungime impară), atunci el plasează bila la sfârşitul şirului de bile deja format. După ce toate bilele au fost puse în cutie, Gigel îşi dă seama că nu a notat ordinea în care a luat bilele de pe masă şi, în mod firesc, îşi pune problema dacă nu cumva poate deduce acest lucru din şirul de bile pe care tocmai l-a format.
Cunoscându-se numărul de bile şi configuraţia finală a bilelor în şir să se determine:
1. numărul ultimei bile luate de pe masă;
2. ordinea în care bilele au fost luate de pe masă.
OJI 2015, Clasa a VI-a
- Fișiere
- Marinel Serban
- concurs
- Clasa 9 Probleme diverse Probleme diverse
#1144
Pavare1
Ca în mai toate poveștile, Făt-Frumos a căutat o Cosânzeană și a găsit-o, dar tatăl ei i-a cerut să-i paveze drumul de lungime N care leagă castelele sale. Dalele cu care va pava drumul au aceeași lățime (egală cu lățimea drumului) și lungimi numere naturale. Fiind un împărat cam sâcâit, acesta dorește ca pavarea să se facă folosind un număr minim de dale, diferența de lungime între două dale vecine să nu fie mai mare ca 1, iar prima și ultima dală să fie de lungime 1. Împăratul nu se mulțumește să primească de la Făt-Frumos doar un număr (numărul minim de dale necesare): el vrea și posibilitatea de pavare cea mai mică din punct de vedere lexicografic.
Cunoscând lungimea drumului, determinați numărul minim de dale necesare pavării și posibilitatea de pavare cu număr minim de dale, care este cea mai mică din punct de vedere lexicografic.
OJI 2015, Clasa a VIII-a
- Fișiere
- Daniel Popa
- concurs
- Clasa 9 Probleme diverse Probleme diverse
#1137
Cuart
Gina şi Mihai joacă împreună jocul Cuart. Ei au la dispoziție un șir de 2*N cartonașe ce conțin numere naturale. Primele N cartonașe, de la stânga la dreapta, sunt ale Ginei, iar următoarele N ale lui Mihai. Gina traversează șirul, de la stânga la dreapta și scrie pe o foaie de hârtie, pe primul rând, un șir de numere obținut din numerele de pe cartonașele sale, din care a șters toate cifrele pare. La fel procedează Mihai care scrie pe foaia sa de hârtie, pe primul rând, șirul de numere obținut din numerele de pe cartonașele sale, din care a șters toate cifrele impare. Dacă dintr-un număr s-au șters toate cifrele, sau au rămas doar cifre egale cu 0, atunci numărul este ignorat, deci pe hârtie nu se scrie nimic.
Fiecare copil, notează pe hârtia sa, pe al doilea rând, un alt șir de numere obținut astfel: pentru fiecare număr X scris pe primul rând, copilul va scrie cel mai mare număr natural K cu proprietatea că 1+5+9+13+...+ K ≤ X. În jocul copiilor, numărul X se numește cuarț dacă 1+5+9+13+...+K = X.

În exemplul de mai sus, Gina nu a scris niciun număr cuarț pe primul rând, iar Mihai a scris unul singur (6=1+5).
Regulile de câștig ale jocului sunt următoarele:
- Câștigă acel copil care are scrise pe primul rând cele mai multe numere cuarț. În acest caz, valoarea de câștig a jocului este egală cu numărul de numere cuarț scrise de copilul câștigător.
- Dacă cei doi copii au scris același număr de numere cuarț, atunci va câștiga cel care are primul număr scris pe primul rând, mai mare decât al celuilalt. Acest prim număr scris de câștigător va reprezenta valoarea de câștig.
- Dacă nici Gina și nici Mihai nu au scris niciun număr pe hârtie, se consideră egalitate și nu câștigă niciunul.
Scrieţi un program care să citească numărul N reprezentând numărul de cartonașe ale unui copil şi cele 2*N numere de pe cartonașe, în ordine de la stânga la dreapta și care să determine:
1) Cel mai mare număr de pe cele 2*N catonașe, pentru care nu s-a scris niciun număr pe primul rând (a fost omis), nici pe hârtia Ginei, nici pe hârtia lui Mihai; dacă nu a fost omis niciun număr, se va scrie 0;
2) Câștigătorul jocului și afișează numărul 1 dacă a câștigat Gina, 2 pentru Mihai sau 0 în caz de egalitate.
3) Valoarea de câștig a jocului, sau 0, în caz de egalitate.
OJI 2015, Clasa a V-a
- Fișiere
- concurs
- Clasa 9 Algoritmi elementari Cifrele unui număr
#1138
Speciale
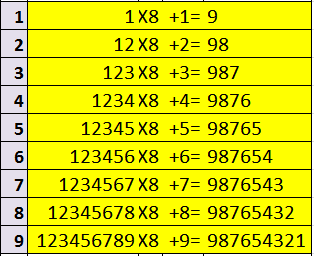 Maria a aflat că numerele naturale care încep cu cifra
Maria a aflat că numerele naturale care încep cu cifra 1 și au toate cifrele ordonate strict crescător şi consecutive sau încep cu cifra 9 și au toate cifrele ordonate strict descrescător şi consecutive se numesc numere speciale. Interesată să descopere legătura dintre numerele speciale cu același număr de cifre, a observat că poate construi tabelul alăturat.
Scrieţi un program care citind patru numere naturale K, N, A şi B determină:
1) cel mai mare număr special situat în tabel pe linia K;
2) numărul special obţinut din numărul N prin ştergerea unei cifre;
3) numărul de numere speciale din mulțimea {A , A +1, A+2, A+3…,B-1,B}.
OJI 2015, Clasa a V-a
- Fișiere
- concurs
- Clasa 9 Algoritmi elementari Cifrele unui număr
#1141
ech
Numim număr echilibrat un număr natural pentru care suma cifrelor de pe poziţii pare este egală cu suma cifrelor de pe poziţii impare.
De exemplu numărul 13552 este echilibrat, pentru că 1+5+2=8=3+5.
Dat fiind un număr natural N să se determine cel mai mic număr echilibrat, strict mai mare decât N.
OJI 2015, Clasa a VII-a
- Fișiere
- Emanuela Cerchez
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme diverse
- Numere mari
#1143
Dominant
Considerând un șir de valori binare, numim secvență dominantă un set de elemente aflate pe poziții consecutive în șir care are proprietatea că numărul valorilor egale cu 1 este strict mai mare decât numărul valorilor de 0. De exemplu, în șirul 1,0,0,0,1,1,0,1,1,1,0,0 o secvență dominantă este 0,1,1 și o alta, de lungime mai mare, este 0,1,1,0,1,1,1. Secvența dominantă maximală este secvența dominantă de lungime maximă. În șirul din exemplu secvența dominantă maximală este 1,0,0,0,1,1,0,1,1,1,0 (adică întreg șirul, fără ultimul zero).
Dat fiind un șir de valori binare, să se determine lungimea unei secvențe dominante maximale precum și numărul acestor secvențe.
OJI 2015, Clasa a VIII-a
- Fișiere
- Dan Pracsiu
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme diverse